レトラクションの起源（かな？）

レトラクション（retraction）やベキ等自己射（idempotent endomorphism）の典型例つうか起源は、図形の引き込み変形のような気がします。いやっ、気がするだけでほんとのところは知らないけど。まーとにかく、絵を描いておきます。

平面をPとして、普通の座標を入れてR²と同一視しておきます。D = {(x, y)∈P | x² + x² ≦ 1}は円板。Pの部分集合である円板Dはそのままにして、円板の外側を境界円周に押し込めるような変形（連続写像）を作ります。

円周を“折り目”として、円板の外側を持ち上げて、最終的に底面付きの円筒を作ります。平面における放射状の半直線達が、円筒の柱面（まるい側面）を構成します。円筒を真上からドガッベシャッ！とつぶします。

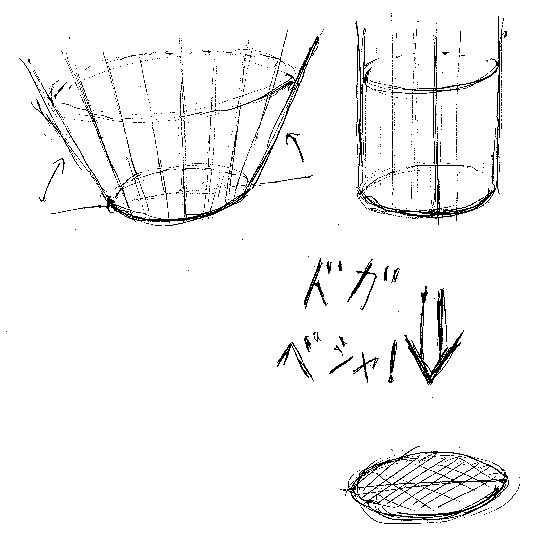
以上の操作（連続写像）を、P→Dと考えたものをr1, P→Pと考えたものをr2、またD→Pの包含写像をiとすると：

• i;r1 = id_D （レトラクト性）
• r1;i = r2
• r2;r2 = id_P r2（ベキ等性）

などが成立します。

連続性が必要ないならもっと簡単で、Dの任意の一点（例えば原点）を選んで、Dの外側は全部その一点に写してしまう（1点に引き込む）写像が使えます。これは一点レトラクトで、やはりレトラクト性やベキ等性が成立します。