絵図的手法とは、視覚化可能な組み合わせ構造〈visualizable combinatorial structure〉を使って代数系や現実のシステムを記述・計算する方法・技術です。視覚化可能な組み合わせ構造の重要な種別として半グラフ〈semi-graph〉があります。半グラフは1次元の図形でした。2次元の図形で表現可能な視覚化可能な組み合わせ構造について考えてみます。それは、バエズ/ドーラン・ツリーの一般化なので、バエズ/ドーラン植物〈Baez-Dolan plant〉と呼ぶことにします(木は植物の一種)。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\pipe}{\mid }
\newcommand{\ccol}[1]{\boldsymbol{#1} }
%\newcommand{\msf}[1]{\mathsf{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{-} }
\newcommand{\op}{\mathrm{op} }
%\newcommand{\id}{\mathrm{id} }
%\newcommand{\pto}{ \supseteq\!\to }
\newcommand{\u}[1]{\underline{#1}}
\newcommand{\cpal}[1]{\mathfrak{#1} }
%\newcommand{\msc}[1]{\mathscr{#1}}
\newcommand{\bdry}{\partial}
`$
内容:
曲面の穴ってなに?
閉曲面について考えます。ここでの閉曲面〈closed surface〉とは、コンパクトで境界を持たない連結向き付け可能2次元多様体のことです*1。例えば、以下の2つの図形は閉曲面です。
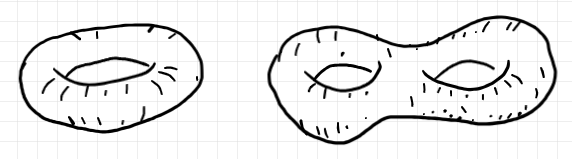
左側はトーラスで、ドーナッツ、あるいは浮き輪の表面です。右側は二人乗りの浮き輪です。トーラスには穴がひとつ、二人乗り浮き輪には穴がふたつあります。今言った「穴」は、閉曲面の形状の特徴としての穴です。
「穴」という言葉のもうひとつの用法として、曲面の一部をくり抜いた跡の空洞を意味することがあります。例えば、以下の曲面は(もはや閉曲面ではないが*2)ひとつ穴のトーラスにふたつの“穴”を穿〈うが〉ったものです。トーラスの内部(裏側)は赤い色で、それが穴から見えているという設定です(かえって分かりにくかったか?)。

「穴」の用法がたいへんに紛らわしいですね。閉曲面の特徴としての穴の個数は種数〈genus〉と呼んで、以下では穴には直接言及せずに「種数 $`g`$ の閉曲面」という言い方をすることにします。
曲面〈2次元多様体〉に穴を穿つとはどういうことかを述べましょう; $`M`$ を、コンパクトとは限らず境界を持つかも知れず連結とは限らない2次元多様体だとします。$`M`$ の開集合 $`H`$ が開円板となめらかに同相だとします。このとき、$`M \setminus H`$ を作ることが穴を穿つことです。穴を穿つ、つまり $`H`$ をくり抜くと、くり抜いた跡に、円周 $`S^1`$ となめらかに同相な境界成分が生まれます。
我々がこれから扱う図形は、種数 $`g`$ の閉曲面に、何個か(0個でもよい)の穴を穿った穴あき曲面です。この種の穴あき曲面は、コンパクトで境界を持つかも知れず連結な向き付け可能2次元多様体です。以下では、穴の個数を $`N`$ として、種数 $`g`$ の $`N`$-穴あき曲面〈genus $`g`$ surface with N-holes | N-punctured surface of genus $`g`$〉と呼びます。$`N = 0`$ のときが種数 $`g`$ の閉曲面です。
バエズ/ドーラン・ツリー
バエズ/ドーラン・ツリー〈Baez-Dolan tree〉については、「入れ子の半グラフとバエズ/ドーラン・ツリー」で述べています。以下はバエズ/ドーラン・ツリーの一例です(「入れ子の半グラフとバエズ/ドーラン・ツリー」から再掲)。
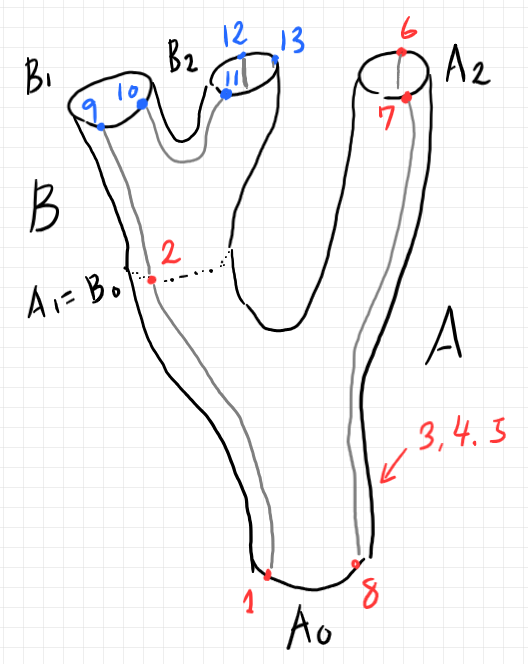
バエズ/ドーラン・ツリーには、色々なラベルが付けられて模様が描かれていますが、ラベル・模様を取り去ると曲面〈2次元多様体〉になります。上の絵では、ツリーらしく描いていますが、位相的性質を変えない変形をほどこすと、バエズ/ドーラン・ツリー(の曲面)は、球面に(n + 1)個の穴を開けた図形だとみなせます。n はルート以外の穴の個数です。
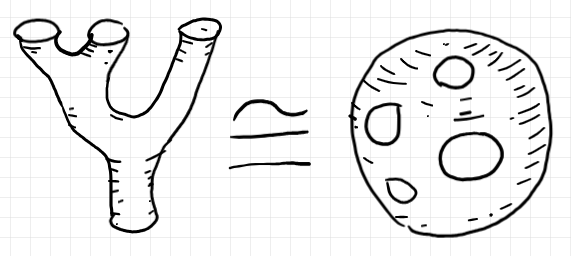
バエズ/ドーラン・ツリーの絵を描くときは、引き続きツリーっぽく描きますが、穴あき球面として描いてもかまいません。バエズ/ドーラン・ツリーの土台となっている穴あき球面と同相な曲面をバエズ/ドーラン・ツリーの輪郭〈コントゥア | conture〉と呼ぶことにします。バエズ/ドーラン・ツリーの輪郭の位相的特徴は穴の数だけで記述できます。
バエズ/ドーラン・ツリーは、輪郭の曲面だけではなくて、曲面に付加された構造を持っています。それらは:
- 境界装飾〈boundary decoration〉
- 境界成分の番号〈number〉
- 境界成分のプロファイル〈profile〉
- ルート以外の境界成分の値〈value〉
- ワイヤリング〈wiring〉
これらについて、幾何的・位相的に説明します。実際に必要なのは、幾何的・位相的な定義から抽出される組み合わせ的・代数的構造です。しかし、導入としては幾何的・位相的な定義のほうがわかりやすく直感的だと思います。
境界に装飾を付ける
$`M`$ は、球面に(n + 1)個の穴をあけた曲面とします。曲面の境界を $`\bdry M`$ とします。$`\bdry M`$ は、(n + 1)個の円周($`S^1`$ と書く)の直和と同相になります。
$`\quad \bdry M \cong S^1 \coprod S^1 \coprod \cdots \coprod S^1`$
境界の連結成分は円周なので、それぞれの連結成分を境界円周〈boundary circle〉とも呼びます。
穴あき曲面をバエズ/ドーラン・ツリーに仕立てる最初の作業は、境界円周に番号をふること〈numbering〉です。番号は、$`0`$ から $`n`$ の自然数を使います。ツリーのルートとして特定される境界円周には番号 $`0`$ を割り当てます。その他の境界円周には $`1`$ から $`n`$ の番号をふります。
番号 $`i`$ で識別される境界円周を $`(\bdry M)_i`$ または $`\bdry_i M`$ と書くことにします。後者の書き方をすると、$`\bdry_i`$ が、$`i`$番目の境界円周を取り出す作用素の意味になります。この書き方を使うと、次が成立します。
$`\quad \bdry M = (\bdry M)_0 \coprod (\bdry M)_1 \coprod \cdots \coprod (\bdry M)_n\\
\quad \bdry M = \bdry_0 M \coprod \bdry_1 M \coprod \cdots \coprod \bdry_n M\\
\quad \forall i\in \{0, 1, \cdots, n\}. (\bdry M)_i = \bdry_i M \cong S^1
`$
次に境界円周にプロファイルを割り当てます。プロファイルとは、色付きコレクションのことです。色付きコレクションについては次の記事に書いています。
境界円周に色付きコレクションを割り当てる話の詳細は組み合わせ的議論になるので、ここでは、幾何的におおざっぱな説明をします; ひとつの境界円周に対して、有限個(0個でもよい)の境界円周上の点を選びます。選んだ点はポート点〈port point〉、または単にポート〈port〉と呼びます。ポート点には“色”と呼ばれる値を割り当てます。“色”は日常語ではなくてテクニカルタームです(「コレクション、対称性、シーケンス、色付け」参照)。今は、色がなんであるかは気にしなくていいです。すべての境界円周に対して、その上のポート点を決めて色付け〈coloring〉します。これで、プロファイルの割り当ては終了です。
境界修飾の最後の作業として、ルート(0番の境界円周)以外の境界円周に“値”を割り当てます。“値”がなんであるかも、今はどうでもいいです。何らかの集合からn個の要素をとってきて $`v_1, v_2, \cdots, v_n`$ とします。$`v_i`$ が 境界円周 $`\bdry_i M`$ に割り当てる“値”です。
この後で必要となるのは、境界円周の番号とポート点達です。ポート点の“色”と境界円周の“値”は、幾何的な説明には使いません(組み合わせ的には重要ですが)。
バエズ/ドーラン・ツリーを $`T`$ としたとき、次の記法を使います。
- $`T`$ の輪郭〈コントゥア〉を、$`\mrm{Conture}(T)`$ と書く。しばしば、$`M := \mrm{Conture}(T)`$ のように置く。
- $`T`$ のポート点達の集合を、$`\mrm{Port}(T)`$ と書く。$`\mrm{Port}(T) \subseteq \bdry \mrm{Conture}(T)`$ 。
ワイヤリング
バエズ/ドーラン・ツリーにおけるワイヤリングとは、ポート点たちを線で結ぶことです。バエズ/ドーラン・ツリーの輪郭〈コントゥア〉である曲面 $`M`$ 上に、ワイヤーが描かれることになります。
$`[0, 1]\subset {\bf R}`$ は単位閉区間とします。単位閉区間の$`L`$個の直和を次のように書きます。
$`\quad L\cdot [0, 1] := [0, 1] \coprod \cdots \coprod [0, 1]`$
便宜上、各単位閉区間に番号をふるとして、次のように書きます。
$`\quad L\cdot [0, 1] = [0, 1]_1 \coprod \cdots \coprod [0, 1]_L`$
$`{\bf 1}`$ を単元集合(一点からなる図形)として、境界に関して次が成立します。
$`\quad \bdry L\cdot [0,1] \cong 2L\cdot {\bf 1}`$
$`L`$個の単位閉区間の境界は$`2L`$個の点だ、と言っているだけですから当たり前です。$`\bdry L\cdot [0,1]`$ の$`2L`$個の点も枝番方式で次のように表すことにします。
$`\quad 1.0, 1.1, 2.0, 2.1, \cdots L.0, L.1`$
輪郭が $`M`$ であるバエズ/ドーラン・ツリー $`T`$ におけるワイヤリング〈wiring〉は、次のようななめらかな写像です。ただし、色々と条件は付きます。
$`\quad w : L\cdot[0, 1] \to M`$
$`w`$ に関する条件を述べていきます。まず、$`w`$ は境界点達とポート点達の一対一対応を与えます。
- $`w(\bdry L.[0, 1]) \subseteq \mrm{Port}(T)`$
- $`w`$ を $`{\bdry L.[0, 1]}`$ と $`\mrm{Port}(M)`$ に制限した写像を $`w'`$ とすると、$`w': \bdry L.[0, 1] \to \mrm{Port}(T)`$ は同型射〈双射 | 全単射〉となる。
同型射 $`w'`$ を通じて、ポート達にも枝番方式の番号 $`j.\alpha`$ を付けられます。これは:
- $`j = 1, 2, \cdots, L`$
- $`\alpha = 0, 1`$
- $`j.0`$ は、$`j`$番目のワイヤーの始点であるポート点。$`j.1`$ は、$`j`$番目のワイヤーの終点であるポート点。
なんだか面倒な話ですが、目視・直感的には「目に見えているアレ・コレ」に、すべて番号や名前を付ける必要があるのです。
まだ条件はあります。$`w`$ は、各単位閉区間ごとに単射だとします。$`w`$ を$`j`$番目の単位閉区間 $`[0, 1]_j`$ に制限した写像を $`w_j`$ と書くことにすると:
- $`w_j : [0, 1]_j \to M`$ は単射。
$`w`$ 全体で単射であることは要求しません。単射でなくなっているような点はあるかも知れません。つまり、次の命題が真になる可能性があります。
$`\quad \exists x, y \in L\cdot [0, 1].\, w(x) = w(y)`$
$`w(x) = w(y)`$ であるような $`x, y\in L\cdot [0, 1]`$ は、$`w(x) \in M`$ で交差している〈crossing〉といいます。
交差している二点 $`x, y,\, w(x) = w(y)`$ 、 あるいは三点 $`x, y,z\,\, w(x) = w(y) = w(z)`$ などがあってもかまいまんせんが、交差している点達は有限個しかないことは要求します。無限個の点達がベタッとくっついてしまうのはダメです。
交差は、ワイヤリングの写像 $`w`$ を“変形”して解消できることもあります。いくら頑張っても消せない交差もあります(下図)。この話題は難しいことなのでこれ以上は深入りしません。
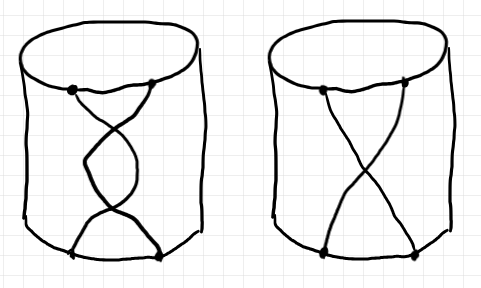
最初から、全体として単射であるワイヤリング $`w`$ を考えることにすると悩みは少なくなります(一般性は失われますが)。
逆向きのワイヤー
$`T`$ は輪郭が $`M`$ であるバエズ/ドーラン・ツリーだとします。$`w: L\cdot [0, 1] \to M`$ は$`T`$ のワイヤリングとします。ワイヤリングも $`T`$ が持つ構造の一部です。$`w`$ を $`[0, 1]_j`$($`j = 1, 2, \cdots L`$)に制限した写像を $`w_j : [0, 1]_j \to M`$ とします。各 $`w_j`$ をバエズ/ドーラン・ツリー $`T`$ のワイヤーと呼びます。定義から、(今のところ)$`L`$本のワイヤーがあります。
$`w_j:[0, 1]_j \to M`$ に対して、次のような写像を考えます。(変数 $`t`$ は閉区間 [0, 1] 内を走るとしてます)
$`\quad t \mapsto w_j(1 - t) \in M`$
こうやって作った写像を(ちょっと紛らわし記法ですが)$`-w_j`$ と書きます。$`-w_j`$ は $`w_j`$ とは逆向きなワイヤーになります。もとのワイヤーの否定〈negation〉とも呼びます。すべてのワイヤー $`w_j`$ に対してその否定 $`-w_j`$ を作ると、ワイヤーの本数はニ倍になります。
$`\quad w_1, w_2, \cdots, w_L, -w_1, -w_2, \cdots, -w_L`$
これら$`2L`$本のワイヤーを要素とする集合を $`\mrm{Wire}(T)`$ とします。集合 $`\mrm{Wire}(T)`$ は有限集合でその基数は $`2L`$ です。$`\mrm{Wire}(T)`$ は単なる有限集合ではなくて、次の対合〈involution〉を持ちます。
$`\quad w_j\mapsto -w_j`$
つまり、$`(\mrm{Wire}(T), -)`$ は不動点を持たない対合付き集合となります。半グラフとの関係性が匂ってきます(例えば、「テンソルの可視化のための半グラフ」参照)。
ワイヤーには始点〈ソース点〉と終点〈ターゲット点〉があるので、ワイヤーに始点/終点を対応させる写像もあります。
$`\quad \mrm{src} : \mrm{Wire}(T) \to \mrm{Port}(T)\\
\quad \mrm{trg} : \mrm{Wire}(T) \to \mrm{Port}(T)
`$
有限集合のあいだの写像 $`\mrm{src}, \mrm{trg}`$ も組み合わせ構造を作るときに使えます。
例外ループ
このプログ内の過去記事で、半グラフの無頂点ループを「サークル」とも呼んできました(例えば、「サークルを持つ半グラフ」参照)。しかし、バエズ/ドーラン/ツリーの境界もサークル〈円周〉なので混乱しそう。無頂点ループ〈loop with no vertices | nodeless loop | free floating loop〉をサークルと呼ぶのはやめます。レイノア〈Sophie Raynor〉が使っていた用語「例外ループ〈exceptional loop〉」を使うことにします。
特殊なワイヤーとして例外ループを認める場合は、ワイヤリング写像 $`w`$ の域〈domain〉を次の形にします。
$`\quad L\cdot [0, 1] \coprod K\cdot S^1`$
$`K`$ は域内の円周の個数です。$`K = 0`$ なら例外ループはありません。域内の円周にも $`1, \cdots, K`$ で番号を付けることにします。すると、ワイヤリング写像 $`w`$ の域は次のように書けます。
$`\quad [0, 1]_1 \coprod \cdots \coprod [0, 1]_L \coprod S^1_1 \coprod \cdots \coprod S^1_K`$
円周 $`S^1_k`$ に制限した $`w`$ を次のように書きます。これが一本の例外ループです。
$`\quad w_{\hat{k}} : S^1_k \to M`$
円周 $`S^1_k`$ に境界はないので、$`w_{\hat{k}}`$ の像は $`M`$ の境界と交わることはありません。$`w_{\hat{k}}`$ にも前節の条件は適用されて、単射でなくてはなりません。$`w`$ 全体としての交差により、他のワイヤーと例外ループが交差することはあるかも知れません。
例外ループ $`w_{\hat{k}}`$ もワイヤーの一種なので、逆向きの例外ループ〈否定〉 $`-w_{\hat{k}}`$ を考えることができます。前節と同様な手順で、すべてのワイヤー(例外ループも含める)の逆向きのワイヤー〈否定〉を作ると、例外ループも含めて $`2L + 2K`$ 本のワイヤーの集合ができます。この集合も不動点を持たない対合付き集合です。両端を持つ普通のワイヤー〈normal wire〉とは違い、例外ループに対して $`\mrm{src}, \mrm{trg}`$ は定義できません。
バエズ/ドーラン・ツリー $`T`$ に対して、例外ループも含めて、逆向きのワイヤーも入れたすべてのワイヤーの集合を引き続き $`\mrm{Wire}(T)`$ と書きます。例外ループの集合は $`\mrm{Except}(T)`$ です。すると、$`\mrm{src}, \mrm{trg}`$ のプロファイルは次のようになります。
$`\quad \mrm{src}, \mrm{trg} : (\mrm{Wire}(T) \setminus \mrm{Except}(T)) \to \mrm{Port}(T)`$
例外ループは扱いが難しいので、例外ループを禁止する場合も多くあります。が、一般論を展開するときは例外ループも許容しないと適用範囲を狭めてしまいます。
バエズ/ドーラン・ツリーの円板表示
「入れ子の半グラフとバエズ/ドーラン・ツリー」において、もともと穴あき円板〈{disk | disc} with holes*3〉内のワイヤリング図を変形して3次元ツリーの形状に描き直しました。つまり、バエズ/ドーラン・ツリーは、穴あき円板を輪郭(あるいはキャンバス)にしても描けるわけです。
以下の絵は、ダンクソ/ハラーチェバ/ロバーツォンの論文 [DHR20] の FIGURE 1 の画像コピーです。穴あき円板をキャンバスとして描いたワイヤリング図です。
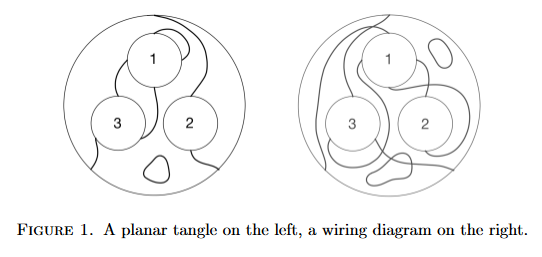
- [DHR20]
- Title: Circuit algebras are wheeled props
- Authors: Zsuzsanna Dancso, Iva Halacheva, Marcy Robertson
- Submitted: 21 Sep 2020
- Pages: 29p
- URL: https://arxiv.org/abs/2009.09738
外の円周は番号 0 です(書いてないけど)。左側は交差を許さないワイヤリング、右側は交差を許すワイヤリングです。例外ループも許しています。
穴あき円板なら2次元の図として描けるので、幹や枝がパイプである3次元ツリーを立体的に描くより楽です。この描き方を、バエズ/ドーラン・ツリーの円板表示〈{disk | disc} presentation〉と呼ぶことにします。輪郭を2次元平面内の領域として表示する方法です。
円板表示は便利ですが、ツリー〈木〉としての描画が役立つ場面もあるので、パイプ・ツリーとしての表示も併用します。
バエズ/ドーラン植物
バエズ/ドーラン植物〈Baez-Dolan plant〉は、バエズ/ドーラン・ツリーの一般化です。一般化する点は:
- 穴をあける前の輪郭曲面として(球面に限らず)種数 $`g`$ の閉曲面を使ってよい。したがって、輪郭は種数 $`g`$ の穴あき曲面になる。
- 境界円周(穴の縁〈ふち〉)に符号〈sign〉を付ける。
以下は、種数 1 のバエズ/ドーラン植物の例です。
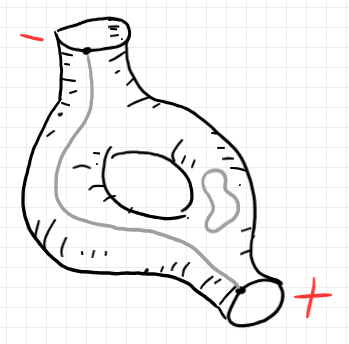
ワイヤーはグレーで描いています。普通のワイヤー〈normal wire〉が1本と例外ループ〈exceptional loop〉がひとつです。赤で書いた +, - が符号です。符号には 0 もあり、各境界円周に $`\{+, -, 0\}`$ の要素を割り当てます。色付け〈プロファイル付け〉と値割り当ては明示的には描いてません。
種数 0 のバエズ/ドーラン植物がバエズ/ドーラン・ツリーです。種数 1 のバエズ/ドーラン植物は、円板表示では描けなくなります。輪郭曲面を切り分けて幾つかの円板で描く方法はあります。
種数が 1 以上のバエズ/ドーラン植物(ツリーではない植物)は必要でしょうか? コピーを表す分岐パイプ〈forked pipe〉と何らかの二項演算を表す合流パイプ〈joined pipe〉を繋ぐと、種数 1 の輪郭曲面が生じます。曲面の特徴としての“穴”(この記事の最初の節参照)が自動的に潰れるならいいのですが、一般的には穴あき球面ではない曲面(種数 ≧ 1)も扱うことになります。
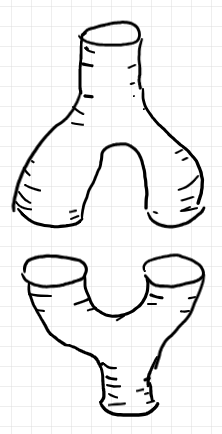
この記事では、バエズ/ドーラン・ツリーとその一般化であるバエズ/ドーラン植物を幾何的に導入しましたが、絵図的手法では、幾何的な事物から抽出した組み合わせ的情報も扱います。幾何的記述は、目視可能で直感的であるメリットがありますが、組み合わせ的記述に置き換えると機械的な計算が可能となるメリットがあります。
バエズ/ドーラン植物の、組み合わせ的・代数的議論はまたいずれ。