一昨日の記事「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」でオペラッドの話をしたので、小円板オペラッド〈little disks operad〉における計算を型付きラムダ計算のフレームワークに乗せてみましょう。これによって、オペラッドの計算論的側面が見えてきたり、ラムダ計算の適用範囲の広さを実感できたりします。
内容:
小円板キャンバスと平面タングル
小円板オペラッドのオペレータは、円板から何個か(0個でもよい)の小円板をくり抜いた図形でした(一昨日の「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」参照)。つまり、小円板オペレータは穴あき円板です。穴が1個のときは円環〈annulus〉、穴が0個のときはソリッドな円板〈solid disk〉(SSDのことじゃない)です。
この記事では「オペレータ」を使ってますが、「オペレーション」が多いようです。修正はしませんが、「オペレーション」が一般的な用語だと注記しておきます。
[/追記] [/補足]
のっぺらぼうの穴あき円板では味気ないので、板に模様〈絵柄〉が描かれているとしましょう。この模様とはストリング図ですが、具体的にどんなストリング図が描かれているかは気にしないで、「なんらかのストリング図か描かれている」という想定です。
“模様=ストリング図”が描かれる前の穴あき円板を小円板キャンバス〈little disks canvas〉、混乱の恐れがなければ単にキャンバス〈canvas〉と呼びます。
小円板キャンバスの外側の円周を外円周〈outer circle〉、穴の周囲の円周を内円周〈inner circle〉と呼ぶことにします。キャンバスに空いている穴は、番号で識別できますが、名前を付けてもいいとします。内円周を識別するための番号や名前を総称してラベル〈label〉といいます*1。“ラベルの選択=穴/内円周への命名”は根拠なき選択です。
外円周にも内円周にも基準点〈base point〉が必要です。基準点は、“オペラッド結合=はめ込み”のときの位置合わせに使います。基準点について詳しくは次の記事を参照してください。
キャンバスの構造を絵にまとめると次のようです。基準点は円周上にアスタリスクで描いています。
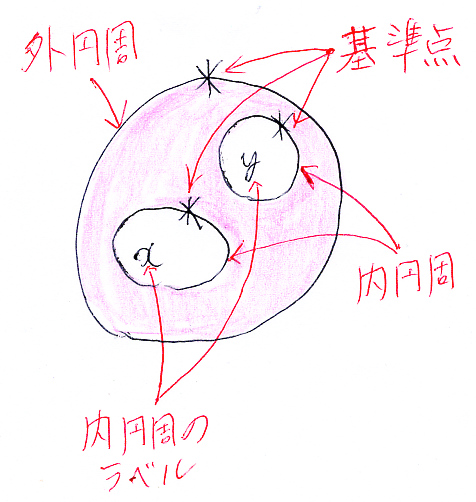
キャンバスに“模様=ストリング図”を描いた“模様付き穴あき円板”は、ジョーンズ等にしたがい平面タングル〈planar tangle〉と呼びましょう。ただし、領域の塗り分け〈色付け〉はしません。模様は線と点だけで構成されています。
平面タングルと「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」のストリング図テンプレートはほとんど同じです。円板を使うか四角形(2次元方体)を使うかの違いがあるだけです。つまり、“ここでの平面タングル=円板ベースのストリング図テンプレート”です。
ラムダ計算の基本
ラムダ計算の基本的な事項を、JavaScriptや絵を使って非形式的に説明した入門的記事に以下があります。ラムダ計算をまったく知らない方は読んでおくといいかも知れません。
ラムダ項(ラムダ計算で使う式・表現)の例として、定数、変数、足し算と掛け算を含むような項を考えてみましょう。例えば、x2 + 1 とか xy + 2y とか x + y とか 3×5 + 2×7 + 1 とかです。項 E に出現する変数の集合を Var[E] と書きます。Var[x2 + 1] = {x}, Var[xy + 2y] = {x, y}, Var[x + y] = {x, y}, Var[3×5 + 2×7 + 1] = {} とか。
各変数が1回だけ出現する項を(ここだけの言葉で)単純項〈simple term〉と呼びましょう。x2 + 1 は x×x + 1 の略記なので、x が2回出現していて単純項ではありません。xy + 2y には y が2回出現するので単純項じゃありません。x + y は単純項です。3×5 + 2×7 + 1 は変数を含まないので単純項とみなします*2。
ラムダ計算の項は、λx.(x2 + 1) のように、先頭に'λ'が付くラムダ抽象項(関数を意味する)があります。与えられた項 E から λx.E を作ることがラムダ抽象〈lambda abstraction〉です。記号'λ'の直後の変数をラムダ変数〈lambda variable〉と呼びます。ラムダ変数は、関数の引数変数〈argument variable〉と思えばいいです。λx.(λy.E) のように、ラムダ抽象を入れ子にすることもできます。ラムダ変数は、普通の変数〈自由変数〉から除外されるので、Var[λx.(x2 + 1)] = {}, Var[λy.(xy + 2y)] = {x}, Var[λx.(λy.(xy + 2y))] = {} です。
関数に引数を渡すことを表す適用〈application〉の中置演算子記号として、'・'を使います。(λx.(x2 + 1))・(s + t) とか (λx.((λy.(xy + 2y))・(s + t)))・10 とかが、'・'を使った項の例です。これらは次のように“計算”されます。
(λx.(x2 + 1))・(s + t) = (s + t)2 + 1 (λx.((λy.(xy + 2y))・(s + t)))・10 = (λx.(x(s + t) + 2(s + t)))・10 = 10(s + t) + 2(s + t))
普通の代入計算ですね。
ラムダ項としての平面タングル
次のような平面タングル S を考えます。これは、前々節のキャンバスにストリング図を描いたものです。
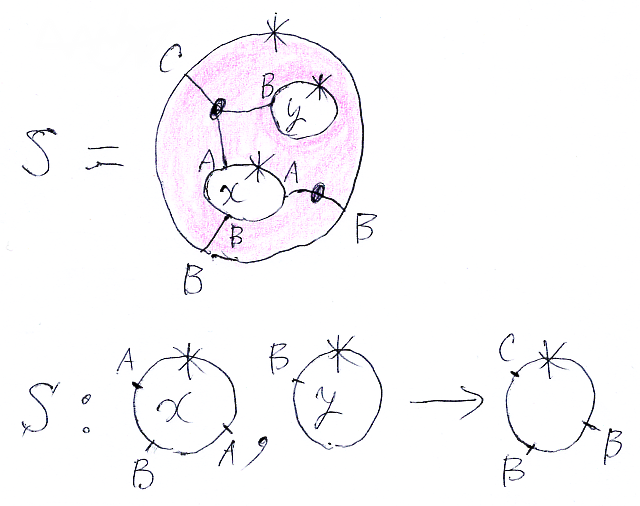
この平面タングルにおいて、x, y は穴(あるいは内円周)のラベル、A, B, C はストリング図のワイヤーのラベルです。内円周が入力、外円周が出力と考えて、平面タングルのプロファイル〈profile〉を次の形に書きます。
- 内円周達をカンマで区切ったリスト → 外円周
穴がない平面タングルの場合は、矢印の左側は空リストになります。
ここから先、「円周」といった場合、単なる平面図形ではなくて、基準点(アスタリスク)と、ワイヤーのラベル(A, B, C など)が付いた点まで含めた構造を意味します*3。基準点は常にありますが、ラベルされた点はないときもあります。
プロファイルをテキストで書くために、円周を基準点から反時計回りに見て、出現するワイヤー・ラベルを並べることにします。上の図では絵で描いたプロファイルをテキストで書けば:
- S: x:(A, B, A), y:(B) → (C, B, B)
平面タングル S を、変数 x, y を含む項と考えて、ラムダ抽象や適用を考えます。次の対応を念頭におきます。
| 平面タングル | 単純項 |
| 穴(内円周)のラベル | 変数 |
| 円周 | 変数の型 |
| オペラッド結合 | ベータ変換(後述) |
平面タングルの穴のラベルは、同じラベルは1回しか出現しないので単純項に対応します。円周は、穴のラベルに対する型だと考えます。変数(穴のラベル)に型(円周)が付いているので、平面タングルの計算は型付きラムダ計算になります。
平面タングルのラムダ抽象と適用
平面タングル X に対して、穴のラベルの集合を Label(X) と書きます。前節の平面タングル S ならば、Label(S) = {x, y} です。これは、項 E に対する変数の集合 Var(E) と事実上同じものです(呼び名が違うだけ)。平面タングルの穴ラベルを選んで、そのラベルに関するラムダ抽象が行えます。ただし、出現してないラベルに関するラムダ抽象(空虚なラムダ抽象〈vacuous lambda abstraction〉という)は禁止します*4。
平面タングル X のラムダ抽象〈lambda abstraction〉は、ξ∈Label(X) に対して λξ:Φ.X の形で書きます。ここで、Φはラベルξの型である円周です。一般的な記述をするために、メタ変数 'ξ', 'Φ' を使ったのですが、具体例 S に関して言えば、λy:(A, B, A).S が、ラベル y に関する S のラムダ抽象です。
ラムダ抽象した平面タングルを絵だけで描きたいときは、ラムダ抽象に使ったラベルと対応する内円周に何らかの修飾を施します。例えば、色を赤くして、ラベルにハットを付けます。
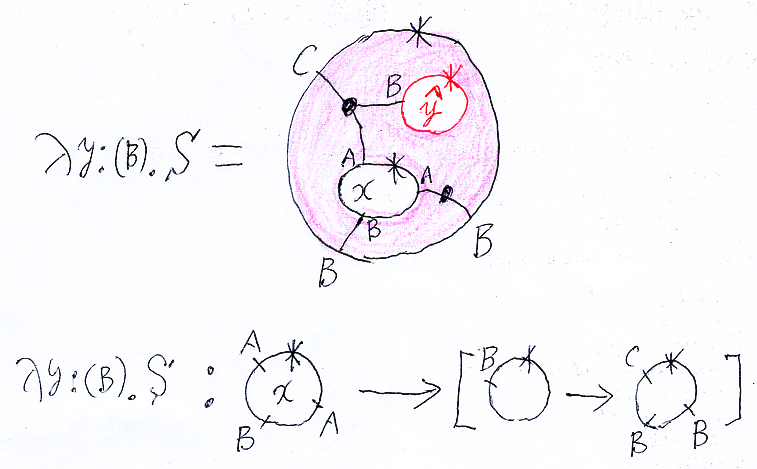
色を変えるまでするのは実際上は面倒なので、ラベルにハットだけでもいいでしょう。いずれにしても、ラムダ・ラベル〈lambda label〉(ラムダ抽象に使われたラベル)を識別するマークを付けます。
ラムダ抽象した平面タングルのプロファイルは x:(A, B, A)→[(B)→(C, B, B)] のようになります。ここで、[(B)→(C, B, B)] は、通常、高階型/関数型/指数型/内部ホム型 などと呼ばれている型ですが、「(B)型の平面タングルをを受け取って、(C, B, B)型の平面タングルを返すもの」の型です。今は、キャンバスに描くストリング図の詳細を決めてないので、[(B)→(C, B, B)] の意味を正確に記述できないのですが、直感的にはだいたい分かるでしょう。
平面タングル X をラムダ抽象すると、使ったラベル(ラムダ・ラベル)はラベルの集合 Label(X) から除外されます。例えば、Lable(λy:(B).S) = {x} です。ラムダ・ラベルは外から見えなくなるので、自由にリネームできます*5。例えば、y を z にリネームしてもかまいません。ラムダ・ラベルのリネームをアルファ変換〈alpha conversion〉と呼びます。ラムダ計算の習慣により、互いにアルファ変換で移りあえる2つの平面タングルは同一視します。
次に適用の話をします; 適用を表す記号は'・'を使うとして、例えば、次の形で使います。
- (λy:(B).S)・T
T は具体的に次の平面タングルだとしましょう。
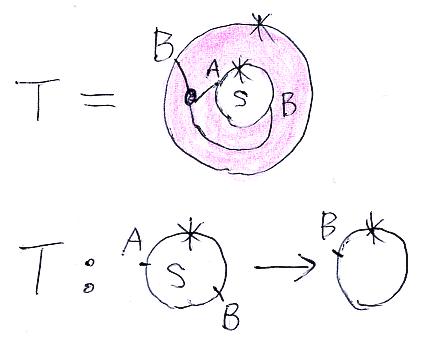
このとき、(λy:(B).S)・T は次の公式で“計算”します。
- (λy:(B).S)・T = S
T
右辺はオペラッド結合で、その結果は次の図のようになります。
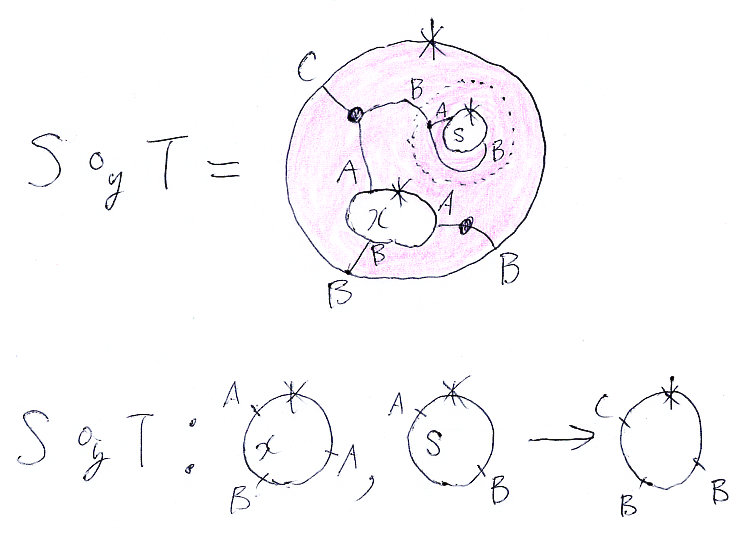
ラムダ計算では、適用を含む形 (λy:(B).S)・T から ST に変形する操作をベータ変換〈beta conversion | beta reduction〉と呼びます。平面タングルのラムダ計算におけるベータ変換とは、オペラッド結合にほかなりません。
カリー化コンビネータと評価コンビネータ
平面タングル達が作るオペラッドを PT とします。PTのオペレータ X のプロファイルは α1, ..., αk→β と書けます。ここで、α1, ..., αk は内円周で、β は外円周です。プロファイル α1, ..., αk→β を持つオペレータの集合を PT(α1, ..., αk→β) と書くことにし、これを、圏のホムセットに倣って、オペラッドのオペセット〈opeset〉と呼びましょう。
幾つかのオペセット(の直積)からオペセットへの写像をコンビネータ〈combinator〉と呼びます*6。ラムダ計算で重要なコンビネータに、カリー化コンビネータと評価コンビネータがあります。
カリー化コンビネータ〈Currying combinator〉は次の形です。
- Curry:PT(α1, ..., αk→β)→PT(α1, ..., αk-1→[αk→β])
矢印がイッパイ出てきてますが:
- α1, ..., αk→β の矢印は、オペレータ(平面タングル)のプロファイルの区切り。
- [αk→β] の矢印は、指数型を表す書き方の一部。
- まんなか辺の矢印は、写像を表す矢印。
カリー化は、内円周 αk のラベル(ここでは明示してない)に関してラムダ抽象することによって実行されます。
評価コンビネータ〈evaluation combinator〉は次の形です。
- Eval:PT(Γ→[α→β])×PT(Δ→α)→PT(Γ, Δ→β)
ここで、ΓとΔは、円周(型)を何個か並べたリストです。
評価は、ベータ変換、すなわちオペラッド結合によって実行されます。
平面タングル・オペラッドPT上のラムダ計算は、デカルト閉圏上のラムダ計算などに比べると、制約が多くぎごちない感じがします。一方で、原初的なラムダ計算の姿を見ることができる題材とも言えます。より洗練された計算デバイスに仕上げるには、(円板ではなく)方体を使い、ストリング図の値はコンパクト閉圏に取るようにするとよさそうです。が、今日はここまで。
*1:穴(内円周)のラベルは、「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」の言葉で言うなら、テンプレート変数名です。テンプレート変数には、プレースホルダー、シェマ変数、パターン変数、マクロ変数などの別名があります。
*2:足し算と掛け算からなる単純項は、1次以下の多項式になります。
*3:誤解を避けるために、チョーカー〈choker〉(短いネックレス)と呼ぼうかとも思ったのですが、言葉を増やすのをやめて、「円周」で間に合わせます。
*4:通常のラムダ計算で、空虚なラムダ抽象を許しているのは、それに対する意味論がハッキリしているからです。平面タングルの場合、空虚なラムダ抽象に意味付けできる保証がないので、とりあえずは禁止します。
*5:ラムダ・ラベルではないラベルと同じ名前にリネームすることはできません。同じ名前が二箇所に現れるのはダメ。