このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

ホップ代数の絵算 3：対蹠が反準同型射であること

雑記／備忘

「ホップ代数の絵算」シリーズの第3回（いちおう完結）です。

  1. ホップ代数の絵算 1：準備編
  2. ホップ代数の絵算 2：割り算と逆元

「ホップ代数の絵算 2」の最後に次のように書きました。

もう1回くらい続きます。次はたぶん ∇;S = X;(S×S);∇ を示します。

というわけで、今回 ∇;S = X;(S×S);∇ を示します。

内容：

  1. 状況の再確認
  2. 反準同型射
  3. 対蹠が反準同型射であるとは
  4. 割り算の定理を使って反準同型性を示す
  5. 一段落

状況の再確認

「ホップ代数の絵算 1」のコメント欄にて HNさんに色々とご指摘とご教示をいただいたので、それを踏まえて状況を整理しておきます。

前回の「ホップ代数の絵算 2：割り算と逆元」において、Δ;(f×f;S);∇ = !;i を示しました。f;S を 1/f と書いて、f*g := Δ;(f×g);∇、 1 := !;i という略記も採用すると、この事実は f*(1/f) = 1 と書けます。しかしホップ代数の一般論からは f*(1/f) = 1 が出ない（反例がある）ので、僕が想定している仮定が一般論よりは強いものになっているようです。

その「想定している仮定」とは、圏Cに前もってΔと!が備わっていることです*1。

  1. 圏Cは、対称モノイド圏であり、×, 1, σ をそれぞれ、モノイド積、モノイド単位、対称だとする。
  2. 圏Cの任意の対象Aに対して、ΔA:A→A×A, !A:A→1 による (A, ΔA, !A) が余モノイドになっている。
  3. 圏Cの任意の射は次の性質を持つ：
    1. Δ;(f×f) = f;Δ
    2. f;! = !

このような圏Cがあったとして、C内の群対象をCのホップ代数と呼びます。典型的な例は、集合圏Setに対して、ΔAをAからA×Aへの対角射として、!AはAから終対象 1 = {0} への唯一の射だと定義した圏における群対象です。これは、普通の群の定義になります。

ベースの圏を有限次元のベクトル空間の圏としても同様な構成はできますが、次の点で集合圏とは異なります。

  • 終対象とモノイド単位が一致しない（零空間と1次元空間）なので、！を一意的に定義はできない。
  • すべての線形写像が Δ;(f×f) = f;Δ、f;! = ! を満たすとは限らない。

よって、Δと！を定義した後で、射を制限した圏を作らないと「想定している仮定」を満たす圏にはなりません。

反準同型射

「・」が集合A上で定義されたなんらかの二項演算だとして、f:A→A に関して次の概念を定義できます。

f:A→B で、B上にも二項演算があれば、同様に準同型写像と反準同型写像を定義できます。

反準同型写像の概念を圏に対して一般化すれば、反準同型射（anti-homomorphism, antimorphism）を定義できます。反準同型射を定義するには「2つのモノの並び順をひっくり返す」操作が必要なので、圏は対称モノイド圏である必要があります。σを対称（symmetry, permutation）、∇を二項演算（に対応する射）とすると、次が反準同型射の定義です。

  • fが反準同型射である ⇔ ∇;f = σ;(f×f);∇

f:A→A だとして、域と余域をハッキリと書けば：

  • ∇A:A×A→A
  • f:A→A
  • σA,A:A×A→A×A
  • f×f:A×A→A×A

もっと一般に f:A→B だとすると：

  • fが反準同型射である ⇔ ∇A;f = σA,A;(f×f);∇B

対蹠が反準同型射であるとは

で、今回の目的の定理（定理2、T2）ですが、絵で描くと次のようです。

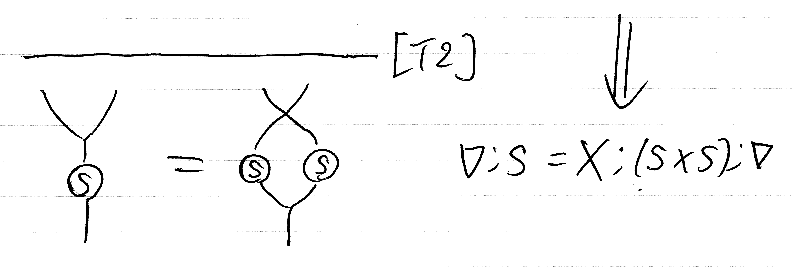
横棒の上は空っぽなので、特に仮定は必要とせずに、∇;S = X;(S×S);∇ が成立するってことです。Xはσと同じで対称のことです、Xのほうが形が絵に近いのでXも使います。Hをホップ代数（の台対象）として添字もちゃんと書くと：

  • ∇H;SH = XH,H;(SH×SH);∇H

ウヘーッ、やっぱり添字は鬱陶しいので適宜省略します。

さて、「fが反準同型射である ⇔ ∇;f = X;(f×f);∇」という定義と定理1を見比べると、「Sが反準同型射である ⇔ ∇;S = X;(S×S);∇」なので、定理1を言い換えると：

これは、(x・y)-1 = y-1・x-1、あるいは記号を変えて 1/(x・y) = (1/y)・(1/x) に対応する事実です。この点を以下に説明しましょう。

f:A→H、g:A→H だとして、fとgのペア <f, g> を、<f, g> := ΔA;(f×g) として定義します。<f, g>;∇ は、見慣れた記法では f・g と書けます。<f, g>;∇;S なら 1/(f・g) です、なぜなら：

  • <f, g>;∇;S = (<f, g>;∇);S = (f・g);S = 1/(f・g) （記法の約束から）

定理2から、∇;S = X;(S×S);∇ ですから

  • <f, g>;∇;S = <f, g>;X;(S×S);∇

ここで、<f, g>;X = <g, f> を使えば、

  • <f, g>;∇;S = <g, f>;(S×S);∇ = <g;S, f;S>;∇ = <1/g, 1/f>;∇

<1/g, 1/f>;∇ は (1/g)・(1/f) と書けるので：

  • 1/(f・g) = (1/g)・(1/f)

割り算の定理を使って反準同型性を示す

「ホップ代数の絵算 2：割り算と逆元」で示した定理1＝割り算の定理は次のものでした。

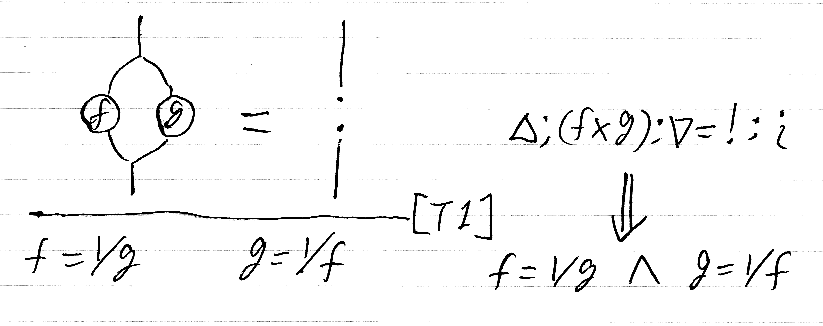
もっと簡略な記法を使えば、f*g = 1 ⇒ (f = 1/g かつ g = 1/f) です。大ざっぱに言えば、fとgが互いに逆数であることを示すには、掛けて1になることを見れば十分であると主張してます。

定理2は、「∇;S = X;(S×S);∇」ですが、左辺の X;(S×S);∇ をTと置くと、次の形です。

  • ∇;S = T

∇;S は 1/∇ なので、定理2の主張は：

  • 1/∇ = T （Tは∇の逆数）

定理1によれば、これを示すには、∇*T = 1 （∇とTを掛けて1）が言えれば十分です。∇*T = 1 を詳しく書くと：

  • ΔH×H;(∇H×T);∇H = !H×H;∇1;iH

絵に描くと次のようになります。白丸は対蹠Sです。

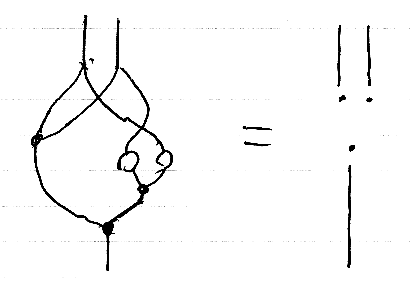
この形になってしまえばしめたもの、絵算の本領発揮です。この等式は下のような計算（絵の変形操作）で示せます。

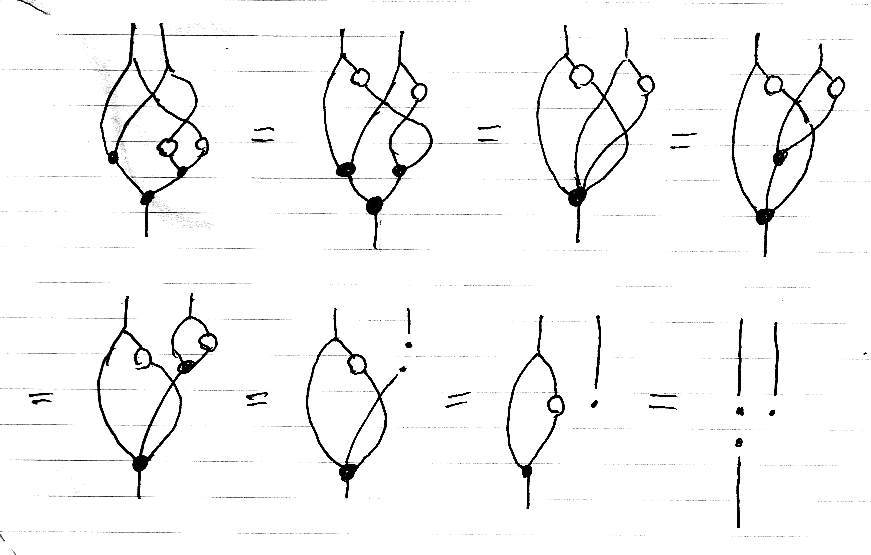
一段落

「ホップ代数の絵算」シリーズはこれで一段落とします。圏論的なセッティングで、仮定を強くして、絵算を使って、ホップ代数の入り口だけ紹介しました。ホップ代数を計算（computation）の定式化に使うなら、表現論や物理とは少し違う使い方になると思うのですが、あんまりよく分かりません。とりあえず雰囲気だけはつかめたので、機会があれば使ってみたいですね。

*1:[追記]明示的に書いてないのですが、余乗法（対角）Δは余可換であることも通常仮定します。 Δが余可換とは、Δ;σ = Δ のことです。[/追記]

*2:[追記]ここでは割り算の定理を使いますが、対蹠が反準同型であることは割り算の定理とは独立です。割り算の定理を使わない直接的な証明があるので、ホップ代数の一般としても「対蹠は反準同型射」が成立します。[/追記]