正規表現は文字列とのマッチングのためのパターンであり、マッチする文字列の集合を定義します。文字列ではなくてツリーに対しても「パターン」を考えてみます。ツリーのパターンも、それとマッチするツリーの集合を定義します。
ツリーパターンの概要
ツリーは有向グラフの一種で、ノードと辺からなります。ノードは小さい黒丸、辺は単なる実線(特に矢印は付けません)で描くことにします。ルートが上、リーフ(葉)は下に描きます。ノードや辺に対して名前や値を付けることはしません。したがって、同じ形状のツリーは同じとみなします。以下にツリーの例をいくつか挙げます*1。
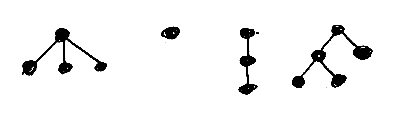
正規表現に'*'や'|'のようなメタ文字があるのと同じように、ツリーパターンもメタノード/メタ辺を含みます。それは次の3つです(後で説明します); 何もないことを表すノード、選択肢を表すノード、逆行する辺です。
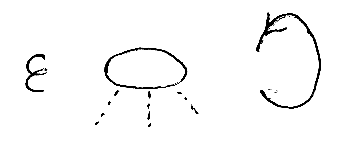
次はツリーパターンの一例です。この例が定義する集合を後で具体的に調べます。
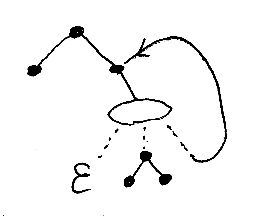
εノードと選択肢ノード
黒い小さな丸と実線はツリーのインスタンスを構成するノードと辺を表します。ツリーパターンでは、それとは別な特殊なノード/辺が現れます。
まず、ノードも辺もない空なツリーをε(イプシロン)で表します。εを含むツリーは、そのεノード自体とεノードに向かう辺を取り除いたツリーと同じです。以下の絵を見ればわかるでしょう。
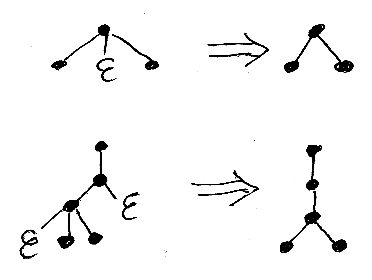
選択肢を表すノードは大きめの白丸で表します。選択肢ノードの下にぶら下がるどれかのサブツリーを選んで使っていいものとします。選んだ選択肢ごとに別なツリー(またはツリーパターン)が生まれます。以下の例で、⇒ の右側が選択肢を選んだ結果を並べたものです。
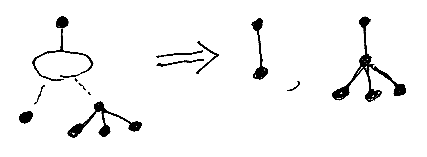
εノードと選択肢ノードを組み合わせると、サブツリーの省略可能性を表現できます。次の例を見れば明らかでしょう。⇒ の右側では、εノードは取り除いてあります。
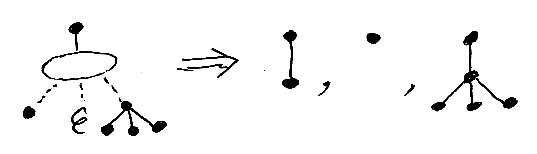
逆行する辺とサイクル
繰り返しパターン(再帰的パターン)を表現するには、ツリーの末端から上の方(ルート側)に戻る辺を使います。以下は戻る(逆行する)辺を含む簡単な例です。
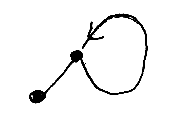
逆行する辺があると、ツリー内にサイクル(循環)ができます。「サイクルを持たないグラフ」をツリーと定義しているので、「サイクルを持つツリー」という言葉は変なんですが、まー、固いことは言わないことにします。で、サイクルを持つグラフをどう解釈するかというと、サイクルをどんどん展開(unfold, unwind)して無限ツリーとみなします。
サイクルの無限展開は、慣れないと意外と難しいので手順を詳しく説明します。まず、サイクルに名前を付けます;例えばAとしましょう。次にサイクルをちょん切って、切り離した両端に名前をコピーします。上側の名前は外側の大きなツリーを表す名前、下側の名前はプレースホルダーの名前と解釈します。ここまでが準備です。
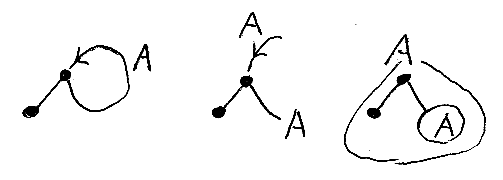
準備が終わったら、名前が付いたツリーをコピーして、片一方のプレースホルダーAに、ツリー全体としてのAを“代入”します。内側のAをもう一度逆行する辺で繋ぎ合わせると、サイクルが一段階だけ展開されているのがわかります。
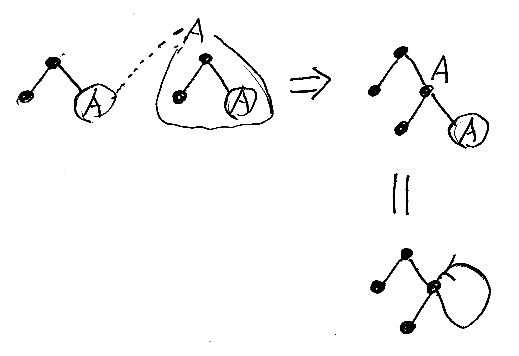
慣れてしまえばイチイチこんな手順を踏まなくても展開できます。無限に展開すると、サイクルはなくなって無限ツリーができます。
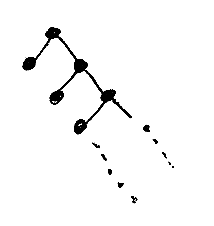
パターンから作られるツリーの集合
冒頭の例に挙げたツリーパターンが、どのような集合を定義するか見てみます。まず、サイクルを展開して無限ツリーを作っておきます。選択肢ノードも無限回登場しますが、図では上から順に番号を振ってあります。
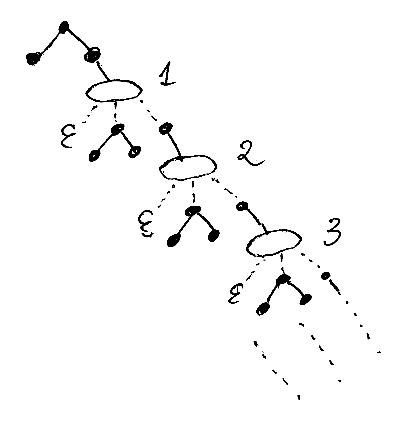
実際のツリー(インスタンスツリー)は有限ツリーです。それぞれの選択肢ノードでどれかの選択肢を選ぶと有限ツリーができます。しかし、選択肢は無限にあるので、どこでどんな選択をするかによって無限個のインスタンスツリーが生まれます。それら全てのインスタンスツリーを寄せ集めた集合が、ツリーパターンにより定義される集合となります。
選択肢ノード1, 2, 3 における選択から得られる6つのツリーだけを図示します。選択肢ノードは無限にあるので、実際には無限個のツリーが生まれます。
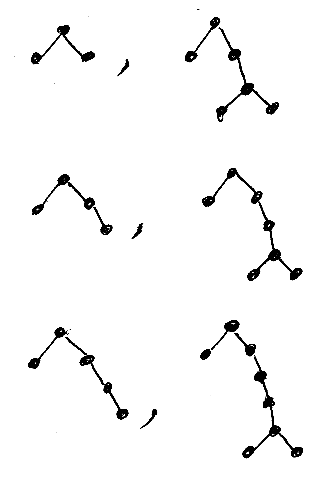
このようにして得られたツリーの無限集合は(ツリーの)正規集合の例です。文字列の正規集合(正規言語)とよく似た性質を持ちます。と、今日は一例を紹介したところでオシマイ。
*1:http://d.hatena.ne.jp/m-hiyama/20100422/1271902182 では、「ここがルート」という目印を描いていましたが、今回は目印がありません。どれがルートかは見れば分かると思うので。