実務上の必要性から生じた話なんですが、「問題としてちょっと面白いかもな」と思ったので紹介します。特別なアイディアやトリッキーな方法は不要なのでクイズという感じじゃないですね。普通に「プログラミングの練習問題」でしょう。算術計算だけで出来るので、プログラミング言語や実行環境は問いません。
n次元単体
0次元単体とは1個の点、1次元単体とは線分、2次元単体とは内部を含む三角形、3次元単体とは内部を含む四面体です。もっと次元が高いn次元単体(simplex)は類推してください。
単体は三角形の一般化なので、n次元単体をΔnと書くことが多いですが、σnとかsnとかを使うこともあります。ここでは、単体の特別な(そして標準的な)実現を、σn、snで表すことにします。
n次元のユークリッド数空間をRnとします*1。σnはRn+1の部分集合、snはRnの部分集合として次のように定義します。
- σn = {(x1, ..., xn, xn+1)∈Rn+1 | x1 ≧ 0, ..., xn ≧ 0, xn+1 ≧ 0, x1 + ... + xn + xn+1 = 1}
- sn = {(x1, ..., xn)∈Rn | x1 ≧ 0, ..., xn ≧ 0, x1 + ... + xn ≦ 1}
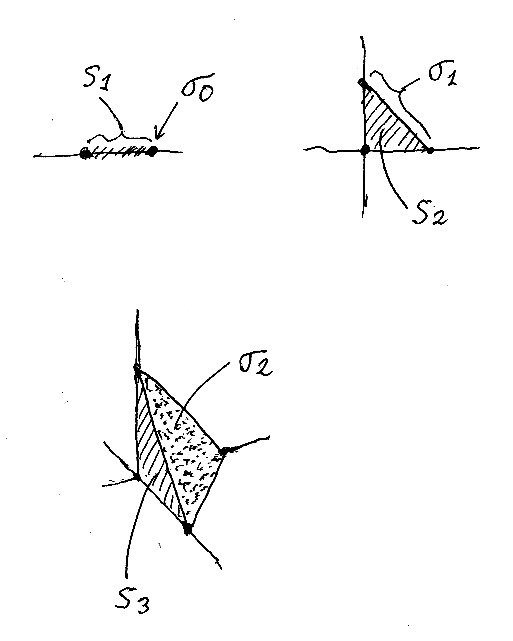
σ0, σ1, σ2, s1, s2, s3 を絵に描くと次のようです。
格子点
σnとsnに非負数値のパラメータkを導入して次のように定義します。
- σn(k) = {(x1, ..., xn, xn+1)∈Rn+1 | x1 ≧ 0, ..., xn ≧ 0, xn+1 ≧ 0, x1 + ... + xn + xn+1 = k}
- sn(k) = {(x1, ..., xn)∈Rn | x1 ≧ 0, ..., xn ≧ 0, x1 + ... + xn ≦ k}
ここで、連続な空間Rnの代わりに、座標が整数である空間Znを考えます。座標が整数である点は格子点と呼びます。以下、σn、snの定義も格子点に限定します(でも、同じ記号を使い続けます)。パラメータkも非負整数に限定します。
四面体=三角錐をスライスする状況を考えると、次のことがわかります。
- sn+1(k) = σn(0) + σn(1) + ... + σn(k)
ここでプラス記号「+]は集合の合併なのですが、集合の直和になっているので「∪」より「+」のほうが感じが出ます。
第一象限の格子点の列挙
(n+1)次元の格子点空間Zn+1で、すべての座標が非負であるような格子点の全体は“第一象限”を形成します。第一象限は、次のような無限直和で書けます。
- σn(0) + σn(1) + σn(2) + ...
これは、sn+1(k)のkを無限に飛ばした形をしているので、記号的には「第一象限 = sn+1(∞)」と書いてもいいでしょう。
さて問題は、N = {0, 1, 2, 3, ...} として、N→sn+1(∞) という双射(全単射)写像を作ってください、というものです。n = 0 のとき、N→s1(∞) は自明です。
この双射写像は、sn+1(∞) = σn(0) + σn(1) + σn(2) + ... というスライス構造を尊重するようにしてください。つまり、最初にσn(0)を列挙し、次にσn(1)を列挙し、それからσn(2)を列挙し、という具合です。
σn(k)に含まれる格子点の個数をN(n, k)として、{0, 1, ..., N(n, k)}→σn(k) という双射を先に考えるといいかもしれません。最終的には、すべてのnに対する fn:N→sn+1(∞) が欲しいのですが、fn達をひとつの2変数関数f(n, i)と考えると、f:N×N→Σn=0..∞[sn+1(∞)] となります。
大きなシグマは集合の無限総和のつもりですが、Σn=0..∞[sn+1(∞)]とは、非負整数を成分とする長さ任意のリスト達の集合のことです。