圏論的宇宙と反転原理と次元付きの記法

「ファンタジー： (-1)次元の圏と論理」の最後の一文：

このファンタジーに、リアリティが加わるといいんですけど…

圏論的宇宙をチャンと理解するのはなかなかに難しいですが、記法を整備するくらいはできるので、やっておきましょう。

内容：

圏論的宇宙と反転原理

公理的集合論の宇宙〈universe〉は非常に単純化されていて、この世に存在するすべてのモノは集合と考えます。要素という概念はありますが、ふたつの集合の関係性において、片方が果たす役割を要素と呼んでいるだけです。

アトム〈atom | 原子〉を導入すると、アトムは要素にしかなれないので絶対的要素である、と言ってもいいでしょう。銀河〈galaxy〉を導入すると（銀河については「現場の集合論としての有界素朴集合論」を参照）、銀河は要素になり得ないので絶対的集合だと言えます。

アトム／銀河を導入しても、集合論的宇宙は比較的シンプルです*1。では、圏論的宇宙はどうでしょう。高次圏も含めたn-圏達の全体が圏論的宇宙なんですが、そもそも、n-圏の生態が分かってない*2ので、宇宙の構造もハッキリしません。ごくラフな（詩的な）描像は、昨日「ファンタジー： (-1)次元の圏と論理」で述べました。

昨日の記事で反転原理（または反転仮説）というものを提案したのですが、これは、単一のn-圏の構造は、圏論的宇宙の構造を反転させた姿をしているようだ、という経験則です。

「反転」の意味を説明しましょう； 圏論的宇宙は、(-2)-圏の階層、(-1)-圏の階層、0-圏の階層、1-圏の階層、… のように、圏の次元により階層化されています。一方で単一のn-圏は、0-射の階層、1-射の階層、2-射の階層、… のように射の次元により階層化されています。この2つの階層のあいだに次のような関係があります。

宇宙の階層	n-圏Kの階層
(-2)-Cat	Homn+2K
(-1)-Cat	Homn+1K(α, β)
0-Cat	HomnK(f, g)
…	…
(n-1)-Cat	Hom1K(A, B)

なんかゴチャゴチャしているので、次元（整数値）だけを取り出すと：

宇宙の階層	n-圏Kの階層
-2	n+2
-1	n+1
0	n
…	…
n-1	1

「…」の部分を一般的に書けば：

• j ←→ n - j （-2 ≦ j ＜ n）

次元のあいだの関係は単純で、たしかに反転しています。ゴチャゴチャしている部分を以下で説明し、同時にゴチャゴチャを整理する記法を導入します。

プロファイル記法

圏論のなかでは、f:A→B という記法がまず間違いなく使われます。見たことあるでしょ。この書き方の A→B の部分をfのプロファイル〈profile〉と呼びます。プロファイルとホム集合〈homset | ホムセット〉は次のように関係しています。

• f:A→B in C ⇔ f∈C(A, B)

このとき、AとBはCの対象ですが、A（あるいはB）がCの対象であることを A in C と書きます。A:C と書く人もいますが、この書き方は採用しません。その理由は後で述べます。

• A in C ⇔ A∈|C|

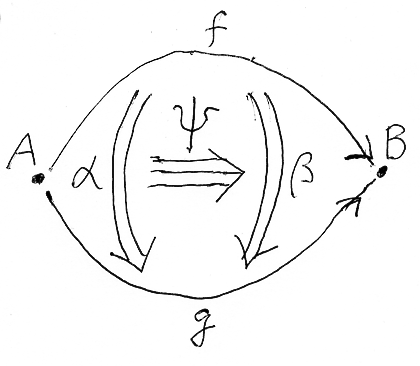
次に高次圏を考えます。いきなり一般のn-圏は難しいので、Kは2-圏だとします。Kの対象はA, Bなど、射はf, gなど、2-射はα, βなどで表します。対象と射については普通の圏（1-圏）と同じ書き方をします。

• A in K ⇔ A∈|K|
• f:A→B in K ⇔ f∈K(A, B) ん、これでいいのか？

2-圏において、K(A, B)は単なる集合ではなくて圏でした。ホム圏と呼ぶのでした（昨日の記事参照）。fは、ホム圏K(A, B)の対象なので、

• f:A→B in K ⇔ f∈|K(A, B)|

となります。

αがfからgへの2-射のとき、2-射らしくコロンを2つ、二重の矢印を使います。

• α::f⇒g

fとgは共通の域・余域を持っていて、f, g:A→B です。この事情まで書くと：

• α::f⇒g:A→B in K

ホム圏との関係は次のよう。

• α::f⇒g:A→B in K ⇔ ( α∈Mor(K(A, B)), dom(α) = f, cod(α) = g, (f, g∈|K(A, B)|), A, B∈|K| )

同値の右辺の記述が煩雑なので、これは後で整理することにします。

もし、Kが3-圏ならば、3-射もあるので、それを次のように書きます。

• Ψ:::α≡>β::f⇒g:A→B in K

もうお分かりですね。3個のコロン、三重の矢印です。

一般に、n-射のプロファイルはn個のコロン、n重の矢印です。n個のコロンを :ⁿ 、n重の矢印を →ⁿ と書くことにすれば、n-射σのプロファイルは、

• σ :ⁿ x →ⁿ y

n = 0 のときは0-射＝対象のプロファイル、0個のコロンなので、:⁰ なんですが、これは空になってしまうので、:⁰ の代理にキーワード'in'を使うことにしています。先の3-射のプロファイルを累乗（上付きの指数）形式で書き直せば：

• Ψ :³ α →³ β :² f →² g :¹ A →¹ B :⁰ K

見やすくはないのですが、nがどんな大きな数でも、コロンと矢印の系列としてn-射のプロファイルを書けます。

n-射の形状

ここでちょっとした注意事項をはさみます。

現状、n-圏の定義は色々あって、異なる定義が同値なのか否か？ どれが適切なのか？ そもそも適切性の基準があるのか？ などが分かっていません。n-圏を構成するn-射として、どういう“形状”を選ぶかで、異なる流儀になります。n-射の形状としては次があります（もっと他もあるかも知れません）。

1. 球体〈globe〉
2. 単体〈simplex〉
3. 方体〈cube〉
4. マルチトープ〈multitope〉
5. オペトープ〈opetope〉
6. デンドレックス〈dendrex〉
7. テータ・セル〈theta cell〉

このなかで、最も簡単そうに思えるのが球体です。証明支援系Globularの名称は、球体の"globe"から来ています。実際、Globularは球体モデルを採用した高次圏ソフトウェアです。

前節で紹介したn-射のプロファイルの書き方は、n-射の形状がn-球体であることを前提にしています。球体以外の形状を採用するアプローチだと、プロファイルはもっと複雑になります。

僕は、一番扱いやすいという理由で球体アプローチを支持しています。他の形状を否定はしませんが、難しいので、とりあえずは球体アプローチでやってみよう、という態度です（けっこう安易）。

n-圏への球体アプローチの雰囲気は次の記事で書いています。

• おとぎ話としてのn-圏 -- 計算できる図形達の世界
• バタニンの球複体 とりあえず導入

ホムシングとモーシング

圏の定義も幾つかの流儀がありますが、たぶん一番よく使われている定義は、圏Cの対象〈object〉の集合（または類）Obj(C)と、圏Cの射〈morphism〉の集合（または類）Mor(C)から出発するものでしょう。

Mor(C)から始めた場合、Cのホム集合〈homset | ホムセット〉は次のように定義します。

• Hom_C(A, B) := {f∈Mor(C) | dom(f) = A, cod(f) = B}

Obj(C)は|C|と略記され、Hom_C(A, B)はC(A, B)と略記されます。

以下、集合と類（集合より大きいかも知れない集まり）を区別せずに単に集合と言います。Obj(C)をObj_C、Mor(C)をMor_Cと下付き添字で書くことにします。Mor_Cを、圏Cのモー集合〈morset | モーセット〉と呼ぶことにします。「モー」はmorphismの"mor"です。

n-圏に対して、そのホム集合、モー集合を定義したいのですが、また2-圏の例から始めます。Kを2-圏とします。まずは、0-ホム集合と0-モー集合を対象集合として定義します。この定義がベースとなります。

• Hom⁰_K = Mor⁰_K := |K|

より高次のホム／モーを定義していきますが、それらは必ずしも集合ではないので、ホムシング〈homthing〉、モーシング〈morthing〉と言い換えることにします。実は、モーシングはほとんどの場合集合で、(n + 2)次元のときだけモー値となります。

モーシングより先にホムシングを考えます。反転原理により、2-圏Kの1-ホムシングは1-圏です。よって、1-圏（普通の圏）の対象集合をとれます。その対象集合が1-モーシングです。

• Mor¹_K(A, B) := |Hom¹_K(A, B)|

このモーシングは、2つの対象A, Bでパラメータ付けられた集合の族です。モー集合達を全部寄せ集めてパラメータなしのモーシング（モー集合）を定義します。

• Mor¹_K := ∪{A, B∈Mor⁰_K | Mor¹_K(A, B)}

この定義の右辺は、集合族の総合併を意味します。

2次元のホムシングは2-射の集合（つまりホム集合）です。

• Hom²_K(f, g)

fとgの両端が同じ（共端）でないと、2-射は存在しないので、f, gの共通するプロファイルを添えておけば：

• Hom²_K(f, g:A→B)

モーシングはホムシングの対象部分をとります。

• Mor²_K(f, g) := |Hom²_K(f, g)|

2-ホムシングHom²_K(f, g)は単なる集合でした。集合Sに関してその対象部分|S|はその集合自身（|S| = S）なので、次のように書いても同じです。

• Mor²_K(f, g) := Hom²_K(f, g)

パラメータ付きのモーシング（モー集合）達を全部寄せ集めてパラメータなしの2-モーシングを作るので、

• Mor²_K := ∪{f, g∈Mor¹_K | Mor²_K(f, g)}

ここまでは普通の構成です。3次元（(2 + 1)次元）と4次元（(2 + 2)次元）のホムシング／モーシングの構成には、負次元の圏に対する反転原理を使います。圏論的宇宙のビッグバン以前の状況（昨日の記事参照）が、3次元と4次元のホムシング／モーシングに反映します。

2-圏Kの3次元のホムシングは真偽値（つまりホム値）です。

• Hom³_K(α, β) （これはTrueかFalseのどちらか）

αとβに共通するプロファイルを添えておけば：

• Hom³_K(α, β::f⇒g:A→B)

モーシングはホムシングの対象部分…、いやっ、真偽値にはもはや対象部分という概念がないので、値そものをとります。

• Mor³_K(α, β) := Hom³_K(α, β)

パラメータなしの3-モーシングは、真偽値True, Falseの寄せ集めでブール集合になります。

• Mor³_K := ∪{α, β∈Mor²_K | Mor³_K(α, β)} = {True, False}

次元4は、圏論的宇宙が始まる前の状態を反映するので、真も偽もなく、個体と全体の区別さえない状況で考えます*3。

• Hom⁴_K = Mor⁴_K = *

'*'は何もないことを示す目印です。集合論的宇宙でも圏論的宇宙でも、「はじめに無ありき」から出発するのは面白いですね。

任意のnに対する記法と略記

前節では、Kを2-圏として話をしました。2を任意のnとしても、同様にホムシング／モーシングを構成できます。0-ホムシング、0-モーシング、対象集合は同じものだとして、整数jを 1 ≦ j ≦ n とします。j次元のモーシングは次のように定義されます。

• Mor^j_K(x, y) := |Hom^j_K(x, y)|
• Mor^j_K := ∪{x, y∈Mor^j-1_K | Mor^j_K(x, y)}

j = n + 1, j = n + 2 に関しては、いつでも同じで、

• Morⁿ⁺¹ = {True, False}
• Morⁿ⁺² = *

です。

jを大きい方から順に n + 2, n + 1, n, ..., 1 と見ていくと、圏論的宇宙の歴史を再現します。j = 0、つまり対象集合は特殊で、n-圏Kのなかに(n - 1)-圏がどのくらい含まれるかをコントロールするインデックスの領域のようです*4。

通常の圏論において、対象集合とホム集合に略記がありました。

• |C| := Obj(C)
• C(A, B) := Hom_C(A, B)

高次圏でも同様な略記を導入しましょう。

• |K|^j := Mor^j_K （0 ≦ j ≦ n + 2）
• K^j(x, y) := Hom^j_K(x, y) （x, y∈Mor^j-1_K、1 ≦ j ≦ n + 1）

これらの略記を使えば、n-圏の階層的構造をかなりスッキリと表現できます。

*1:構造がシンプルというだけであって、やさしいわけではありません！

*2:有限のnだけでなく、∞-圏もあります。∞-圏はもっと分かりません。

*3:開闢以前の世界は混沌であり虚無であったわけです。なんか仏教ぽい香りがしますね。

*4:対象集合の特殊性を何かうまく解釈できないかと考えているんですけど、今のところよく分かりません。