準マルコフ圏達を対象類とする厳密2-圏と、そのなかの余モナドについて幾つかの記事を書きました。
何を言いたいのかと言うと:
- 準マルコフ余モナドの余クライスリ圏は再び準マルコフ圏になるだろう。
ザッとあたりを付けてみたところ、(細部の見落としはあるかも知れませんが)たぶんこれは成立します。
あたりを付けるときに使った計算法は絵算〈{graphical | diagrammatic | pictorial} {calculus | computation}〉です。この計算過程を記述するのが大変、効率的な記述方法・伝達方法が事実上ないんですよね*1。
例えば、解説記事「圏論の随伴をちゃんと抑えよう: お絵描き完全解説」では、手描きの絵をスキャンした画像を入れてますが、長い計算になると手描きと画像化は辛い。
XyJaxで頑張って描くというのも試したことがあります(「カリー/ハワード対応のための記法・図法」参照)。これは再利用が可能ですが、一枚描くのが大変。
絵でなくて、テキストを2次元的に配置する方法をやってみたことがあります。
さかんに「疲れる」と言ってますが、実際疲れます。それでも、現状では2次元レイアウトのテキストくらいで妥協するしかない気がするので、この方法を再度試してみます。
内容:
- 最初の記事(シリーズ目次あり): 準マルコフ圏からなる2-圏
- 次の記事: 反ラックス・モノイド関手の一般余結合律
- 前の記事: 準マルコフ余モナド
記述の基本
モノイド圏または2-圏の1-射/2-射を行列形式でテキスト記述します。
射 は縦方向に次のように書きます。
は次のようです。
一般に、上から下に向かって「対象 射 対象 射 ‥‥」と代わりばんこに並びます。最後は対象です。このような配置を として、さらに横に併置(区切り記号に縦棒)と縦に併置をします。
横に併置はモノイド積または横結合を表し、縦に併置は縦結合を表します。
ルールはこれだけです。
「絵算の威力をお見せしよう」で出した次の絵図を考えてみます。
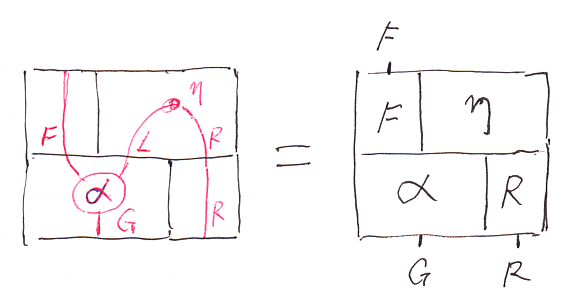
次のように行列形式で書けます。 は横結合の図式順演算記号です。
線形代数におけるニョロニョロ関係式(「カッコイイけど使える線形代数とは?」参照)は次のように書けます。
モノイド圏の構造同型射 をちゃんと考慮すれば次のようになります。
ウーム。ニョロニョロな感じがしない(苦笑)。
事例
色々と不満や問題点はありますが、幾つかの等式を、前節の方法で書き下してみます。
反ラックス・モノイド関手の余乗法の自然性
としましょう。
が自然であることは次のように書けます。
これは、なんとかストライプ図をイメージできるかな。
反ラックス・モノイド関手の余乗法の余結合律
余結合律(に類似の法則)は次のようです。
もとのストライプ図を知っていれば思い出すキッカケにはなるでしょう。
反ラックス・モノイド関手の余乗法と対称との強調
が特定の対象
を左から掛ける関手のときは、この等式は次のストリング図で描けます(「準マルコフ圏の掛け算関手」参照)。
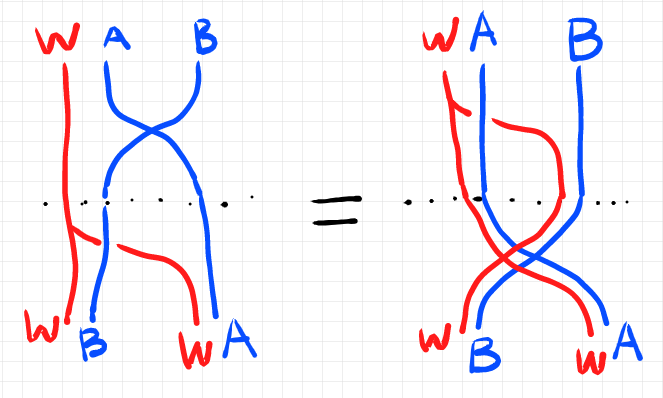
比較的素直なストライプ図なら、ギリ再現できる感じですね。
*1:homotopy.io(globularの後継)、quantomatic、CATEGRAPHER、DisCoPy などの証明支援系は描画機能を備えてますが、描画用には効率的でもお手軽でもありません。