確率的推論・判断の計算法：マルコフ・テンソル絵算

比較的最近書いた記事「同時確率分布の圏の使用例：超具体的」、「アブダクションと確率的推論」などで触れたように、確率（真である度合）を使った推論や判断が面白な―、と思っています。

でも、確率的推論・判断のための計算ってけっこう難しいです。系統的な計算手順も必要だし、何をどう計算するかの指針を与える手法も欲しいです。ここでは、行列／テンソル計算（計算手順）とストリング図（指針策定）を使った方法を紹介します。内容的には“マルコフ・テンソルの圏”を扱うのですが、厳密な定義や根拠／背景は省略して、具体的な例題を中心に述べます。

随分と長い記事です。この記事全体のまとめや言い残したことなどを最後に書いているので、「おわりに」から先に読むのもいいかも知れません。

内容：

状況設定と問題

インフルエンザのようなウィルス感染症を考えます。ただし架空の病気で、これから述べる設定はフィクションです。設定に出てくる数値は、必要なときは繰り返し引用するので覚える必要はありません。全体の状況をザッと把握してください。

このウィルスに感染してもしばらくは発病せず、発病前に治療薬（抗ウィルス剤）を飲めば発病を抑えることができます*1。また、現在感染しているかどうかの検査も行えます。

感染検査は完璧ではありません。感染していても陰性と出ることもあれば、逆に感染してないのに陽性反応が出ることもあります。検査（test）の精度は次のテーブルで表現できます。

test
	感染してる	感染してない
陽性	98%	5% (誤認)
陰性	2% (誤認)	95%

治療薬もまた完璧ではありません。治療薬の効果（effect）は次のとおりです。（次のテーブルは二項述語テーブルですが、その定義は次節で。）

effect
(二項述語)	感染してる	感染してない
投与する	発病10%	発病0%
投与しない	発病80%	発病0%

感染していて薬を投与しなくても、2割の人は発病せず、何の問題もありません。

もしウィルスに感染して発病すると、苦しい思いをするし、仕事を休むなど様々なダメージを受けます。その損害を金銭に換算して10万円としましょう。検査には300円、治療薬には1000円かかるとします。

この状況で、我々の行動には次のような選択肢があるでしょう。

1. 何もしない。
2. 検査を受けずにとりあえず薬を飲む。
3. 検査を受けて、もし陽性が出たら薬を飲む。

他にも行動の可能性があるでしょうが、この3つを主に考えます。検査代／治療薬代というコストと感染発病したときの損害（金銭換算）を合わせて損失（loss）と呼ぶことにして、上記3種の行動に対する損失を比較しましょう。もちろん、不確定な要素があるので、損失は確率的に評価することになります。これは、確率を考慮した平均損失を計算する問題です。

どんな道具を使うのか：マルコフ行列

確率的計算を系統的に行う上で最も重要な概念はマルコフ行列です*2。なので、マルコフ行列と、マルコフ行列のなかで特殊な形のものを紹介します。

成分が非負実数値で、各列（縦方向）の合計値が1である行列をマルコフ行列（Markov matrix）と呼びます。次の2つはマルコフ行列の例です。

1番目の行列は、「同時確率分布の圏の使用例：超具体的」で出した製造機械の不良率、2番目は今回の感染検査の精度を表す行列testです。“素の”行列では現実的意味が分からないので、この記事では見出し付きのテーブルを使って書きますが、テーブルも実質的には行列（マトリクス）です。

マルコフ行列は、条件付き確率の表現です。例えば、感染検査〈testテーブル〉の第1列（左列）に注目すると：

	感染してる
陽性	98%
陰性	2% (誤認)

これは、「感染している」という条件のもとでの陽性／陰性の出現確率を表します。第2列（左列）も同様に、「感染してない」と条件を付けての陽性／陰性の確率ですね。

マルコフ行列の特殊なものとして次の形を考えます。

• 1列だけのマルコフ行列
• 2行だけのマルコフ行列

1列だけのマルコフ行列は確率分布（probability distribution）と呼びます。混乱の恐れがないのなら、単に分布（distribution）とも呼びます。ここでは、形状が1列であることを強調して分布列（distribution column）とも呼びます。次は分布列の例です（次節に出てきます）。

infection
	*
感染してる	1%
感染してない	99%

星印（'*'）はダミーの見出しです。「最初の行は見出し行」という形に揃えるためですが、後で出てくる図示（ストリング図）とも揃えるためです。

2行だけのマルコフ行列で、行の2つの見出しが true/false, Yes/No の意味を持つとき、そのマルコフ行列をファジー述語（fuzzy predicate）と呼びます。混乱の恐れがないのなら、単に述語（predicate）とも呼びます。例えば、検査精度の表はファジー述語です。述語であることを明白にするために、見出しのパターンを「××, 非××」とします。例えば：

test
	感染	非感染
陽性	98%	5% (誤認)
非陽性	2% (誤認)	95%

先ほどの分布列〈infection列〉も2行なので述語になっています。

infection
	*
感染	1%
非感染	99%

ファジー述語もマルコフ行列なので、列の和は1です。なので、第1行だけ書けば第2行は計算（1 - x）で出ます。述語を1行だけで書くときは次のように書きます。左上の欄に註釈で「(述語)」と書いて、実際には2行であることを警告します。

test
(述語)	感染	非感染
陽性	98%	5% (誤認)

述語かつ分布列なら1個だけの欄で書けます。

infection
(述語)	*
感染	1%

治療薬の効果を表すテーブルは、そのままではマルコフ行列ではありませんが、次のような形で書けばファジー述語、すなわち2行のマルコフ行列です。

effect
	感染, 投与	感染, 非投与	非感染, 投与	非感染, 非投与
発病	10%	80%	0%	0%
非発病	90%	20%	100%	100%

これをさらに1行形式で書くと：

effect
(述語)	感染, 投与	感染, 非投与	非感染, 投与	非感染, 非投与
発病	10%	80%	0%	0%

横方向の4つの見出しを縦横2×2に分解した形が最初に出した〈effectテーブル〉の形です。縦横の組み合わせを引数とする述語なので、これは二項述語（binary predicate）と呼びます。「二項」の代わりに「二変数」「ニ引数」と言っても同じです。

effect
(二項述語)	感染	非感染
投与	発病10%	発病0%
非投与	発病80%	発病0%

もし、1つの欄のなかに発病と非発病を詰め込むなら：

effect
	感染	非感染
投与	発病10%, 非発病90%	発病0%, 非発病100%
非投与	発病80%, 非発病20%	発病0%, 非発病100%

このテーブルをチャンと(?)書きたいなら、3次元のテーブル（キューブ）にすべきなんです。{発病, 非発病}を第3の方向に取って、8個の欄を作るのです。でも、3Dで描くのは容易じゃないので2Dテーブルでやりくりします。

他に、同時確率テーブルや関数行／2変数関数テーブルなども後で使いますが、必要になったときに説明します。

何もしないときの平均損失

まず、何もしないときを考えます。検査代／薬代のコストはかからないので、感染して発病したときの損害10万円だけを考えます。

ファイナンスの確率に関して『量子ファイナンス工学入門』の前田先生は：

明日の株価予想が当たる確率は50%、外れる確率も50%である。当たるか、当たらないか分からない、つまり外れる確率が50%もある賭けに大事なお金を使うことについては慎重な判断を下すべきであろう。

せきしろさんによる確率の計算例では：

かわいい子が来る確率は来るか来ないかだから50%、その子がつまずく[檜山注：隣の席に座ろうとして転ぶ]確率は同様に50%、そして恋が生まれる確率も、生まれるか生まれないかで50%、よって1/8となり、12.5%となる。

このでんでいくと、発病する確率は50%、発病しない確率も50%で、平均損失は 10万円×1/2 + 0円×1/2 = 5万円 となります。これだと二人に一人は10万円損失している、つまり発病していることになります。全人口の半分が発病している状況ならこの計算は正しいですが、それが事実かどうか分かりません*3。

実は、感染率の値がないと平均損失の計算はできません。そこで、全人口に対する感染者の比率は1%とします。100人に1人が感染しています。感染者の発病率は80%だったので、0.8%が発病の確率です。

この状況は、1000本に8本の当たりがあるクジを引くのと同じです。当たると賞金10万円なら、平均賞金額（賞金の期待値）は 10万円×8/1000 + 0円×992/1000 = 800円 です。今のケースでは賞金が損失となり、平均損失額が800円です。各個人としては、損失ゼロか10万円のどちらかですが、集団全体として損失を均等に負担するなら一人あたり800円になります。

行列計算で考える

前節の「何もしないとき」の例では、数値（スカラー）の計算だけで平均損失が出ました。前々節で述べたマルコフ行列なんて要りません … いやっ、背後には行列計算があるのです。

感染（infection）の比率は次の1列のマルコフ行列、つまり分布列でした。

infection
	*
感染	1%
非感染	99%

発病（development）の比率は2行のマルコフ行列、つまり述語です。

develop
	感染	非感染
発病	80%	0%
非発病	20%	100%

なお、この行列developは、薬の効果effectの非投与の部分を取り出したものです。逆に言うと、effectは、developに“薬を投与した場合の情報”を追加したものです。

感染／非感染を集約した発病率の計算は、2つのマルコフ行列の掛け算を計算します。

ウィルスにA型ウィルスとB型ウィルスがあるならば、もっと行列計算らしくなります。

infection2
	*
A感染	0.5%
B感染	0.5%
非感染	99%

B型ウィルスは発病率が低いとしましょう。

develop2
	A感染	B感染	非感染
発病	80%	60%	0%
非発病	20%	40%	100%

感染ウィルスの種類と非感染の別を集約した発病率は、3行1列マルコフ行列（右側）infection2と2行3列マルコフ行列（左側）develop2の掛け算で計算します。

より一般に、確率分布を表す1列マルコフ行列（上の具体例ではinfection2）と条件付き確率を表すマルコフ行列（上の具体例ではdevelop2）の掛け算により、条件の場合分けを集約した確率分布を計算できます。

さて、平均損失の計算には、次の損失関数（loss function）が登場します。

loss
(関数)	発病	非発病
損失額	10万円	0円

関数のテーブルは1行だけの行列（マルコフ行列ではない！）とみなして、発病率分布のマルコフ行列（先に計算済の分布列 (develop infection)）と掛け算します。これが前節で行った計算で、結果は800円です。

これも、非発病の損失額が0円なので、あんまり行列計算の感じがしません。ちょっとだけ複雑なケースとして、検査を受けて何もしなかったときを考えてみましょう。損失関数は次のようになります。

loss2
(関数)	発病	非発病
損失額	10万300円	300円

A型ウィルスとB型ウィルスがある場合での平均損失計算は、次の行列計算となります。

この程度なら、直感とスカラー計算だけでも何とかなりますが、事情が複雑になれば行列計算が有利になります。行列による定式化は次のようにします。

1. 確率分布は、1列だけのマルコフ行列（分布列）で表現する。
2. 条件付き確率は、マルコフ行列で表現する。
3. 損失関数は、1行だけの行列で表現する。これはマルコフ行列ではない。
4. 平均損失は、損失関数の1行と分布列の1列を掛けたスカラーとなる。

薬を飲むときの平均損失

検査を受けずにとりあえず薬を飲む場合を考えましょう。最初に損失関数を提示しておきます。

loss3
(関数)	発病	非発病
損失額	10万1000円	1000円

1000円は薬代です。

この損失関数を発病率の分布列で平均すれば求める結果が得られます。よって、発病率の分布列を求めればいいことになります。「何もしないとき」とは違い、薬の効果があるので、仮に感染していても発病リスクは低くなり、全体として発病率は低下します。

〈effectテーブル〉から薬を投与（administrate）時の情報だけを取り出します。それをeffect_admとしましょう。

effectadm
	感染	非感染
発病	10%	0%
非発病	90%	100%

これと、集団全体での感染率の情報infectionを使います。

infection
	*
感染	1%
非感染	99%

これらから、薬投与時の発病率は 1%×10% + 99%×0% = 0.1%、よって平均損失は 10万1000円×0.1% + 1000円×99% = 1100円 です。何もしないときの800円より損失は増加してますが、1000円は薬代のコストなので、発病時のダメージの平均は100円に減っています。この計算の背後には、次のような行列計算があると言えます。

ところで、「何もしないとき」の計算で出てきたdevelopは、effecから薬を非投与（not administrate, no administration）時の情報だけを取り出したものなので、develop = effect_noadm と書けます。effect_noadmと書き換えて先の計算を再掲すると：

「何もしないとき」と「薬を飲むとき」で類似の計算をしていることが分かります。そうであれば、「何もしないとき」と「薬をのむとき」を混ぜたような計算も同様にできそうです。次節でやってみます。

2変数損失関数の平均

前々節では「何もしないとき」、前節では「薬を飲むとき」の計算をしました。今度は、薬を投与（administration）する／しないが確率的な場合を考えます。

admin
	*
投与	25%
非投与	75%

この投与率の解釈は、集団内で薬を投与する人と投与しない人がいて、その比率が25:75である状況です。あるいは別な解釈として、私個人の投与／非投与を、コインを2回投げて2回とも裏が出たら投与する、と決めるような状況です。

いずれにしても、発病を抑える薬の投与率が25%の前提で平均損失を求めてみます。薬代は損失に含めますが、感染検査はないとします。

損失に薬代を入れると、損失関数は2変数になります。{投与, 非投与}×{発病, 非発病} のそれぞれで損失額は違います。

loss3
(2変数関数)	投与	非投与
発病	損失10万1000円	損失10万円
非発病	損失1000円	損失0円

この損失関数の平均を計算するには、{投与, 非投与}×{発病, 非発病}上で定義された確率分布が必要です。平均（期待値、積分）というのは確率分布（より正確には確率測度）を使って計算されるものだからです。

今回のケースでは、薬を使う／使わないの判断は各人に任されています。検査を受けて決めるわけではないので、「感染しているかどうか」と「薬を投与するかどうか」は独立と仮定します。もし、ウィルスの潜伏期間中でも多少の症状が出る場合、この独立性はあやしくなります。「なんか調子悪いな、例のウィルスかな？ とりあえず薬飲んどこう」と考える人がいれば、「感染しているかどうか」が「薬を投与するかどうか」の判断に影響します。でも今は独立だとします。

感染率を表すinfectionと投与率を表すadminから、{感染, 非感染}×{投与, 非投与} 上の同時確率分布を求めるには、独立性の仮定から掛け算（確率の積の法則）が使えます。ちょっと無理矢理ですが、行列の掛け算の形で計算します（後述のテンソル積を使うのが自然です）。結果をinfAdmとします。

結果をテーブルで示すならば：

infAdm
(同時分布)	感染	非感染
投与	0.25%	24.75%
非投与	0.75%	74.25%

一列の分布列の形式にするなら：

infAdm
	*
感染, 投与	0.25%
感染, 非投与	0.75%
非感染, 投与	24.75%
非感染, 非投与	74.25%

{感染, 非感染}×{投与, 非投与} 上の確率分布であるinfAdmと、{感染, 非感染}×{投与, 非投与} の各場合ごとに発病率を与える条件付き確率であるeffec（薬の効果）から、{感染, 非感染}×{投与, 非投与}×{発病, 非発病} 上の同時確率分布を計算できます。

（無理矢理な）行列計算を使う手順だけ述べると、2行4列行列の形に書いたeffectにinfAdmから作った4行4列の対角行列（大文字始まりのInfAdmとする）を右から掛けます。その結果はinfAdmDev（infection, administration, developmentの同時確率分布）とします。

見出し付きのテーブルの形にすれば：

infAdmDev
(同時分布)	感染, 投与	感染, 非投与	非感染, 投与	非感染, 非投与
発病	0.25%	6%	0%	0%
非発病	2.25%	1.5%	24.75%	74.25%

感染／非感染の情報は不要なので、足し算して集約すると：

admDev
(同時分布)	投与	非投与
発病	0.25%	6%
非発病	27%	75.25%

これで、損失関数loss3と形が揃いました。

loss3
(2変数関数)	投与	非投与
発病	損失10万1000円	損失10万円
非発病	損失1000円	損失0円

損失関数loss3を横1行、同時分布admDevを縦1列にして掛け算すれば平均損失を計算できます。

どんな道具を使うのか：行列の一般化

今まで出てきた二項述語や同時分布は、2次元テーブルの形をしていますが、マルコフ行列ではありませんでした。そのため、不自然な行列の変形や計算を強いられます。任意個数の添字（インデックス）を持った非負実数の族としてテンソルを定義し（次節で）、そのなかでマルコフ・テンソルを特定しましょう。

行列を成分表示するとき、a_{j i} のような2個の添字（二重インデックス）を使います。テンソル計算では、添字を上下にして a^j_i と書くのが普通です。ここでは、添字（インデックス）をブラケットに入れることにします； a[j, i] ですね。

a[j, i] という書き方ではまだ問題があるのでさらに工夫します。iが列番号でjが行番号のとき a[j←i]と矢印で区切ります。iとjを逆順に書きたいときは a[i→j] とします。矢印を使うと、行列の掛け算を「右から左」でも「左から右」でも自由に書けます。

• (ba)[k←i] = Σ(j| b[k←j]a[j←i] ) … 右から左の順の積、併置
• (a;b)[i→k] = Σ(j| a[i→j]b[j→k] ) … 左から右の順の積、セミコロン

添字のi, jなどは整数値でなくても、任意の有限集合の要素でいいとします。すると、X, Yを有限集合として (a[y←x] | x∈X, y∈Y)、または (a[x→y] | x∈X, y∈Y) のような形で行列を書けます。例えば、感染検査の精度を表す行列は、test = (test[r←i] | i∈{感染, 非感染}, r∈{陽性, 非陽性}) で、各成分は次のとおりです。

• test[陽性←感染] = 98%
• test[非陽性←感染] = 2%
• test[陽性←非感染] = 5%
• test[非陽性←非感染] = 95%

集団全体の感染率の分布列は infection = (infection[i←t] | t∈{*}, i∈{感染, 非感染}) で：

• infection[感染←*] = 1%
• infection[非感染←*] = 99%

一般に、a = (a[y←x] | x∈X, y∈Y) （あるいは、a = (a[x→y] | x∈X, y∈Y)）のとき、行列aのプロファイルは X→Y （XからY）だといい、そのことを a:X→Y と書きます。感染検査の精度test、集団全体の感染率infectionならば：

• test:{感染, 非感染}→{陽性, 非陽性}
• infectiont:{*}→{感染, 非感染}

これらの行列の積 (test infection) = (infection;test) のプロファイルは {*}→{陽性, 非陽性} となります。これでお気付きの方もいるでしょうが、行列の全体も、マルコフ行列の全体も圏となります。が、その詳細はここでは割愛します。

{感染, 非感染}のように、{A, 非A}の形の集合が頻繁に出てくるので、A? = {A, 非A} としましょう。例えば：

• 感染? = {感染, 非感染}
• 陽性? = {陽性, 非陽性}

疑問符'?'は、"or not"と読むといいでしょう。また、{*}も頻繁に出てくるので 1 = {*} と置きます。この略記を使ってtestとinfectionのプロファイルを書けば：

• test:感染?→陽性?
• infectiont:1→感染?

どんな道具を使うのか：マルコフ・テンソル

薬の効果を表す情報effectは、2次元のテーブルではうまく表せないものでした。ひとつの欄に複数の値を記入することになります。

effect
	感染	非感染
投与	発病10%, 非発病90%	発病0%, 非発病100%
非投与	発病80%, 非発病20%	発病0%, 非発病100%

または、縦横の見出しを組み合わせて横の見出しに潰します。

effect
	感染, 投与	感染, 非投与	非感染, 投与	非感染, 非投与
発病	10%	80%	0%	0%
非発病	90%	20%	100%	100%

どちらにしても不自然。実は、〈effectテーブル〉の成分は3つの添字（インデックス）を持つのです。effect = (effect[i, a, d] | i∈感染?, a∈投与?, d∈発病?)。アレ、区切りは矢印でした、矢印はどう入れましょうか？ 薬の効果の計算では、{感染, 非感染}×{投与, 非投与}の要素を与えて、{発病, 非発病}上の分布を知りたいので、関数的に考えれば 感染?×投与?→発病? というプロファイルになります。

つまり、薬の効果を表す情報は effect = (effect[i, a→d] | i∈感染?, a∈投与?, d∈発病?) となります。3つの添字のうちiとaが入力側、dが出力側です。矢印を逆向きにしたいなら effect = (effect[d←i, a] | i∈感染?, a∈投与?, d∈発病?) でもかまいません。

一般に、いくつかの添字（インデックス）を持つ実数（ここでは非負実数）の族で、添字が入力側と出力側に分割されているものをテンソル（tensor）と呼びます*4。行列は添字を2つ持つテンソルです。薬の効果を表すeffectは添字を3つ持つテンソルの例です。

テンソルの入力側添字を固定します； 例えば effect[感染, 非投与→d]。出力側の添字を動かして総和を取りましょう； Σ(d∈発病? | effect[感染, 非投与→d])。この例では総和が1になります。どの入力側添字（の組）に対しても出力側の総和が1のとき、そのテンソルをマルコフ・テンソル（Markov tensor）と呼びます。マルコフ行列は特別な形のマルコフ・テンソルです。

同時確率分布もマルコフ・テンソルとみなせます。次の例を考えてみます。

admDev
(同時分布)	投与	非投与
発病	0.025%	0.6%
非発病	24.975%	74.4%

これはマルコフ行列ではないので、（方便として）1列に直してマルコフ行列と考えました。

admDev
	*
投与, 発病	0.025%
投与, 非発病	24.975%
非投与, 発病	0.6%
非投与, 非発病	74.4%

行の見出しは 投与?×発病? の要素です。一方、ただ1つの列の見出しはダミーの'*'です。列見出しの集合が入力側、行見出しの集合が出力側なので、同時確率分布admDevのプロファイルは 1→投与?×発病? と考えられます。出力側の 投与?×発病? 上で総和を取ると1になるので、同時分布admDevはマルコフ・テンソルです。

念のために、マルコフ・テンソルの定義を一般的に述べれば： f = (f[x₁, ..., x_n→y₁, ..., y_m] | x₁∈X₁, ..., x_n∈X_n, y₁∈Y₁, ..., y_m∈Y_m) という添字族がマルコフ・テンソルだとは、次の条件をみたすことです。

• 任意の a₁∈X₁, ..., a_n∈X_n に対して、Σ(y₁∈Y₁, ..., y_m∈Y_m | f[a₁, ..., a_n→y₁, ..., y_m]) = 1

例に挙げたeffectとadmDevは：

• 薬の効果effectは、プロファイルが 感染?×投与?→発病? であるマルコフ・テンソルである。
• 薬の効果と感染分布／投与分布から作った同時確率分布admDevは、プロファイルが 1→投与?×発病? であるマルコフ・テンソルである。

複雑なプロファイルを持つマルコフ・テンソルを考えることができますが、今回必要なのは2項ファジー述語に対応するマルコフ・テンソルと、同時確率分布に対応するマルコフ・テンソルです。また、マルコフ・テンソルに関する様々な操作がありますが、系統的説明は省略して、必要なときに必要なだけ導入することにします。

検査を受けて判断するときの平均損失：準備

まず、損失関数を書いておきます。

loss4
(2変数関数)	投与	非投与
発病	損失10万1300円	損失10万300円
非発病	損失1300円	損失300円

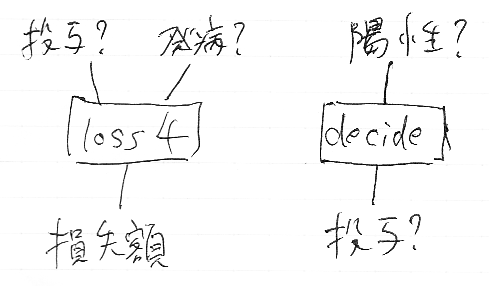
300円は検査の費用です。loss4はマルコフ・テンソルではなくて関数です。関数としてのプロファイルを書いておくと： loss4:投与?×発病?→損失額 (as 関数) です。

loss4の平均値を求めるには、1→投与?×発病? というプロファイルを持つ同時確率分布admDev2が必要です。この同時分布admDev2を求めることが課題です。

同時分布admDev2を求めるには、今まで出てきたtest, effect, infectionを使います。これらをまとめておくと：

名前	意味	プロファイル
test	感染検査の精度	感染?→陽性?
effect	治療薬の効果	投与?×感染?→発病?
infection	集団全体の感染率	1→感染?

これらのマルコフ・テンソルを下のような図で表します。マルコフ・テンソルはオダンゴで描きます。オダンゴから出たワイヤーに添字集合をラベルします。上が入力側の添字集合、下が出力側の添字集合です。入力ラベル集合が 1 = {*} のときは、ワイヤーを描かずに'*'マークを付けることにします。

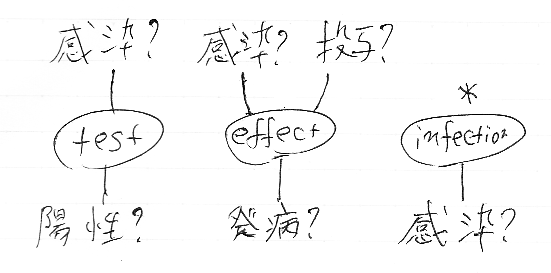
関数は四角い箱で表しましょう。損失関数 loss4:投与?×発病?→損失額 が2変数の関数です。検査の結果を見て薬の投与／非投与を決める判断関数（decision function）も関数 decide:陽性?→投与? (as 関数) です。

念のため注意しておくと、有限集合から有限集合への関数（写像）は、マルコフ行列として表現できます。decide:陽性?→投与? をテーブルで表すなら：

decide
	陽性	非陽性
投与	100%	0%
非投与	0%	100%

テーブルの欄の値が100%か0%であるマルコフ行列は関数（写像）を表すのです。有限集合のあいだの関数（写像）は特殊なマルコフ行列なのだとも言えます。損失関数 loss4:投与?×発病?→損失額 は、値の領域（損失額の集合、Rと同型とする）が有限集合ではないのでマルコフ“行列”にはなりませんが、マルコフ核（マルコフ行列／マルコフ・テンソルの一般化）にはなります。

さて、求めるべき同時分布 admDev2:1→投与?×発病? を図示すると次の形です。

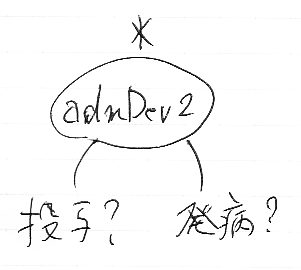
admDev2の実際の構成は次々節以降で行います。次節では、マルコフ行列に対する操作の説明をします。

マルコフ・テンソルの種類と操作

X₁, ..., X_n, Y₁, ..., Y_m が(n + m)個の有限集合だとして、f:X₁, ..., X_n→Y₁, ..., Y_m というプロファイルのテンソルを反変n階／共変m階のテンソルと呼びます。あるいは、nを反変の階数、mを共変の階数、(n + m)を階数と呼びます。この言い方は歴史的なもので、あんまり分かりやすくないのですが、他の言い方も見当たらないので致し方なく使うことにします。

今までに出てきたマルコフ・テンソルの種類を階数と共に挙げておきます。

名称	プロファイル	階数
一般的マルコフ行列	X→Y	反変1階／共変1階
確率分布（1列のマルコフ行列）	1→X	反変0階／共変1階
ファジー述語（2行のマルコフ行列）	X→A?	反変1階／共変1階
二項述語	X×Y→A?	反変2階／共変1階
同時確率分布	1→X×Y	反変0階／共変2階
有限集合のあいだの写像	X→Y	反変1階／共変1階

マルコフ・テンソルが、これらのどれか一つだけに分類される、ということではありません。例えば、infection:1→感染? は確率分布でもありファジー述語でもあります。

今回の計算で使うマルコフ・テンソルの操作には次のものがあります。

1. 2つのマルコフ・テンソルの結合（composition）
2. 2つの確率分布のテンソル積（tensor product）
3. 確率分布とマルコフ・テンソルからの同時化（同時確率分布の作成；jointification）
4. 同時確率分布の周辺化（周辺分布の作成； marginalization）

これらの操作を一般的に述べるのではなく、今回使う範囲に限って述べます。説明の後に絵があります。

結合（composition）

マルコフ行列（反変1階／共変1階のマルコフ・テンソル）に限れば、結合は既に出てきています。f = (f[x→y] | x∈X, y∈Y), g = (g[y→z] | y∈Y, z∈Z) に対して、fとgの結合f;gは次のように定義されます。

• (f;g)[x→z] = Σ(y∈Y | f[x→y]g[y→z])

f;gのプロファイルは X→Z となります。

x, y, zが (x₁, ..., x_n), (y₁, ..., y_m), (z₁, ..., z_k) のようになっても同じで、f:X₁×...×X_n→Y₁×...×Y_m と g:Y₁×...×Y_m→Z₁×...×Z_k の結合を定義できます。

テンソル積（tensor product）

確率分布 p = (p[x] | x∈X) と q = (q[y] | y∈Y) があるとき、これらのテンソル積pqは次のように定義されます。なお、p[x]はp[*→x]の略記です。

• (pq)[x, y] = p[x]q[y]

pqのプロファイルは 1→X×Y となります。

テンソル積は、感染率 infection:1→感染? と投与率 admin:1→投与? から infAdm = infectionadmin を作る際に使っています。単なる計算としてテンソル積を作ることはいつでもできますが、背後にある確率変数の独立性がないと誤った計算になることがあります。

同時化（jointification）

確率分布 p = (p[x] | x∈X) と、マルコフ行列 f = (f[x→y] | x∈X, y∈Y) があるとき、同時分布 ^p∩f を次のように定義します。

• (^p∩f)[x, y] = p[x]f[x→y]

これが、マルコフ行列fの分布pによる同時化で、条件付き確率を同時確率に変換する操作です。^p∩f のプロファイルは 1→X×Y となります。

周辺化（marginalization）

同時分布 f = (f[x, y] | x∈X, y∈Y) に対して、X方向への周辺化 f↓^X,Y_X と、Y方向への周辺化 f↓^X,Y_Y は次のように定義されます。

• (f↓^X,Y_X)[x] = Σ(y∈Y | f[x, y] )
• (f↓^X,Y_Y)[y] = Σ(x∈X | f[x, y] )

f↓^X,Y_X, f↓^X,Y_Y のプロファイルはそれぞれ 1→X, 1→Y です。

上付き添字X, Yは省略して、f↓_X, f↓_Y でもいいでしょう。また、X×Y×Z上の同時分布をY×Zに周辺化する操作なども同様に定義できます。不要な情報を集約するときに周辺化を使います。

---

結合、テンソル積、同時化、周辺化を図示すると次のようになります。

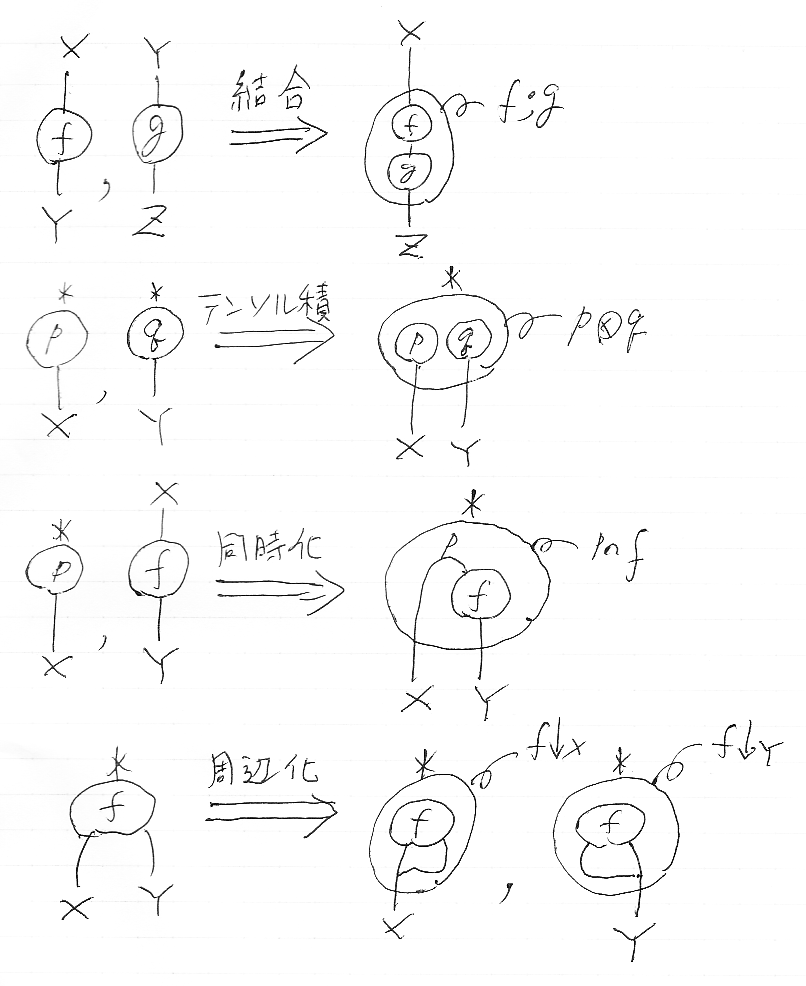
検査を受けて判断するときの平均損失：計算

admDev2:1→投与?×発病? を次の4ステップで計算します。

1. [test;decideの計算] 感染検査の精度を表す test:感染?→陽性? と、検査の結果から投与／非投与を決める関数 decide:陽性?→投与? の結合 test;decide:感染?→投与? を求める。
2. [infAdm2の計算] test;decide:感染?→投与? を、感染率 infection:1→感染? により同時化して、^infection∩(test;decide) = infAdm2 : 1→感染?×投与? を求める。
3. [infAdmDev2の計算] 薬の効果 effect:感染?×投与?→発病? を、infAdm2:1→感染?×投与? により同時化して、^infAdm2∩effect = infAdmDev2 : 1→感染?×投与?×発病? を求める。
4. [admDev2の計算] 同時確率分布 infAdmDev2:1→感染?×投与?×発病? を周辺化して、確率分布 admDev2:1→投与?×発病? を求める。

test;decide:感染?→投与?

testとdecideの結合は、マルコフ行列の掛け算として自然に計算できます。

test;decide
	感染	非感染
投与	98%	5%
非投与	2%	95%

decideの行列は単位行列になっていますが、陽性? の空間から 投与? の空間に変換しているので無意味ではありません。decideを他の写像に切り替えると、別な結果が得られます。例えば、検査の結果によらず薬を投与するという判断もあります。

infAdm2:1→感染?×投与?

infAdm2 = ^infection∩(test;decide) は、本来テンソル計算で定義されますが、無理に行列計算でやるなら、分布列（1列のマルコフ行列）infectionを対角行列化して右からtest;decideに掛けます。infectionの対角行列化をInfectionとします。

infAdm2
(同時分布)	感染	非感染
投与	0.98%	4.95%
非投与	0.02%	94.05%

感染検査の不完全さから、感染しているにも関わらず非投与の人が0.02%、感染してないのに投与してしまう人が4.95%います。

infAdmDev2:1→感染?×投与?×発病?

infAdmDev2 = ^infAdm2∩effect も、テンソル計算で定義されます。これも無理に行列計算でやるなら、effectを2行4列の行列の形にして、infAdm2の4成分を対角行列化した4行4列行列InfAdm2を右からeffectに掛けます。

infAdmDev2
(同時分布)	感染, 投与	感染, 非投与	非感染, 投与	非感染, 非投与
発病	0.098%	0.016%	0%	0%
非発病	0.882%	0.004%	4.95%	94.05%

admDev2:1→投与?×発病?

感染に関する情報は不要なので、列を足し算して集約します。

admDev2
(同時分布)	投与	非投与
発病	0.098%	0.016%
非発病	5.832%	94.054%

---

目的としたadmDev2が求まったので、損失関数loss4（下に再掲）をadmDev2で重み付けした平均を求めます。

loss4
(2変数関数)	投与	非投与
発病	損失10万1300円	損失10万300円
非発病	損失1300円	損失300円

10万1300円×0.098% + 1300円×5.832% + 10万300円×0.016% + 300円×94.054% = 473.3円 となります。検査を受けて適切な判断と予防治療をすれば、平均損失額はだいぶ下がります。

おわりに

この記事を書くにはちょっと苦労しました。最初は、圏論的定式化と実例の両方を一緒に書こうと思ったのですが、量が増えすぎるのであきらめました。ウィルス感染症に関わる検査、治療薬、損失などを計算する事例だけにしました。例題の計算に必要な概念は説明していますが、系統的でも網羅的でもありません。僕はストリング図に沿って計算してますが、それを再現するのも疲れるので、図の提示も断片的です。

しかしそれでも、確率的問題の定式化と計算に、テンソルとその図式表現であるストリング図が有効であることが多少は伝わったでしょう。

テンソルの数値的計算は、行列計算を流用しています。この方法はバッドノウハウで、あまり好ましくありません。テンソルの数値計算ができるソフトウェアを探せば良かったのかも知れませんが、数値計算は手元にあったR言語処理系で行いました（Rにもテンソル計算パッケージはあるようです）。

マルコフ・テンソルは、確率分布、条件付き確率、同時確率に一様な定式化を与える点で便利なのですが、これらの意味的な違いを意識したほうがいいときもあります。この事の背景には、確率分布（確率空間）、条件付き確率、同時確率のそれぞれに対応する圏 Prob、CondProb、JointProb の存在があります。これらの圏達とその相互関係はまたの機会に述べるつもりです。

確率分布／条件付き確率／同時確率を計算する行為は、ある種の推論だと言えます。確率的推論を行うための論理系（logical system）をうまく定義できれば、それは日常生活の論理を（古典論理より）うまく説明できるかも知れません。「アブダクションと確率的推論」で断片的に述べたことを、もう少し体系化できる可能性があります。

現時点での感触としては、「計算と論理と圏の三者が密接に関連している」というカリー／ハワード／ランベック対応（Curry-Howard-Lambek correspondence）の確率版があるような気がします。

オマケ：マルコフ・テンソルと関数の一覧

矢印が'→!'と書いてあるのは関数です。

1. test: 感染? → 陽性?
2. effect: 感染?×投与? → 発病?
3. infection: 1 → 感染?
4. develop: 感染? → 発病?
5. infection2: 1 → AB感染?
6. develop2: AB感染? → 発病?
7. loss: 発病? →! 損失額
8. loss2: 発病? →! 損失額
9. loss3: 発病? →! 損失額
10. infAdm: 1 → 感染?×投与?
11. admin: 1 → 投与?
12. infAdmDev : 1 → 感染?×投与?×発病?
13. admDev: 1 → 投与?×発病?
14. loss4: 投与?×発病? →! 損失額
15. admDev2: 1 → 投与?×発病?
16. decide: 陽性? →! 投与?
17. infAdm2: 1 → 感染?×投与?
18. infAdmDev2: 1 → 感染?×投与?×発病?
19. admDev2: → 投与?×発病?

*1:この設定のモトは、T-ウィルスと抗ウィルス剤。レイン・オカンポは薬を打ったが手遅れでした。カルロスは感染してましたが、アンジー（アンジェラ・アシュフォード）が持っていた抗ウィルス剤で発病を免れました。

*2:より一般的な概念はマルコフ核ですが、離散有限の場合ならマルコフ行列で間に合います。

*3:ベイズ推論で、ほんとに何も分からないとき、暫定的に五分五分だと仮定することはあります。

*4:「テンソル」は多義語なので、多くの意味を持ちます。ここでは添字族をテンソルと呼ぶ、ということです。