ストリング図とテンソル計算：クソバカ丁寧編 - 檜山正幸のキマイラ飼育記 (はてなBlog)

$\newcommand{\Iff}{\Leftrightarrow} \newcommand{\id}{\mathrm{id}} \newcommand{\I}{\mathrm{I}} \newcommand{\X}{\mathrm{X}} \require{color} \newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }% \newcommand{\For}{\Keyword{For } }% \newcommand{\Define}{\Keyword{Define } }% \newcommand{\Where}{\Keyword{Where } }% \newcommand{\Holds}{\Keyword{Holds } }% \newcommand{\Declare}{\Keyword{Declare } }% \newcommand{\Therefore}{\Keyword{Therefore } }%$ ストリング図とテンソル計算に関して僕が言えること、言いたいことは「やってみてください」です。ある意味“機械的な作業”なので、やれば出来ます。ボブ・クック教授に言わせれば「幼稚園児でも出来る」（「幼稚園児のための量子力学とその周辺」参照）。もっとも、この記事では、字を知らない園児ではとうてい出来そうにない作業も扱いますが。

内容：

例題：行列の転置
特別なテンソル、象形文字と成分表示
ワイヤーベンディング・オペレーター
転置行列の構成
成分表示と計算

関連する記事：

続きの記事：

例題：行列の転置

行列のインデックスが無限集合になると厄介なので、インデックスの集合 $A, B$ は有限集合だとします。例えば、 $A = \{1, 2\}, B = \{1, 2, 3\}$ とかだと思ってかまいません。

行列としてのプロファイルが $f:A \to B$ である実数係数行列 $f$ を考えます。成分表示は：

$\quad f = (f(y \mid x))_{x\in A, y\in B}$

関数〈写像〉としてのプロファイルは $f:A\times B \to {\bf R}$ なので、ラムダ式で次のように書いても同じです。

$\quad f = \lambda\, (x, y)\in A\times B.(\, f(x, y)\;\in {\bf R}\,)$

$f$ への引数〈インデックス〉渡しの書き方が色々ありますが、全部同じ意味です。

$f(x, y)$
$f(y \mid x)$
$f_{y\, x}$
$f_x^y$
$f[x, y]$

「インデックスが $i, j$ じゃないと気持ち悪い」とかはショーモナイ感情なので、そんなところには拘らない！

さて、行列 $f$ の転置を $f^\dagger$ と書きます。すると：

$\quad f^\dagger :B \to A \:\text{ as matrix}\\ \quad f^\dagger :B\times A \to {\bf R} \:\text{ as function}\\ \quad f^\dagger = \lambda\, (y, x)\in B\times A.(\, f^\dagger(y, x)\;\in {\bf R}\,) \\ \qquad = \lambda\, (y, x)\in B\times A.(\, f(x, y)\;\in {\bf R}\,)$

行列の転置をストリング図で表すと次のようになります。

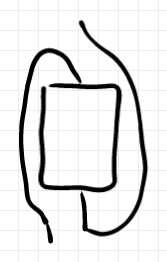
ちょっと形が卍に似てます（そんなに似てねーか）。この図がほんとに行列の転置になっていることを確認することが例題です。

特別なテンソル、象形文字と成分表示

行列を結合〈掛け算〉しても行列ですが、テンソル積すると行列の範囲に収まらないのでテンソル〈多行列 | polymatrix〉を考えます。テンソル $t$ のプロファイルは一般に、

$\quad t:(A_1, \cdots, A_n) \to (B_1, \cdots, B_m)$

ここで、 $A_1, \cdots, A_n, B_1, \cdots, B_m$ はすべて有限集合とします。このテンソルの関数〈写像〉としてのプロファイルは：

$\quad t: (A_1\times \cdots \times A_n) \times (B_1\times \cdots\times B_m) \to {\bf R}$

テンソルをストリング図に描くときは、テンソルの結合の方向を上から下、テンソルのテンソル積の方向を左から右にとります。これは僕の個人的な好みの描画方向で、人により描画方向の選択は色々です（「絵算（ストリング図）における池袋駅問題の真相」参照）。

描画方向「↓→」に関して、次の象形文字が使えます。

象形文字	キーワード	名称
$\I$	$\id$	恒等
$\X$	$\mathrm{swap}$	対称、入れ替え、スワップ、交差
$\Delta$	$\mathrm{copy}$	対角、コピー、分岐
$!$	$\mathrm{del}$	破棄、デリート、削除
$\cap$ または $\wedge$	$\mathrm{coev}$	余評価、単位
$\cup$ または $\vee$	$\mathrm{ev}$	評価、余単位

余評価〈単位〉と評価〈余単位〉は、描いたときの形状からベント〈bent（名詞）| 曲がり〉とも呼ばれます。ここでは、 $\cap,\cup$ は集合の共通部分／合併ではなくて、テンソルの名前〈固有名詞〉として使う象形文字です。

ボブ・クック教授が「幼稚園児でも出来る」と言っているのは、ストリング図をストリング図のまま変形する絵算〈{graphical | diagrammatic | pictorial} {calculus | computation}〉のことであって、テキストに書き下すとなると幼稚園児には無理です。園児は字が書けませんからね。

我々は大人なのでテキストに書き下すことにします。「絵で見れば簡単なことが、なんでこんなウジャウジャになってしまうんだ!?」と腹立たしいかも知れませんが、そこは大人なのだから我慢しましょう。大雑把な絵に対してテキスト記法は精密な情報を持っています。精密さと引き換えの煩雑さなのです。

最初は恒等。

$\Declare \I_{(A_1, \cdots, A_n)}: (A_1, \cdots, A_n) \to (A_1, \cdots, A_n) \:\text{ as tensor}\\ \Declare \I_{(A_1, \cdots, A_n)} : (A_1\times \cdots\times A_n) \times (A_1\times \cdots\times A_n) \to {\bf R} \:\text{ as function}\\ \For (x_1, \cdots, x_n) \in A_1\times \cdots\times A_n\\ \For (x'_1, \cdots, x'_n) \in A_1\times \cdots\times A_n\\ \Define \I_{(A_1, \cdots, A_n)}( x'_1, \cdots, x'_n\mid x_1, \cdots, x_n ) := \delta( (x'_1, \cdots, x'_n), (x_1, \cdots, x_n) )$

$\delta$ はクロネッカーのデルタなので：

$\Where \delta( (x'_1, \cdots, x'_n), (x_1, \cdots, x_n) ) := \\ \quad (\text{if }(x'_1, \cdots, x'_n) = (x_1, \cdots, x_n) \text{ then }1 \text{ else } 0)$

タプルが等しいことは成分ごとに等しいことなので：

$\quad (x'_1, \cdots, x'_n) = (x_1, \cdots, x_n) \Iff x'_1 = x_1 \land \cdots \land x'_n = x_n\\ \Therefore\\ \quad \delta( (x'_1, \cdots, x'_n), (x_1, \cdots, x_n) ) = \delta(x'_1, x_1) \cdots \delta(x'_n, x_n)$

次に余評価〈単位〉を書き下します。

$\Declare \cap_{(A_1, \cdots, A_n)}: () \to (A_1, \cdots, A_n, A_1, \cdots, A_n) \:\text{ as tensor}\\ \Declare \cap_{(A_1, \cdots, A_n)}: \{*\} \times (A_1\times \cdots\times A_n\times A_1\times \cdots\times A_n) \to {\bf R} \:\text{ as function}\\ \For (x_1, \cdots, x_n, x'_1, \cdots, x'_n) \in A_1\times \cdots\times A_n\times A_1 \times \cdots\times A_n\\ \Define \cap_{(A_1, \cdots, A_n)}(x_1, \cdots, x_n, x'_1, \cdots, x'_n \mid *) := \delta( (x'_1, \cdots, x'_n), (x_1, \cdots, x_n) )$

評価〈余単位〉も同様です。

$\Declare \cup_{(A_1, \cdots, A_n)}: (A_1, \cdots, A_n, A_1, \cdots, A_n) \to () \:\text{ as tensor}\\ \Declare \cup_{(A_1, \cdots, A_n)}: (A_1\times \cdots\times A_n\times A_1\times \cdots\times A_n)\times \{*\} \to {\bf R} \:\text{ as function}\\ \For (x_1, \cdots, x_n, x'_1, \cdots, x'_n) \in A_1\times \cdots\times A_n\times A_1 \times \cdots\times A_n\\ \Define \cap_{(A_1, \cdots, A_n)}(*\mid x_1, \cdots, x_n, x'_1, \cdots, x'_n ) := \delta( (x'_1, \cdots, x'_n), (x_1, \cdots, x_n) )$

要するに、 $\I, \cap, \cup$ の定義は全部クロネッカーのデルタです。 $\mathrm{X}, \Delta, !$ は今回使わないので書き下しません。

ワイヤーベンディング・オペレーター

行列（特別なタイプのテンソルとみなす） $f$ から $f^\dagger$ を直接作ってもいいのですが、ここではワイヤーベンディング・オペレーターを適用して $f^\dagger$ を作ってみます。

プロファイルが $(A_1, \cdots, A_n) \to (B_1, \cdots, B_n)$ であるテンソルの全体の集合を ${\bf FXTens}( (A_1, \cdots, A_n), (B_1, \cdots, B_n))$ と書きます。"FX" は "eXtended tensors on Finite sets" からです。

$\quad f:(A_1, \cdots, A_n) \to (B_1, \cdots, B_n) \:\text{ as tensor}\\ \Iff f \in {\bf FXTens}( (A_1, \cdots, A_n), (B_1, \cdots, B_n))\\ \Iff f: (A_1\times \cdots\times A_n)\times (B_1\times \cdots\times B_n) \to {\bf R} \:\text{ as function}\\ \Iff f \in {\bf Set}( (A_1\times \cdots\times A_n)\times (B_1\times \cdots\times B_n), {\bf R})$

さて、下の絵で表されるオペレーター $\mathrm{ULBend}$ を考えます。この名前は "upper left bending" からなので、描画方向に依存したネーミングです。

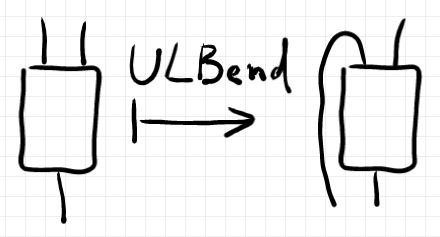
ULBendする前が $f:(A, B) \to (C)$ だとすると、ULBendした後は $\mathrm{ULBend}(f): (B) \to (A, C)$ になります。したがって、写像としての $\mathrm{ULBend}$ のプロファイルは：

$\quad \mathrm{ULBend}: {\bf FXTens}( (A, B), (C)) \to {\bf FXTens}( (B), (A, C))$

一般的な場合は：

$\quad \mathrm{ULBend}: {\bf FXTens}( (A_1, \cdots, A_n, B_1, \cdots, B_m), (C_1,\cdots, C_l)) \\ \qquad \to {\bf FXTens}( (B_1, \cdots, B_m), (A_n,\cdots, A_1, C_1, \cdots, C_l))$

$\mathrm{ULBend}$ は単一の写像なのではなくて、 $(A_1, \cdots, A_n), ( B_1, \cdots, B_m), (C_1,\cdots, C_l)$ ごとに存在する関数達の集まり、つまり総称関数〈多相関数〉です。そこまで正確に書けば：

$\quad \mathrm{ULBend}_{(A_1, \cdots, A_n), ( B_1, \cdots, B_m), (C_1,\cdots, C_l)}: {\bf FXTens}( (A_1, \cdots, A_n B_1, \cdots, B_m), (C_1,\cdots, C_l)) \\ \qquad \to {\bf FXTens}( (B_1, \cdots, B_m), (A_n,\cdots, A_1, C_1, \cdots, C_l))$

正確に書くと添字が鬱陶しいので、次のように略記します。

$\quad \mathrm{ULBend}_{(A_1, \cdots, A_n), ( B_1, \cdots, B_m), (C_1,\cdots, C_l)}(f) = \mathrm{ULBend}(f) = {^\cap f}$

最後の ${^\cap f}$ はもちろん象形文字です。特定のプロファイルに対して ${^\cap f}$ を書き下してみると：

$\quad \mathrm{ULBend}_{(A), (B), (C)}(f) = \mathrm{ULBend}(f) = {^\cap f} \\ := (\cap_{(A)} \otimes \I_{(B)}); (\I_{(A)}\otimes f)$

以下は、オペレーター $\mathrm{LRBend}$ （"lower right bending"）の絵です。もう同じことですね。

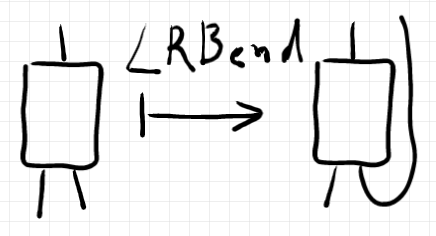
正確に書けば：

$\quad \mathrm{LRBend}_{(A_1, \cdots, A_n), ( B_1, \cdots, B_m), (C_1,\cdots, C_l)}: {\bf FXTens}( (A_1, \cdots, A_n), (B_1, \cdots, B_m, C_1,\cdots, C_l)) \\ \qquad \to {\bf FXTens}( (A_1,\cdots, A_n, C_l, \cdots, C_1), (B_1, \cdots, B_m) )$

略記は：

$\quad \mathrm{LRBend}_{(A_1, \cdots, A_n), ( B_1, \cdots, B_m), (C_1,\cdots, C_l)}(f) = \mathrm{LRBend}(f) = f_\cup$

特定のプロファイルに対して $f_\cup$ を書き下してみると：

$\quad \mathrm{LRBend}_{(A), (B), (C)}(f) = \mathrm{LRBend}(f) = f_\cup \\ := (f \otimes \I_{(C)}) ; (\I_{(B)} \otimes \cup_{(C)} )$

この節で紹介したワイヤーベンディング・オペレーターは、余評価／評価／恒等を組み合わせて具体的に書けます。マルコフ圏の条件化オペレーター（「マルコフ圏におけるベイズの反転定理」参照）やトレース付き圏のトレース・オペレーター（「トレース付き対称モノイド圏とはこんなモノ」参照）は、そのような具体的な表示を持ちません。

転置行列の構成

$f:A \to B$ が行列とします。行列は、プロファイルが単元リスト（長さ1のリスト）で与えられるようなテンソルと同一視します。つまり：

$\quad f:A \to B \:\text{ as matirx}\\ \Iff f\in {\bf FXMat}(A, B)\\ \Iff f:(A) \to (B ) \:\text{ as tensor}\\ \Iff f\in {\bf FXTens}( (A), (B) )\\ \Iff f: A\times B \to {\bf R} \:\text{ as function}$

ワイヤーベンディング・オペレーター $\mathrm{ULBend}$ と $\mathrm{LRBend}$ をこの順で適用すると転置になる（はず）ですが、それは次のように描けます。

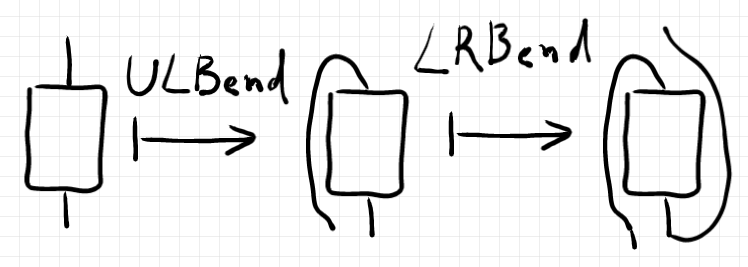
テキストで書くなら：

$\quad f^\dagger = (\mathrm{ULBend} ; \mathrm{LRBend} )(f) = \mathrm{LRBend}(\mathrm{ULBend}(f)) = ({^\cap f})_\cup$

$({^\cap f})_\cup$ を絵に描けば以下のようです。全体が $({^\cap f})_\cup$ で、濃いオレンジ色の枠で囲まれた部分が ${^\cap f}$ です。

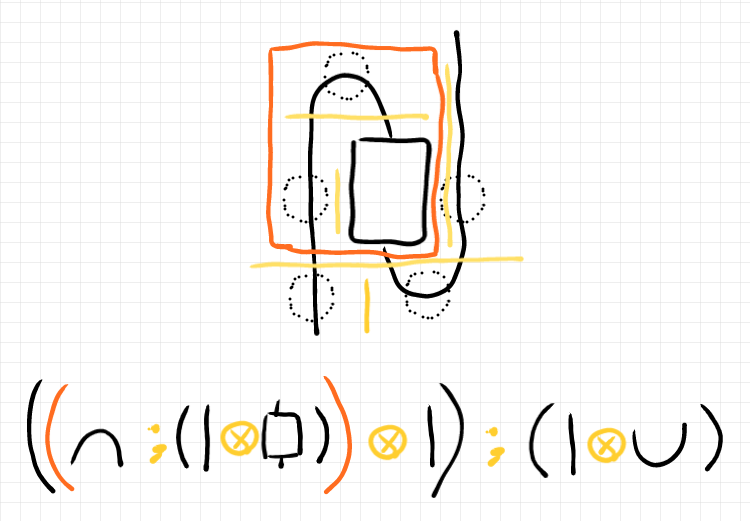
点線の丸の部分は余評価〈単位〉、評価〈余単位〉、恒等です。
黄色い縦棒はテンソル積を示します。
黄色い横棒は結合を示します。
下側は、ストリング図を色付き象形文字テキストに書き下したものです。

キーワードを使ったテキストで書くなら次のようです。

$\quad (( \mathrm{coev}_{(A)} ; (\id_{(A)} \otimes f ) \otimes \id_{(B)} ); (\id_{(A)} \otimes \mathrm{ev}_{(B)}) )$

それにしても、これがほんとに転置なの？

成分表示と計算

テキストによる計算を実行するために、絵の情報を写し取ります。バカ正直に写し取ると、たくさんの変数が必要になります。ここは実際にバカ正直に写し取るので、型 $A$ の変数を4個、型 $B$ の変数を3個確保します。変数は番号で識別することにして、次のように番号を付けます。

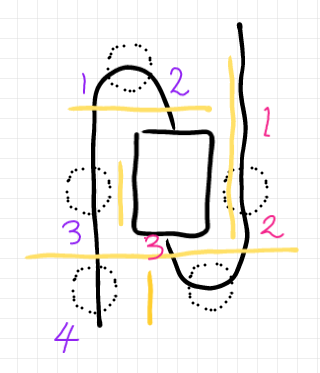
青紫が $x1, x2, x3, x4$
赤紫が $y1, y2, y3$

部品を列挙します。

$\quad \cap(x1, x2\mid *) = \mathrm{coev}(x1, x2 \mid *)\\ \quad \I(x3 \mid x1)\\ \quad f(y3 \mid x2)\\ \quad \I(y2 \mid y1)\\ \quad \I(x4 \mid x3)\\ \quad \cup(* \mid y3 , y2) = \mathrm{ev}(* \mid y3, y2)$

部品を結合とテンソル積で組み立てます。

$\sum_{x3, y3, y2}\big(\\ \quad ( \I(x4 \mid x3) \mathrm{ev}(* \mid y3 , y2) )\\ \quad \sum_{x1, x2}\big(\\ \qquad (\I(x3 \mid x1)f(y3 \mid x2) ) \, \mathrm{coev}(x1, x2\mid *) \\ \quad \big) \, \I(y2 \mid y1) \\ \big)$

これは文字通りバカ正直／バカ丁寧（やるヤツはバカ）で、通常はここまで律儀に写し取らないで適宜省略します。慣れれば、どこを省略できるかは分かるようになります。

定義により展開します。

$\sum_{x3, y3, y2}\big(\\ \quad ( \delta(x4, x3) \delta(y3 , y2) )\\ \quad \sum_{x1, x2}\big(\\ \qquad (\delta(x3, x1)f(y3 \mid x2) ) \, \delta(x1, x2) \\ \quad \big) \, \delta(y2, y1) \\ \big)$

ここからは、クロネッカーのデルタを消去する公式と（総和に関する）フビニの定理を使って計算するだけです。たくさんあるクロネッカーのデルタはことごとく消えてくれます。やってみましょう。

最後にもう一度注意しますが；ここまでのプロセスは過剰に丁寧な記述・計算です。うまくサボることにより、もっと素早く記述・計算する方法があります。上下の添字を巧みにあやつる“インデックス・ジャグリング”としての古典テンソル計算は、サボるテクニックを洗練させたものです -- 技法として見事だとは思いますが、「何やってるかワカラン」弊害もあります。「何やってるか」をクソバカ丁寧に追ってみると、この記事のような記述・計算になります。

[追記]
今回扱った転置の図で $f$ を恒等 $\I$ にすると、ワイヤーはうねったヘビの形になります。