図式思考の例として、コモノイドについて考えてみる - 檜山正幸のキマイラ飼育記 (はてなBlog)

セミナーでの話への補足なんですが、特別な話題ではなくて一般論なことなのでここに書きます。理解したり覚えたりする目的には、テキストで書かれた等式などは不向きであること、一方で具体的な表示・計算にはやはりテキストが有効であることを説明します。例として、集合圏内のコモノイドを取り上げます。 $\newcommand{\For}{\mbox{For}\:\:} \newcommand{\incat}{\:\: \mbox{in}\:}$

内容：

定義はどうせ覚えきれない
モノイドのイメージ
モノイドのひっくり返し
要素を追いかける
- 余結合法則
- 左余単位法則、右余単位法則
集合圏内のコモノイドとは何なのか
コモノイドはつまらないのか

定義はどうせ覚えきれない

フロベニウス代数／ホップ代数、あるいはモノイド圏／加群圏などの複雑な構造になると、その定義は（それぞれに）何十個かの等式（や同型関係式）*1で記述されます。それら何十個かの等式を書き下せと言われたら、僕は出来ません。そんなもん覚えてないし、記憶力に劣る僕が覚えられるわけないです。

しかし、ある程度の時間があれば定義を書き下せそうです。その時間は、翻訳に要する時間です。全然何も覚えてないわけじゃなくて、たくさんの等式とは“別な形“でイメージは持っています。そのイメージを何十個かの等式に翻訳すれば、オフィシャルな定義と同値な（まったく同じになるとは限らない）記述が得られるでしょう。

このような「イメージとテキストのあいだの翻訳」の例として、コモノイド〈余モノイド〉を取り上げます。僕は、「コモノイドはモノイドのひっくり返し」としか覚えていません。そのイメージから、具体的な等式を引っ張り出してみます。等式にすれば、具体的な計算が出来るというメリットがあります。具体的な計算により、集合圏におけるコモノイドの構造を完全に決定しましょう。

モノイドのイメージ

モノイドの法則を、ラフなストリング図で描けば次のようになります。

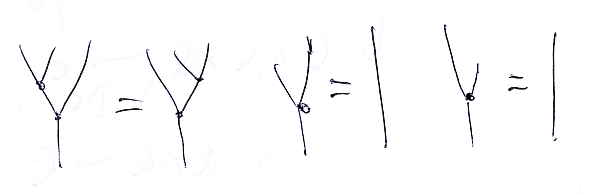
左から、結合法則〈結合律〉、左単位法則〈左単位律〉、右単位法則〈右単位律〉です。

ストリング図を描くツール／環境が整備されてないので、通常の文字組版・印刷やアスキーテキストでも実現できる代替表現として、次の方法があります。

ノード〈頂点 | 点〉の代わりに横線を描く。
ノードのラベルは横線の右脇に書く。
ワイヤー〈ストリング | 線〉は書かずに、ワイヤーのラベルだけを文字で書く。

この方法で、ラベル（集合と演算の名前・記号）をちゃんと書いてみます。

Aは集合。
Iは単元集合。太字の1を使わないのはアスキーテキストだけで書きたいから。Iの唯一の要素は何でもいいけど、今ここでは I = {0} とする。
mはモノイドの乗法 m:A×A→A 。
eはモノイドの単位 e:I→A 。

横線の脇に何も書いてないときは恒等写像だと思ってください。

結合法則
  A  A     A        A     A  A
 ------m  ---      ---   -----m
   A       A    =   A      A
  ----------m      ----------m
      A                A

左単位法則
        A        A
       ---      ---
  I     A        A
 ---e  ---  =   ---
  A     A        A
 --------m      ---
    A            A

右単位法則
  A              A
 ---            ---
  A    I         A
 ---  ---e  =   ---
  A    A         A
 --------m      ---
    A            A

集合Aの要素を取って、それを追いかけると：

結合法則
  x  y     z       x     y  z
 ------m  ---     ---   -----m
 m(x,y)    z   =   x    m(y,z)
  ----------m      -----------m
 m(m(x,y),z)       m(x,m(y,z))

左単位法則
        x        x
       ---      ---
  0     x        x
 ---e  ---  =   ---
 e(0)   x        x
 --------m      ---
 m(e(0),m)       x

右単位法則
  x              x
 ---            ---
  x    0         x
 ---  ---e  =   ---
  x   e(0)       x
 --------m      ---
 m(x,e(0))       x

最下段部分を取り出して、普通の等式として書けば：

結合法則： m(m(x,y),z) = m(x,m(y,z))
左単位法則： m(e(0),x) = x
右単位法則： m(x,e(0)) = x

e(0) を単に「e」と書いて、m を中置演算子記号「・」に書き換えれば、お馴染みの形になります。

結合法則： (x・y)・z = x・(y・z)
左単位法則： e・x = x
右単位法則： x・e = x

これらの等式は、僕でも覚えてはいますが、イメージから等式を引っ張り出すとは、こういうことです。

モノイドのひっくり返し

最初に出したラフなストリング図を、画像加工ソフトでミラーリング（鏡に写したような左右反転）してみます。

元画像

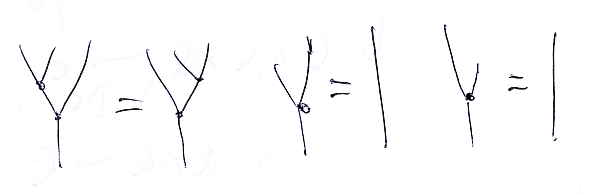
ミラー

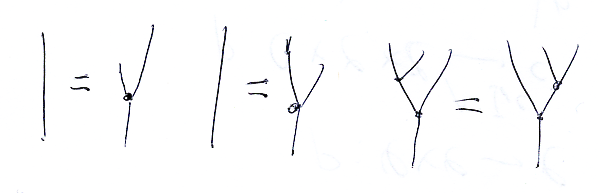
さらに180度回転します。

180度回転

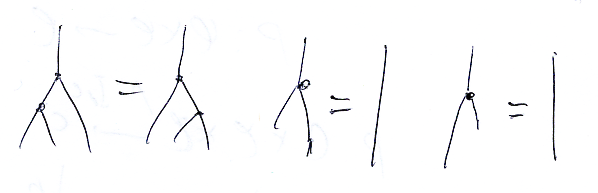
これが、コモノイド〈余モノイド | comonoid〉の法則を与えます。左から、余結合法則〈余結合律 | coassosiative law〉、左余単位法則〈左余単位律 | left counit law〉、右余単位法則〈右余単位律 | right counit law〉です

ラフな絵をもう少し詳しく描いてみます。赤字は説明の注釈です。右単位法則は省略しています（左単位法則と同様）。

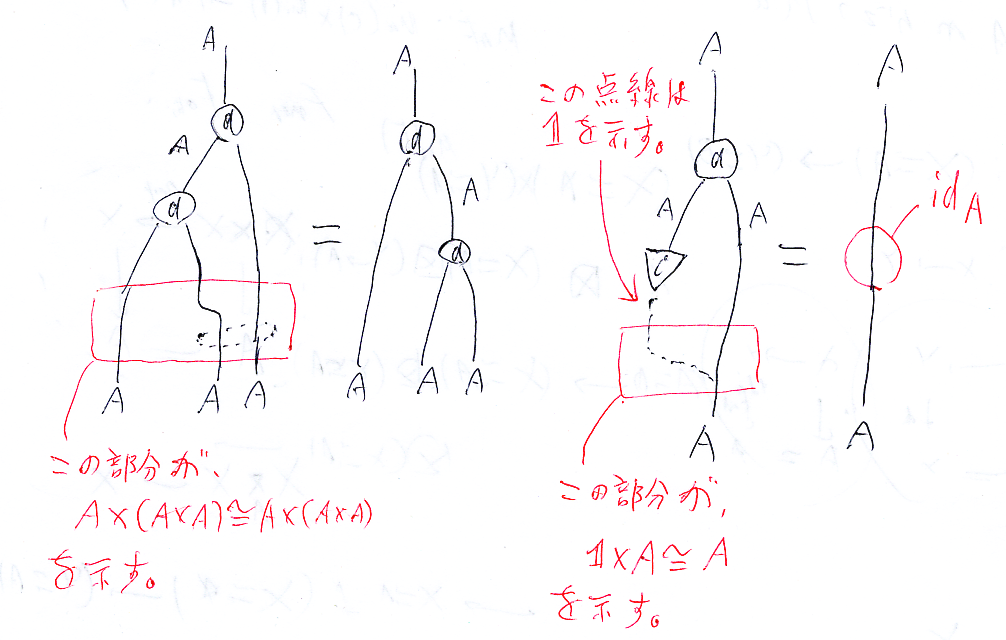
手書きなので読みにくいでしょうから、念の為：

オダンゴ（丸印）のなかは、d です。
三角印のなかは、i です。
赤字テキスト：この部分が、(A×A)×A $\cong$ A×(A×A) を示す。
赤字テキスト：この点線は 1 を示す。（今の約束だと 1 じゃなくて I ですね。失礼しました。）
赤字テキスト：この部分が、1×A $\cong$ A を示す。（同じく、1 じゃなくて I です。）
赤字テキスト： id_A

(A×A)×A $\cong$ A×(A×A) と I×A $\cong$ A を気にしないで（あたかもイコールだとみなして）、コモノイドの余結合法則と左余単位法則を可換図式で描けば：

$\require{AMScd} \begin{CD} A @>{d}>> A\times A \\ @V{d}VV @VV{id_A \times d}V \\ A\times A @>{d \times id_A}>> A\times A\times A \end{CD} \: \\ \: \\ \begin{CD} A @= A \\ @V{d}VV @| \\ A\times A @>{i \times id_A}>> A \end{CD}$

(A×A)×A $\cong$ A×(A×A) と I×A $\cong$ A を省略したのは、このブログで使える描画ツール（MathJax）が、多角形のレイアウトが出来ない、というショーモナイ理由です。四角形のレイアウトで我慢するなら：

$\require{AMScd} \begin{CD} A @>{d}>> A\times A \\ @V{d}VV @VV{id_A \times d}V \\ A\times A @. A\times (A\times A) \\ @V{d \times id_A}VV @| \\ (A\times A)\times A @>{\cong}>> A\times (A\times A) \end{CD} \: \\ \: \\ \begin{CD} A @= A \\ @V{d}VV @A{\cong}AA \\ A\times A @>{i \times id_A}>> I\times A \end{CD}$

描画や印刷の都合から、泣く泣く不正確でショーモナイ絵になってしまうことはよくあります（「絵算の威力をお見せしよう // 絵算の問題点」参照）。あと、「もう、めんどくせー」という理由で不正確でショーモナイ絵を描くことはもっとよくあります。とてもよくあります。

要素を追いかける

集合圏内のコモノイドは、集合と写像から組み立てられているので、集合の要素が、写像でどう移り変わるかを追いかけることができます。これもまずは、図の上で追いかけてみます。先程のストリング図と、要素追いかけの図を並べて掲げます。

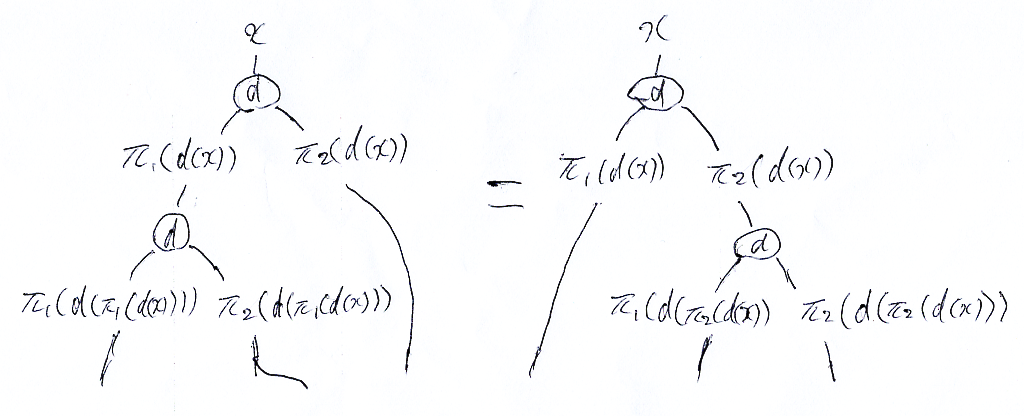
説明しましょう。d(x) は、x∈A に対するdの値で d(x)∈A×A です。となると、d(x) は要素のペア（長さ2のタプル）です。成分に分解するために、第一射影 π₁:A×A→A と第二射影 π₂:A×A→A を使います。

余結合法則

余結合法則左辺の上段部分を見ると、入出力は：

A∋ x $\mapsto$ (π₁(d(x)), π₂(d(x))) ∈A×A

余結合法則左辺の下段部分を見ると、入出力は：

A×A∋ (π₁(d(x)), π₂(d(x))) $\mapsto$ (π₁(d(π₁(d(x))), π₂(d(π₁(d(x))), π₂(d(x))) ∈A×A×A

正確に言えば、(A×A)×A∋ ((a, b), c) $\mapsto$ (a, (b, c)) ∈A×(A×A) の写像もありますが、まー、いいとしましょ。

結局、余結合法則左辺の要素の変化は次のようになります。

A∋ x $\mapsto$ (π₁(d(π₁(d(x))), π₂(d(π₁(d(x))), π₂(d(x))) ∈A×A×A

同様にして、余結合法則右辺の要素の変化は次のようになります。

A∋ x $\mapsto$ (π₁(d(x)), π₁(d(π₂(d(x))), π₂(π₁(d(x))) ∈A×A×A

よって、余結合法則の等式表現は次のようになります。

(π₁(d(π₁(d(x))), π₂(d(π₁(d(x))), π₂(d(x))) = (π₁(d(x)), π₁(d(π₂(d(x))), π₂(π₁(d(x))) on A×A×A

"on A×A×A" は、「等式は A×A×A 上で成立する」という注釈です。連立方程式に分解すれば：

π₁(d(π₁(d(x))) = π₁(d(x)) on A
π₂(d(π₁(d(x))) = π₁(d(π₂(d(x))) on A
π₂(d(x)) = π₂(π₁(d(x)) on A

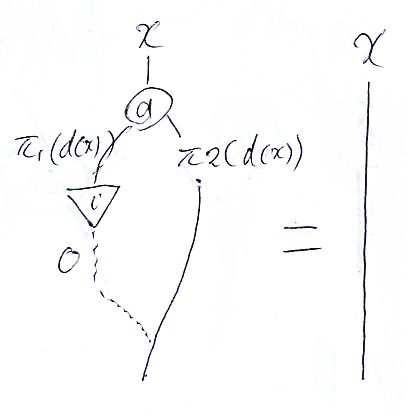
左余単位法則、右余単位法則

次に、左余単位法則の図を見ましょう。i は、i:A→I という写像ですが、I は単元集合 {0} だったので、i(x) = 0 という写像しかありません。余単位 i は一択で確定してしまうのです。

x $\mapsto$ (π₁(d(x)), π₂(d(x))) の後で、ペアの第一成分は 0 に潰されて (0, π₂(d(x))) となり、(0, a) $\mapsto$ a により π₂(d(x)) だけが取り出されます。結局、余単位法則の左辺は、

A∋ x $\mapsto$ π₂(d(x)) ∈A

右辺はもちろん、

A∋ x $\mapsto$ x ∈A

よって、左余単位法則の等式が言っていることは、

π₂(d(x)) = x on A

同様にして、右余単位法則からは、

π₁(d(x)) = x on A

が出ます。

集合圏内のコモノイドとは何なのか

前節最後の等式をもう一度見てみましょう。

π₁(d(x)) = x on A
π₂(d(x)) = x on A

dはコモノイドの余乗法でした。これらの等式の言っていることは：

余乗法（の出力）の第一成分は入力に等しい。
余乗法（の出力）の第ニ成分は入力に等しい。

つまり、コモノイド余乗法とは、入力を複製したペアを作ることです。それ以外の可能性は、左余単位法則／右余単位法則から禁止されてしまいます。

複製操作〈duplication | copy〉が余結合法則を満たすことは明らかですから、次のことが分かります。

複製操作を余乗法に選ぶと、任意の集合上にコモノイドを構成できる。
コモノイドの余乗法は、複製操作以外にはあり得ない。

既に述べたように、余単位は選択の余地がなく決まってしまいます。そこから余乗法も選択の余地がなくなります。ということは、任意の集合 A に対して、A を台集合〈underlying set〉とするコモノイド構造が常にひとつだけ確定するのです。

我々は、任意の集合に対して（それを台集合とする）コモノイドを作る手順を知りました。この手順は標準的〈canonical〉、あるいは自然〈natural〉です。「標準的／自然」はテクニカルタームで、コモノイドの演算である余乗法と余単位が自然変換になっていることです。このことを説明しましょう。

ここからは、世間の習慣に従って、コモノイド余乗法を Δ、コモノイド余単位を ! という記号で表します。

Δ(x) = (x, x) （複製操作）
!(x) = 0 （破棄操作）

集合Aごとに Δ, ! が決まるので、次の書き方をします。

Δ_A:A→A×A （Aにおける複製操作）
!_A:A→I （Aにおける破棄操作）

ここで出てきた Δ_A と !_A は、ほんとに自然変換になっているのでしょうか。

自然変換は関手のあいだの変換ですから、先に関手を設定する必要があります。次の関手を準備します。

Id:Set→Set ： Id(A) := A, Id(f:A→B) := (f:A→B)
D:Set→Set ： D(A) := A×A, D(f:A→B) := (f×f:A×A→B×B)
K:Set→Set ： K(A) := I, K(f:A→B) := (id_I:I→I)

この設定のもとで、Δ = (Δ_A:Id(A)→D(A) | A∈Obj(Set)) と ! = (!_A:Id(A)→K(A) | A∈Obj(Set)) は、次のような自然変換であることは容易に確認できます。

Δ::Id⇒D:Set→Set
!::Id⇒K:Set→Set

容易な確認とは、次のような自然性を表す図式を書いて、図式が実際に可換となることを確認することです。

$\For f:A \to B \incat {\bf Set} \\ \begin{CD} Id(A) @>{\Delta_A}>> D(A) \\ @V{Id(f)}VV @VV{D(f)}V \\ Id(B) @>{\Delta_B}>> D(B) \end{CD} \: \\ \: \\ \begin{CD} Id(A) @>{!_A}>> K(A) \\ @V{Id(f)}VV @VV{K(f)}V \\ Id(B) @>{!_B}>> K(B) \end{CD} \\ \mbox{commute in}\:\: {\bf Set}$

Id, D, K を定義により置き換えてしまえば、

$\For f:A \to B \incat {\bf Set} \\ \begin{CD} A @>{\Delta_A}>> A\times A \\ @V{f}VV @VV{f \times f}V \\ B @>{\Delta_B}>> B\times B \end{CD} \: \\ \: \\ \begin{CD} A @>{!_A}>> I \\ @V{f}VV @VV{id_I}V \\ B @>{!_B}>> I \end{CD} \\ \mbox{commute in}\:\: {\bf Set}$

当たり前に見えるでしょ。

集合ごとにコモノイドを構成する方法は、いきあたりばったりなのではなくて、2つの自然変換により与えられる系統的な手順なのです。

コモノイドはつまらないのか

「なーんだ、コモノイドって複製のことなのか、つまらん」と思われた方もいるでしょう。実際、単純な結論になっています。しかし、コモノイド上の余加群まで考えると、メモリーやデータベースなどのストレージの代数的モデルができたりします。

このブログ内、「余加群」の検索結果

集合圏のコモノイドは複製に限るのですが、他の圏では事情が変わります。同じ概念でも、環境となる圏（いわば世界）が変わればまったく様変わりしてしまうことは多いのです。例えば、（適当な体上の）ベクトル空間の圏Vectのなかで、コモノイドを考えると、それは余代数〈coalgebra〉になります。集合圏とは違って、ベクトル空間の圏のコモノイドである余代数には、様々なバリエーションがあります。

モノイドとコモノイドの両方の構造を持つ対象は双モノイドと呼びます。ベクトル空間の圏の双モノイドは双代数です。冒頭で名前だけ出したフロベニウス代数やホップ代数は、代数（ベクトル空間の圏内のモノイド）／余代数（ベクトル空間の圏内のコモノイド）／双代数（ベクトル空間の圏内の双モノイド）といった構造を扱う文脈において登場します。

このブログ内、「双代数」の検索結果

とある構造を表す図式（可換図式やストリング図）をひっくり返すだけで、新しい構造を定義できます。単にひっくり返しただけですから、覚える負担もありません。もとの構造とひっくり返した構造は、似ても似つかないことがあります。形式的ひっくり返しで、内容的には全然別な物が現れるのがひっくり返し（双対性）の面白いところです。

ひっくり返しをするためには、まずは図式を描きます。それに、ミラーリングや回転をします。ミラーリングや回転が苦手な人（僕は苦手です）は、トレーニングしましょう。

双対や随伴に強くなるためのトレーニング

*1:何十個と言っても、80個、90個ってことはないです。一桁じゃきかない、という程度の意味。