ユークリッド空間に埋め込まれた向き付き多様体の向きの表現法

※ 追記あります。

ジョニー（a.k.a. id:hiroki_f @hiroki_f）*1が、twitterで「埋め込まれた多様体の向き」のことをつぶやいていたのですが、最初、意味がよく分かりませんでした（ツイートなので致し方ない）。2,3度やり取りして、だいたい納得しました。

まさにそういうことです！
— Hiroki Fukagawa (@hiroki_f) 2020年6月14日

n次元多様体N（最近は、次元と多様体の名前を同じ文字で揃えたい）には向きが決まっているとします。m次元ユークリッド空間R^mにも標準的な向きが決まっています。R^m上の標準的な微分形式 $dx^1, \cdots, dx^m$ は、この順で、余接ベクトルバンドルの正のフレーム〈向きと同調した順序基底〉になっています*2。

ジョニーのツイートは、埋め込み f:N→R^m （n < m）があるとき、Nの（あるいは埋め込み像 f(N)⊆R^m の）向きを $dx^1, \cdots, dx^m$ を使って書き表したい、ということだろうと理解しました。

埋め込み像 f(N) の外の点（ $x\in \mathbf{R}^m, \: x \notin f(N)$ な点）で何らかの量を考えてもしょうがなさそうなので、f(N) あるいはもとの N 上の量を $dx^1, \cdots, dx^m$ で書き表す、ということでしょう、たぶん。

必ずしもユークリッド空間とは限らないm次元多様体Mを埋め込み先として考えることにして、f:N→M が埋め込みだとします。fの接写像を取ると、Tf:TN→TM 、TMをfでN上に引き戻したベクトルバンドルを f^#TM として、Tf に対応するN上のバンドル射を Df とします。次の可換図式があります。

$\require{AMScd} \begin{CD} TN @>Df>> f^\# TM \\ @V{\pi}VV @VV{\pi}V \\ N @= N \\ \end{CD}$

ファイバーごとに空間も写像も双対を取ります*3。

$\require{AMScd} \begin{CD} (f^\# TM)^\ast @>{Df^\ast}>> (TN)^\ast \\ @V{\pi}VV @VV{\pi}V \\ N @= N \\ \end{CD}$

外積の意味でn乗します*4。

$\require{AMScd} \begin{CD} \bigwedge^n( (f^\# TM)^\ast ) @>{\bigwedge^n(Df^\ast)}>> \bigwedge^n( (TN)^\ast) \\ @V{\pi}VV @VV{\pi}V \\ N @= N \\ \end{CD}$

ここで、 $\bigwedge^n( (TN)^\ast)$ はファイバー次元1のバンドル（直線バンドル）で、ゼロを取り除くと、ファイバーは2つの連結成分に別れます。どっちか片方の連結成分を大域的に選ぶことがNに向きを与えることです*5。

線形代数の準同型定理（のベクトルバンドル版）から、次の同型が言えます。

$\bigwedge^n( (f^\# TM)^\ast )/Ker(\bigwedge^n(Df^\ast) ) \cong \bigwedge^n( (TN)^\ast)$ as vector bundles over $N$

両辺のファイバーごとの次元を比較すると、核バンドル $Ker(\bigwedge^n(Df^\ast))$ は、余次元1の部分バンドル、つまり $\bigwedge^n( (f^\# TM)^\ast )$ 内の超平面バンドルです。超平面 $Ker(\bigwedge^n(Df^\ast))$ を取り除くと、 $\bigwedge^n( (f^\# TM)^\ast )$ のファイバーは2つの連結成分（半空間）に別れます。どっちか片方の連結成分を大域的に選ぶことがNに向きを与えることです。

Nの向きの指定は、 $\bigwedge^n( (f^\# TM)^\ast ) \setminus Ker(\bigwedge^n(Df^\ast))$ （ $\setminus$ は集合の差）のファイバー連結成分の指定になったわけですが、そのためには、超平面 $Ker(\bigwedge^n(Df^\ast))$ への法ベクトルを使えばいいでしょう。もし、 $\bigwedge^n( (f^\# TM)^\ast )$ が内積ベクトルバンドルの構造を持てば、超平面 $Ker(\bigwedge^n(Df^\ast))$ に直交する単位ベクトル（の場）を使えます。

M = R^m の場合、 $\bigwedge^n( (f^\# TM)^\ast ) = \bigwedge^n( (f^\# T{\bf R}^m)^\ast )$ はN上の自明バンドルになり、標準的フレーム〈順序基底〉は、 $dx^1, \cdots, dx^m$ 達からn個選んで外積したn次形式達として具体的に列挙できます。また、外積空間に内積も入ります。したがって、超平面 $Ker(\bigwedge^n(Df^\ast))$ への直交単位ベクトル（の場）も、 $dx^1, \cdots, dx^m$ 達の外積と1次結合で書き下せます。ただし $dx^1, \cdots, dx^m$ 達はR^mからNに引き戻されたものです。

これで一応、埋め込まれたNの向きを $dx^1, \cdots, dx^m$ 達で書き表せたことにはなるのだけど、カッコイイかどうかは分からない。どっちかというとウザイ表示な気がする。

[追記 date="翌日"]

面白い例は作れないのですが、特別に簡単な例を紹介しましょう。引き続き dim(N) = n, dim(M) = m 、n < m で、f:N→M は埋め込みだと仮定します。n + 1 = m 、つまり余次元1の埋め込みは話が簡単になります。特に、n = 2, m = 3, M = R³ のケースは伝統的かつ直感的です。

N = S² を、外の空間なしで与えられた球面（2次元多様体）として、その埋め込み像 f(S²)⊆R³ は原点中心半径10の球面だとします。半径をデカめに取っているのは、単位法ベクトル場との絵的バランスの関係です。

S²が（内在的に）持つ向きは、R³に埋め込まれた f(S²) の各点に単位法ベクトルを立てれば表現できます。外向き法ベクトル場か、内向き法ベクトル場のどちらかです。（下の絵はS¹の絵だけど。）

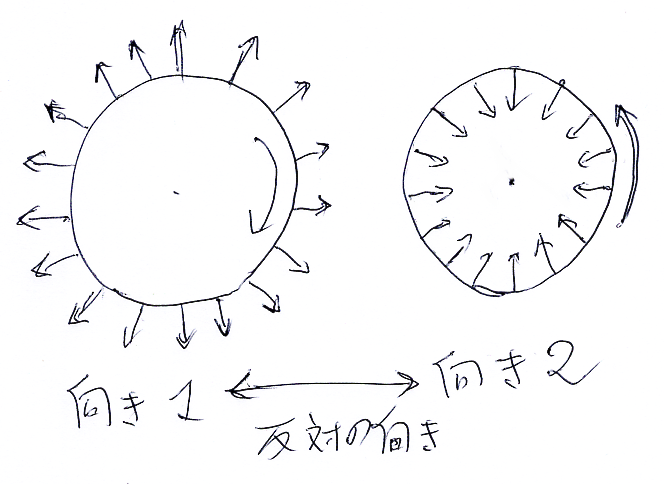
まず、引き戻しバンドル $f^\# (T{\bf R}^3) \mbox{ over } S^2$ がどんなものか説明します。これは、自明ベクトルバンドルで、S² の各点ごとにR³（正確に言えば、TR³のファイバー）を1個ずつひっ付けたものです。各R³は標準フレームを備えているので、それを $X_1, X_2, X_3$ としましょう。 $X_1, X_2, X_3$ は3つのベクトル場（S²の接ベクトル場ではない！）とみなせます。また、各点pごとにフレーム $(X_1(p), X_2(p), X_3(p))$ がひっ付いていると見れば、大域フレーム場（フレームバンドルの大域セクション）とも言えます。

双対なベクトルバンドル $(f^\# ( T{\bf R}^3) )^\ast \cong f^\# ( (T{\bf R}^3)^\ast) = f^\# (T^\ast{\bf R}^3) \mbox{ over } S^2$ は、 $dx^1, dx^2, dx^3$ で張られる自明ベクトルバンドルです*6。双対ペアリング〈スカラー積〉を $\langle \mbox{-} \mid \mbox{-} \rangle$ とすると：

$\mbox{For-all }p\in S^2,\; \langle dx^i \mid X_j \rangle_p = \delta^i_j \mbox{ where }i, j = 1, 2, 3$

R³ではなくてS²に引き戻して（あるいは、f(S)に制限して）考えていることに注意してください。

S²に局所座標〈チャート〉(U, s) を取りましょう。 $s^1, s^2:S^2 \supseteq U \to {\bf R}$ を座標関数とします。 $S_1 = \frac{\partial}{\partial s^1}, S_2 = \frac{\partial}{\partial s^2}$ と $ds^1, ds^2$ はそれぞれ、 $TS^2, T^\ast S^2$ の局所フレームになり、互いに相反〈双対〉なフレームです。

$s^1, s^2, x^1, x^2, x^3, S_1, S_2, X_1, X_2, X_3, ds^1, ds^2, dx^1, dx^2, dx^3$ を使えば、諸々の量を露骨に〈explicitly〉局所表示可能です（やらないけどね）。でも、露骨な表示（ヤコビアン）だと、 $Df:TN \to f^\# (T{\bf R}^3)$ と $Tf:TN \to T{\bf R}^3$ は区別できません。また、双対 $Df^\ast = (Df)^\ast : (f^\# (T{\bf R}^3) )^\ast \to (TN)^\ast$ も同じ行列（ときに転置行列）で表現できるので区別しにくいですね。ここらへんが座標を使った計算の嫌なところです。

肝心のS²の向きですが、局所的には $ds^1 \wedge ds^2$ を選ぶか、それとも $ds^2 \wedge ds^1 = - ds^1 \wedge ds^2$ を選ぶかで向きが決まります。局所的な選択をうまく繋げば大域的な向きの指定になります。これは、ファイバー1次元の外積ベクトルバンドル $\bigwedge^2( T^\ast S^2)$ の零点を持たない大域セクションの指定に他なりません。

本文（追記前の記事）の処方箋に従うと、 $Df^\ast: f^\# (T^\ast{\bf R}^3) \to T^\ast N$ *7を、2階外積ベクトルバンドルに持ち上げて $\bigwedge^2(Df^\ast): \bigwedge^2(f^\# (T^\ast{\bf R}^3)) \to \bigwedge^2( T^\ast N)$ を作るのでした。ここで、 $\bigwedge^2(f^\# (T^\ast{\bf R}^3))$ は、フレーム $dx^1\wedge dx^2,\; dx^2\wedge dx^3,\; dx^3\wedge dx^1$ で張られるファイバー3次元のベクトルバンドルです。

ベクトルバンドル写像の核ベクトルバンドル $Ker(Df^\ast)$ は、ファイバー3次元のベクトルバンドル $\bigwedge^2(f^\# (T^\ast{\bf R}^3) )$ 内のファイバー2次元の部分ベクトルバンドルです。2次元部分ベクトル空間は、3次元ベクトル空間を二つに分断します。分断されたどっち側かを指定することは、 $Ker(Df^\ast)$ の補ベクトル場〈complementary vector field〉（超平面の補空間を張るベクトル場）を指定するのと同じです。ベクトルバンドルが内積を持つなら、補ベクトル場として単位法ベクトル場（長さ1で超平面に直交するベクトルの場）を選べます。

というわけで、S²上のファイバー3次元のベクトルバンドル $\bigwedge^2(f^\# (T^\ast{\bf R}^3) )$ の適切なベクトル場〈セクション〉がS²の向きを表現することになります。ホッジ双対により、 $\bigwedge^2(f^\# (T^\ast{\bf R}^3))$ は $\bigwedge^1(f^\# (T^\ast{\bf R}^3) ) = f^\# (T^\ast{\bf R}^3)$ と同型であり、内積により $f^\# (T^\ast{\bf R}^3) \cong f^\# (T{\bf R}^3)$ です。ベクトルバンドルが同型ならセクション空間も同型になるので：

$\:\:\:\: \Gamma(\bigwedge^2(f^\# (T^\ast{\bf R}^3) ) ) \\ \cong \Gamma(f^\# (T^\ast{\bf R}^3) ) \\ \cong \Gamma(f^\# (T{\bf R}^3))$

本来、S²の向きは $\bigwedge^2(f^\# (T^\ast{\bf R}^3) )$ のベクトル場〈セクション〉で表現されますが、我々は $f^\# (T{\bf R}^3)$ のベクトル場〈セクション〉として捉えます（そのほうが分かりやすいので）。さらに、抽象的な多様体S²ではなくて、目に見える図形 f(S²)⊆R³ を想定して、逆立った毛〈法ベクトル〉が生えた球面の絵を描くわけです（皆さん、描いてください）。