このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

余次元1の埋め込みの向き

雑記／備忘

多様体の向きに関しては、「多様体の向き：色々な定義」に書いた、外積代数バンドルを使う向きの定義がスッキリしている気がします。が、しかし：

ところで、「0次元多様体は向き付け不可能なのでは」で触れた法直線バンドル／法ベクトル場を使った向きの定義も、捨てがたいものがあります。超曲面〈超部分多様体〉や境界を扱う場合は、法直線バンドル／法ベクトル場の方法が良さそうです。

僕の好みだけの問題かも知れませんが、法直線バンドル／法ベクトル場を使う方法は、幾何的イメージがハッキリしている点がいいな、と感じます。ただし注意すべきは、法直線バンドル／法ベクトル場により定義される向きは、多様体それ自体の性質／構造ではないことです。多様体のあいだの埋め込みに対して定義される性質／構造です。多様体の性質／構造と、写像の性質／構造が峻別できてないと混乱するかも知れません。

なお、この記事内で出てくる「大域フレーム{場}?」のような表現は、「場」を省略可能なことを表します。詳しいことは次の記事に書いてあります。

内容：

基本的な概念

バラバラと用語の定義を書き並べます。定義を理解するには、より基本的な知識が必要ですが、そこまでは説明してません（前提とする）。面白みのない列挙で恐縮です。

単に多様体〈manifold〉といった場合は、境界を許すなめらかな多様体で、多様体のあいだの写像〈map | mapping | homomorphism | morphism〉はなめらかな写像のことです。f:M→N が、f(∂M)⊆∂N のとき境界を保存する〈preserve boundary〉といいますが、一般的写像にこの条件は要求しません。

階数〈rank | ファイバー次元〉が1のベクトルバンドルを直線バンドル〈line bundle〉と呼びます。

多様体M上のベクトルバンドルEのフレームバンドルを frame(E) と書き、その大域セクションの空間は ΓM(frame(E)) と書きます。ΓM(frame(E)) の要素を次のように呼びます（すべて同義語と思ってよい*1）。

  1. Eの大域自明化〈global trivialization〉
  2. Eの大域フレーム{場}?〈global frame {field}?〉
  3. Eのフレーミング〈framing〉
  4. Eの平行化〈parallelization〉

平行化という言葉を使うならば、ベクトルバンドルの平行化可能性は次のように定義できます：

  • Eは平行化可能〈parallelizable〉 :⇔ ΓM(frame(E)) ≠ ∅

大域自明化可能〈globally trivializable〉でも、平行化可能と同義です。なんの事情なのか、このへんは同義語・類義語が溢れかえっています。鬱陶しい。

ベクトルバンドル E とセクション ψ∈ΓM(frame(E)) の組 (E, ψ) を、平行化済みベクトルバンドル〈parallelized vector bundle〉または{大域}?フレーム付きベクトルバンドル〈{globally}? framed vector bundle〉と呼びます。

フレームバンドル frame(E) に群Gが作用していて、商を取ったバンドル frame(E)/G を考えることがよくあります。多様体の向きの定義（のひとつ）もそのように考えました。frame(TM)/GL+(m) のセクションが多様体Mの向きでした（「0次元多様体は向き付け不可能なのでは」参照）。

f:M→N が多様体のあいだの写像だとして、fが埋め込み〈embedding〉であるとは、次の条件を満たすことです*2。

  1. fは写像として単射である。
  2. 各点での接写像 TpM→Tf(p)N が単射線形写像である。

MからNへの埋め込みの全体を Emb(M, N) と書きます。MからNへの埋め込みが存在しないこともあるので、Emb(M, N) が空集合であることもあります。f∈Emb(M, N) に対して、dim(N) - dim(M) を埋め込みの余次元〈codimension〉と呼びます。

埋め込み f:M→N が次の条件も満たすとき、局所同型埋め込み〈locally isomorphic embedding〉または開埋め込み〈open embedding〉と呼びます。

  • 各点での接写像 TpM→Tf(p)N が双射線形写像〈可逆線形写像〉である。

局所同型埋め込みが、実際に局所同型になることは、逆関数定理から出ます。局所同型埋め込みは、開集合を開集合に移す性質を持ちます（ゆえに開埋め込み）。“局所同型埋め込み＝開埋め込み”の余次元は0です。

埋め込みの法バンドル

M, X が多様体で、i;M→X は埋め込みだとします。i# は、ベクトルバンドルの引き戻しを表します。X上にベクトルバンドル F があると、i#F = i#(F) は、M上のベクトルバンドルになり、(i#F)p = Fi(p) が成立します。

埋め込み i:M→X を (M, i) とも書くことにして、埋め込みの法{ベクトル}?バンドル〈normal {vector}? bundle〉 N(M, i) を次のように定義します。

  • N(M, i) := (i#TX)/TM

これは、M上の2つのベクトルバンドル i#TX と TM の商ベクトルバンドルです。点 p∈M ごとに、(TM)p⊆(i#TX)p という部分空間の関係があるので、点ごとに商ベクトル空間を作り、それらを束ねたバンドルが (i#TX)/TM です。MとXにリーマン計量があるのならば、部分空間の直交補空間のバンドルとして法バンドルを実現することができます。

M上のベクトルバンドルの圏内に、次の完全列が作れます。

\require{AMScd} \begin{CD} 0 @>>> TM @>Di>> i^{\#}TX @>>> N(M, i) @>>> 0 \\ \end{CD}

Diは、iの“微分”で、接写像 Ti:TM→TX の TX をM上に引き戻したものです*3。

法バンドルに関連して、管状近傍定理を紹介しておきます*4。埋め込みの像（埋め込み先Xの部分多様体）のタチの良い開近傍として、埋め込みの法バンドルの凸近傍と位相同型な開集合（それを管状近傍と呼ぶ）が取れることを主張する定理です。

EはM上のベクトルバンドルとして、0M:M→E は、Mの点をファイバーのゼロベクトルに写すゼロセクションとします。ゼロセクションとゼロセクションの像を区別しないことが多いですが、ここでは、ZeroM = ZeroME = Im(0M) ⊆ E と書くことにします。セクション 0M:M→E も、部分多様体 ZeroM⊆E も、呼び名はゼロセクション〈zero section〉です（要注意）。

ZeroM ⊆ C ⊆ E である開集合Cが、Eの（ゼロセクションの）凸近傍〈convex neighborhood〉だとは、Cが局所的には U×D の形をしていることです。ここで：

  • U⊆M は開集合
  • VをEの典型ファイバー・ベクトル空間として、D⊆V はゼロを含む凸開集合

特に、開凸集合 D を Rr（rはファイバー次元）の単位開円板〈単位開球体〉に取ることができます。

管状近傍定理〈tubular neighborhood theorem〉の主張は、埋め込み i:M→X に対して、法バンドル N(M, i) の凸近傍Cへの i の拡張 j:C→X で、Cとj(C) が位相同型となるものが存在する、ということです。j(C)⊆X はXの開集合で i(M) を含むので、i(M) の開近傍になります。そして、Cと同じ形をしています。j(C) として与えられる i(M) の開近傍を、管状近傍〈tubular neighborhood〉といいます。

次の可換図式が、管状近傍定理の状況を表しています。ラベルがない矢印は包含写像です。

\require{AMScd} \begin{CD} M @>i>> i(M) @>>> X \\ @V{0_M}VV @VVV @| \\ C @>j>> j(C) @>>> X \\ @VVV @. @. \\ N(M, i)@. {} @. {} \\ \end{CD}

次の図は、M = [0, 1] ⊆ R, X = R2 のときの管状近傍の例です。

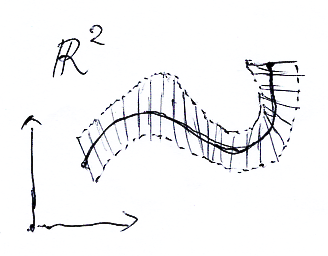
超曲面埋め込みの向き

余次元が1の埋め込み i:M→X を超曲面埋め込み〈hypersurface embedding〉とも呼びます。「曲面」は部分多様体の意味で、次元が2とは限りません。余次元1の部分ベクトル空間（または部分アフィン空間）を、次元が何であれ超平面と呼ぶのと同様です。

超曲面埋め込み i:M→X が向き付け可能〈orientable〉だとは、次の条件を満たすことです。

  • 超曲面埋め込みの法バンドル N(M, i) が平行化可能である。

i の余次元が1であることから、法バンドル N(M, i) は直線バンドルになります。平行化可能の定義から、次のように言っても同じです。

超曲面埋め込みの向き付け可能性には、MとXの（多様体としての）向き付け可能性や向きは一切関与してません。前もって、MやXに（多様体としての）向きを与える必要はないし、MもXも向き付け不可能であっても、i:M→X が向き付け可能になることはあります。

超曲面埋め込み (M, i) が向き付け可能ならば、法バンドル N(M, i) は“大域フレーム＝フレーミング”を持つので、セクション空間 ΓM(N(M, i)) は空ではありません。ΓM(N(M, i)) に次の関係をいれます。

  • For s, t∈ΓM(N(M, i)),
    s ～ t :⇔ (s = t・r となる r∈C∞(M, R+) が存在する)

ここで、'・'はスカラー倍で、R+ は正実数の集合です。～ は同値関係となり、商集合を作れるので、超曲面埋め込み (M, i) の向きの集合を次のように定義します。

  • Or(M, i) := ΓM(N(M, i))/～

これは、次の定義でも同じです。

  • Or(M, i) := ΓM(N(M, i)/R+)

ここで、R+ は正実数の掛け算の群で、1次元ファイバーにスカラー倍として作用します。商（スラッシュ記号）は、この群作用による商です。

Mが連結多様体で、超曲面埋め込み (M, i) が向き付け可能なとき、向きの集合 Or(M, i) は二元集合になります。連結でないときは、各連結成分ごとに2つの向きがあります。

多様体の向きと超曲面埋め込みの向きは違うものですが、直線バンドルのセクション空間が鍵となっている点は類似しています。多様体の連結成分ごとに2つの向きがあることは、直線から原点〈ゼロ〉を除くと、2つの部分に分かれることが背景にあります。

多様体の向きと超曲面埋め込みの向き

古典的曲面論では、2次元多様体Mを調べる際に、i:M→R3 という超曲面埋め込みを使っていました。2次元多様体Mの性質／構造と、超曲面埋め込み i の性質／構造が分離されていなかったので、「向き」の概念が「何に対して定義されるか」が不明確になってしまったのでしょう（たぶん*5）。

超曲面埋め込みに対して「向き付け可能」「向き」という用語を使い続けると、混乱を助長するので、一時的に用語を変更します。

  • 超曲面埋め込みが向き付け可能 → 超曲面埋め込みが法平行化可能〈normally parallelizable〉
  • 超曲面埋め込みの向き → 超曲面埋め込みの法フレーミング〈normal framing〉

normal, normally （「正規」「正常」と解釈できる）を使うのが、そもそも誤解を招くのですが、直交〈orthogonal〉、垂直〈perpendicular〉を使うと計量の存在を暗示してしまうし、ベクトルバンドルの作り方から商〈quotient〉とか補〈complement〉とか付けたら一般的過ぎるし。致し方ないので、「法〈normal〉」は使い続けます。

さて、超曲面埋め込み i:M→X が法平行化可能だとします。つまり、超曲面埋め込みの法バンドル〈法直線バンドル〉N(M, i) はフレーミング〈大域フレーム | 大域自明化〉を持ちます。法バンドルのフレーミングを法フレーミングと呼ぶのでした。法平行化可能埋め込みは、法フレーミングをたくさん持つかも知れません。ひとつの法フレーミングnを選んで固定した組 (M, i, n) を法フレーミング付き埋め込み〈normal framed embedding〉と呼びましょう。ひとつの法平行化可能埋め込みから、いくつかの法フレーミング付き埋め込みを構成できます。Mが連結なら、ひとつの法平行化可能な超曲面埋め込みに対して2つの法フレーミング付き埋め込みがあります。

法平行化可能性と法フレーミング付き構造は、多様体ではなくて超曲面埋め込みの性質／構造です。にも関わらず、2次元多様体の超曲面埋め込み i:M→R3 のときは、超曲面埋め込みの法平行化可能性が“Mの向き付け可能”として、超曲面埋め込みの法フレーミングが“Mの向き”として語られます。これは合理化できるのでしょうか。

外積代数バンドルと法バンドル

多様体それ自身の向き（いわば内在的向き）の定義として、冒頭で言った外積代数バンドルを使った定義を採用しましょう（「多様体の向き：色々な定義」参照）。

i:M→X は超曲面埋め込み、dim(M) = m とします。多様体Mの向きも、超曲面埋め込み (M, i) の向きも、直線バンドルとそのセクションに関係しています。もし、2つの直線バンドル Λm(TM), N(M, i) が（ベクトルバンドルとして）同型なら、次が言えます。

  • Λm(TM) が平行化可能 ⇔ N(M, i) が平行化可能
  • Γ(Λm(TM)) \cong Γ(N(M, i))

言葉使いを変えるならば：

  • 多様体Mが向き付け可能 ⇔ 超曲面埋め込み (M, i) が向き付け可能
  • 多様体Mの向きの集合 \cong 超曲面埋め込み (M, i) の向きの集合

つまり、向き付け可能性／向きの議論において、「多様体M」と「超曲面埋め込み (M, i)」は置き換えてもいいことになります。

という事情で Λm(TM) \cong N(M, i) が欲しいのですが、Λm(TM)\oplusTM \cong i#TX が示せればOKです。なぜなら； ベクトルバンドルの線形代数から、Λm(TM)\oplusTM \cong i#TX ならば Λm(TM) \cong i#TX/TM ですが、右辺は N(M, i) に他なりません。

Λm(TM)\oplusTM \cong i#TX を示すには、定義に従ってベクトルバンドルの同型写像を構成することになるでしょうが（なんかアクロバットがあるのか？）、頑張れば出来そうです。このとき、Xは任意の多様体ではなくて、R3（一般化すればRn）なので、次のような良い性質が使えます。

  1. 向き付け可能である。より強く、接バンドルは平行化可能である*6。
  2. 標準的な向きが存在する。接バンドルに標準的なフレーミングがひとつ指定されている。
  3. 標準的なリーマン計量が存在する。

古典曲面論で、多様体の性質／構造を、超曲面埋め込みの性質／構造として語ることは合理化できるわけですが、異なる概念がいっしょくたになっているのは好ましくない気がします。

[補足]余談：
「0次元多様体の向きの定義が納得できない」において、TN(M) := TM\oplus_{\perp}LM （LMは自明な直線バンドル）というベクトルバンドルを出しましたが、Mが向き付け可能ならば、

  • TM\oplusΛm(TM) \cong TM\oplusLM \cong TM\oplusR

となります。Mの向き付け可能性に関係なく、新たに TN(M) を、

  • TN(M) := TM\oplusΛm(TM) = Λ1(TM)\oplusΛm(TM)

と定義すると、TN(M) は超曲面埋め込みの議論に使えそうです。
[/補足]

0次元多様体の向きに疑問を感じたのをキッカケに（「0次元多様体の向きの定義が納得できない」参照）、ちょっと向きについて考えたのですが、向きは思いのほか複雑な概念ですね。「よくわからん」と放り出したコホモロジー的向き（https://ncatlab.org/nlab/show/orientation+in+generalized+cohomology）も少しは理解したいな。

*1:ΓM(frame(E)) のセクションを、E→M×Rm という写像とみなす場合は大域自明化、逆方向の M×Rm→E という写像とみなす場合は大域フレーム場、と区別することがあります。

*2:埋め込みから単射性を除くとはめ込み〈immersion〉になります。埋め込みを単射はめ込み〈injective immersion〉と呼んだほうが、全射しずめ込み〈surjective submersion〉とペアになっていいと思うけど、埋め込みは多用されるから短く呼ぶのはしょうがない。

*3:この完全列から言えば、埋め込みの法バンドルは、埋め込みの微分が定める余核バンドル〈cokernel bundle〉 Coker(Di) です。

*4:ついでに、ということもありますし、いずれどこかで使うような気がするので。

*5:歴史をちゃんと調べる気はないので、僕の推測です。

*6:Mが平行化可能ならば、Mは向き付け可能であるのは明らかですが、逆は成立しません。その反例は2次元球面 S2 です。