多タプル・多行列とその計算 1/2

数を一方向に並べたタプル（数ベクトルともいう）と、数を二方向に並べた行列に対する計算手法が行列計算です。行列計算はスンバラシイと思います。どこがスンバラシイかというと； タプルや行列は、ベクトルや線形写像の表現になっていますが、そのことを知らなくても計算は機械的に出来ることです。実際、ベクトル空間・線形写像について（おそらく）何も知らない計算機が行列計算を実行しています。

しかし、双対ベクトル空間やベクトル空間のテンソル積が入ってくると、通常のタプル・行列ではうまく表現できません。そこで、タプル・行列を拡張した計算用データが登場します。それを通常“テンソル”と呼びます。ここでは、“テンソル”という言葉は避けて多タプル〈polytuple〉、多行列〈poolymatrix〉という言葉を使います*1。多タプル・多行列を使えば、双対とテンソル積を含む線形代数の対象物もうまく表現できて、機械的な計算が出来ます。

多タプル・多行列の計算は、いわゆる「テンソル計算」と内容的には同じですが、通常のタプル・行列をできるだけ素直に拡張することを目指します。伝統的だがヨクワカラン慣習や暗黙の前提は排除します。

2回に分けて記述する予定で、これは1回目の記事です。

内容：

タプルと行列の復習

タプル・行列の成分／係数は実数に限ります。以下、成分／係数には言及しません。圏論を本格的に使うわけではありませんが、圏の定義くらいは必要です。行列の全体が圏になっていることは使います。次の過去記事（14年前）を参照してください。

• はじめての圏論 その第1歩：しりとりの圏
• はじめての圏論 その第2歩：行列の圏

行列の圏をMatと書きます*2。Matの対象の集合はN（自然数全体の集合）で、ホムセット Mat(m, n) はm列n行（m行n列ではない）の行列の全体です。結合〈composition〉は、A;B = BA := BA （併置は行列の掛け算）で、恒等射は単位行列 id_n := I_n = (n列n行の単位行列) です。

（実数成分の）タプルは Rⁿ = R×...×R（n個のR） の要素として定義されるのが普通ですが、ここでは、タプルを関数〈写像〉として定義しましょう。

• Tup(n) := Map({1, ..., n}, R)

Tup(n)の要素が（長さnの）タプル〈tuple〉です。ここで、Map(A, B) は、集合Aから集合Bへの関数〈写像〉の全体です*3。

特に、

• Tup(1) := Map({1}, R) R
• Tup(0) := Map({}, R) 1 （1は単元集合）

x∈Tup(n) , i∈{1, ..., n} に対して、xは関数だったので関数値 x(i)∈R が一意的に確定します。この値をどう書くかは好みの問題です。次のような書き方があります。

1. x(i)
2. x[i]
3. x_i
4. xⁱ

ローカルになんかの約束をするのは勝手ですが、どう書こうと概念は同じです。書き方の違いは“書き方の違い”に過ぎません。くれぐれも見かけの違いに惑わされないように。

あらためて、行列もタプルと同様に関数として定義しておきます。

• Mat(m, n) := Map({1, ..., m}×{1, ..., n}, R)

たいていの人が、{1, ..., m}×{1, ..., n} にしようか {1, ..., n}×{1, ..., m} にしようか迷うでしょう。僕も迷いました。集合の直積 X×Y を使っても、Y×X を使ってもどっちでもいいときはよくあります。でも、どっちかを選ぶ必要があります。その選択は根拠なき選択になります。根拠なき〈必然性なき〉選択が現れたときは要注意です。「どっちでもいい」がゆえに、複数の方式がゴチャゴチャになる可能性があります（実際、たいていはゴチャゴチャになります）。

ゴチャゴチャの混乱を多少は緩和するために、(x, y)∈X×Y に対して、(y | x) := (x, y) という書き方を導入します。縦棒は、カンマとは逆順に成分を読むだけです。「マルコフ核： 確率計算のモダンな体系 // 書字順記法と反書字順記法」にも説明があります。

A∈Mat, (i, j)∈{1, ..., m}×{1, ..., n} に対して、関数値は A(​(i, j)) です。書き方のバリエーションは：

1. A(​(i, j))
2. A(​(j | i))
3. A[​(i, j)]
4. A[​(j | i)]
5. A_{(i, j)}
6. A_{(j | i)}
7. A^{(i, j)}
8. A^{(j | i)}

ペアの囲み括弧を省略すれば：

1. A(i, j)
2. A(j | i)
3. A[i, j]
4. A[j | i]
5. A_{i, j}
6. A_{j | i}
7. A^{i, j}
8. A^{j | i}

区切り記号であるカンマを省略した書き方は：

1. A(i j)
2. A[i j]
3. A_{i j}
4. A_ij （空白も省略）
5. A^{i j}
6. A^ij （空白も省略）

iとjを上下に振り分けることもあります。

1. A_i^j
2. A_jⁱ
3. Aⁱ_j
4. A^j_i
5. （上下が縦に揃っている）
6. （上下が縦に揃っている）

ローカルに約束を追加することはあるでしょうが、いずれにしても、無意味な“書き方の違い”は残ります。{1, ..., m}×{1, ..., n} か {1, ..., n}×{1, ..., m} かの選択と、書き方の選択の組み合わせは、けっこうな数になります。根拠なき選択と根拠なきローカルルールにより表記はゴチャゴチャになります。が、別に概念がゴチャゴチャになっているわけではありません。Tup(n) := Map({1, ..., n}, R), Mat(m, n) := Map({1, ..., m}×{1, ..., n}, R) と定義したので、この定義に基づき議論が進むだけです。書き方はどうでもいいです*4。

タプルと行列に関する幾つかの同型

行列圏のホムセットを Mat(m, n) と書きましたが、カンマの代わりに矢印で区切った Mat(m → n) でもいいとします。これからは、主に矢印区切りを使います。集合 {1, ..., n} が頻繁に登場するので、これを 〚n〛 と書くことにします。

• For n∈N, 〚n〛 := {k∈N | 1 ≦ k ≦ n}

[補足]以前は、〚n〛を [n] と書いていたのですが、角括弧〈ブラケット〉は他の目的でもよく使うので好ましくありませんでした。「ベクトル空間の基底とフレームは違う」では 1..n という記法を使いましたが、ちょっと長いですね。今回は二重角括弧にしてみます。二重角括弧もスコットブラケットとして意味論に登場しますが、記号のコンフリクトはどうせ避けられないので、まーいいとします。
[/補足]

Tup(n) の定義は、Tup(n) := Map(〚n〛, R) でした。さて、Tup(n) = Rⁿ でしょうか？ これは立場の問題です。Tup(n) = Rⁿ と Tup(n) ≠ Rⁿ のどちらが正しいか？ ではなくて、どちらの立場を取るか？ の問題です。我々は Tup(n) = Rⁿ を前提しないことにします。等式の成立は保証できませんが、次の同型は成立します。

• Tup(n) Rⁿ canonical

"canonical" は、単に同型（集合のあいだの全単射）が在るだけではなくて、規準的同型〈canonical isomorphism〉がひとつだけ在ることを意味します。規準的同型とは、皆さんがTHE・同型として想像する“その同型”です（これ以上の説明はしません）。

[補足]
ある程度形式化された集合論のなかで考えると、R×R = Map({1, 2}, R) ではないし、R×R Map({1, 2}, R) も自明ではないです。クラトフスキー〈Kazimierz Kuratowski〉による順序対の定義は (a, b) := {{a, b}, {a}} なので、R×R⊆Pow(Pow(R)) となります（Powはベキ集合）。一方、関数 f∈Map({1, 2}, R) は f⊆{1, 2}×R と考えるので、Map({1, 2}, R)⊆Pow({1, 2}×R) となり、これらの同型を与える関数は F⊆Pow(Pow(R))×Pow({1, 2}×R), G⊆Pow({1, 2}×R)×Pow(Pow(R)) となります。

直感的には明らかでも、規準的同型を与えるFとGを具体的に構成するのは、ちょっとめんどくさそうでしょ。
[/補足]

次の同型も規準的同型です。

• Mat(1 → n) Tup(n) canonical
• Mat(m → 1) Tup(m) canonical

規準的同型はあるが等しいとは言ってません。無理に、Mat(1 → n) = Tup(n) とか Mat(m → 1) = Tup(m) とか決めてもろくな事になりません。別な言い方をすると、次の問に無理に（何の根拠もなく）答えようとしてはいけません。

• タプルは縦ベクトル〈一列行列〉か、それとも横ベクトル〈一行行列〉か？

それに、「縦」「横」という形容詞も、我々がたまたま〈偶発的に〉採用した習慣に依存しているだけで何の必然性もありません。二種類を区別するラベルとして「縦」「横」を使っているだけです。

次の同型も重要ですが、これは規準的同型ではありません。

• Mat(m → n) Tup(m×n)

有限次元ベクトル空間と線形写像の圏はFdVectと書きます。頻繁に使う割に名前が長いし太字を使っているので、一文字'L'で略記します。

• L = FdVect

Tup(n) にも Mat(m → n) にも自然なベクトル空間構造が入るので、圏Lの対象と考えます。

• For m, n∈N, Tup(n), Mat(m → n) ∈|L|

Tup(n) は圏Lの対象（つまりベクトル空間）なので、ホムセット L(Tup(m), Tup(n)) を考えることができます -- これは、ベクトル空間 Tup(m) からベクトル空間 Tup(n) への線形写像の全体ですね。次の規準的同型があります。

• L(Tup(m), Tup(n)) Mat(m → n) canonical

Tup(n) Rⁿ canonical という規準的同型を組み合わせると：

• L(R^m, Rⁿ) Mat(m → n) canonical

規準的同型で結ばれている2つの集合は同一視可能です。が、同一視を何度も重ねるとワケワカラン状態になるので、過度の同一視はやめましょう。規準的同型が在るときでも、同一視するかの判断は慎重に。

ラムダ記法による関数の表現

「関数と関数値を区別しない」「引数変数や戻り値変数も込みで関数とみなす」は、古くからあり今でも使われている習慣ですが、ほんとにロクなもんじゃないです。早く絶滅して欲しいけど、あと100年くらいは使われそう。「関数と関数値を区別する」「引数変数や戻り値変数は関数の一部とはみなさない」ためには、関数をラムダ記法で表現するといいですね。

集合 X, Y と関数〈写像〉 f:X → Y があるとき、fは関数そのものですが、f(x) はYの要素です。当然ながら、f と f(x) は区別しなくてはいけません。f と f(x) の関係はラムダ記号'λ'を用いて次のように書けます。

• f = λx∈X.(f(x) ∈Y)

ラムダ記法／ラムダ計算をまったく知らないなら、以下の記事が入門になるでしょう。

• JavaScriptで学ぶ・プログラマのためのラムダ計算
• JavaScriptで学ぶ・プログラマのためのラムダ計算 問題集
• 絵を描いて学ぶ・プログラマのためのラムダ計算

関数fの余域〈終域〉が周知なら、λx∈X.(f(x)) でもかまいません。fの域〈始域〉も了解されているなら λx.(f(x)) と書くのも許します。が、ラムダ部〈ラムダ抽象部 | ラムダ束縛部〉である'λx.'は省略できません。

x∈Tup(n) ならば、xは関数なので、次のように書けます。

• x = λi∈〚n〛.(x(i) ∈R)

型（域・余域の集合）を省略するなら λi∈〚n〛.(x(i)) または λi.(x(i)) でもいいですが、x(i) だけでは関数ではなくて単なる実数値です。関数値を x_i, xⁱ と書くときは、ラムダ部を次のように書いてもいいとしましょう。ラムダ部がハッキリわかるように赤色ボールドにします。

• λi∈〚n〛.(x_i) を (x_i)_i∈〚n〛 と書いてもよい。
• λi.(x_i) を (x_i)_i と書いてもよい。
• λi∈〚n〛.(xⁱ) を (xⁱ)^i∈〚n〛 と書いてもよい。
• λi.(xⁱ) を (xⁱ)ⁱ と書いてもよい。

つまり、

• x = (x_i)_i∈〚n〛 = (x_i)_i
• x = (xⁱ)^i∈〚n〛 x = (xⁱ)ⁱ

簡略化されたラムダ部がない限り、タプル（＝関数）ではなくて実数値です。

「引数変数や戻り値変数は関数の一部とはみなさない」ので、引数変数〈ラムダ変数〉の名前はなんでもかまいません。

• x = (x_i)_i = (x_k)_k = (x_a)_a

引数が「添字」とか「インデックス」とか呼ばれる状況でも、それは「言葉と書き方だけの違い」であり、概念としては通常の関数として扱おうということです。関数値と関数の（意図的）混同はホントにやめようね。

極性付き自然数

Tup(n), Mat(m → n) に出現しているmやnは単一の自然数データでした。我々の目的からは、この「単一の自然数データ」を一般化する必要があります。どう一般化するかというと：

1. 単一のデータから、データの並びであるリストに一般化する。
2. 自然数から、極性付き自然数に一般化する。

一番目の“リスト化”は見当が付くでしょうが、“極性付き自然数”は意味不明ですね。極性付き自然数の説明をします。

P = {+, -} と置いて、二元集合Pの要素を極性〈polarity〉と呼びます。極性は、通常は符号〈sign〉と呼ぶものですが、符号と呼ぶと誤解と混乱をまねくので「極性」を使います。2つの極性はそれぞれ正〈positive〉の極性、負〈negative〉の極性ですが、「正負」で誤解をまねきそうなときは、'+'をアップ極性〈up polarity〉、'-'をダウン極性〈down polarity〉とも呼びます。

[補足]「符号」「正負」といった言葉が誤解をまねく危険があるのなら、そもそも'+'と'-'という記号をやめればいいのではないか？ -- ごもっともです。が、ペアになる記号で容易に読み書きできる記号が'+', '-'くらいしか見当たらないのですよね。
[/補足]

極性は、ベクトル空間の双対ペアの役割を識別する目的で使います。が、それは多タプル・多行列の“意味”を考える場合で、単なる機械的計算のときは「何だか知らんが2つの記号」として扱っても計算は進みます。

NP := N×P = N×{+, -} と定義して、NPの要素を極性付き自然数〈natural number with polarity | polarized natural number〉と呼びます。(n, +)∈NP を n+、(n, -)∈NP を n- と略記します。「極性付き自然数 n+, n-」は「整数 n, -n」とは別物だと思ってください。とはいえ、実を言うと僕はNPではなくて整数の集合Zを使っていました。Zを使っても理論的な問題はないのですが、よく知られたZゆえに余計な連想をされては困るので、ZではないNPを導入したのです。

写像 abs:NP → N, pol:NP → P を次のように定義します。

• abs(n+) = n
• abs(n-) = n
• pol(n+) = +
• pol(n-) = -

abs, pol は、直積である NP = N×P の直積因子への射影です。'abs'は絶対値〈absolute value〉のつもりで、極性を除いた自然数です。

写像 anti:NP → NP を次のように定義します。

• anti(n+) = n-
• anti(n-) = n+

antiで極性が反転します。antiを対蹠〈たいしょ | たいせき〉写像〈antipodal map〉と呼びます。対蹠写像antiは前置演算子記号'￢'でも表します。

• For μ∈NP, ￢μ := anti(μ)

記号'￢'は、論理の否定を表す記号ですが、￢￢μ = μ が“二重否定の法則”の形をしているので選びました。域・余域がNPの部分集合に制限された対蹠写像も、同じ記号'￢'で表します。

NPのなかで 0+ と 0- を同一視してできる集合を NP₀ とします（NP₀はZとソックリです）。同様に、0+ と 0- 、1+ と 1- を同一視してできる集合を NP₁ とします。NP → NP₀ → NP₁ という自然な全射があります。実際上は、NP₁ が一番使うと思います。1+ と 1- を同一視することは、Rの双対空間はR自身だとみなすことに相当します。

極性付き自然数のリストと多インデックスセット

極性付き自然数を（しばらくのあいだは） μ, ν などのギリシャ文字小文字で表します。極性付き自然数のリストは μ, ν などの下線付きで表すことにします。リストμの長さがrだとすれば：

• μ = (μ₁, ..., μ_r)

μ も、関数〈写像〉 μ∈Map(〚r〛, NP) だと思ってもかまいません。下線を付けるのは分かりやすさのためで、μ = (μ_a)_a∈〚r〛 と下線なしで書いても何の問題もありません。

[補足]タプルとリストは違うのでしょうか？ 単一のデータを見てもタプルとリストの区別は付きません。タプルかリストかは、データそのものを分類しているのではなくて、そのデータが所属する構造の違いを示唆しているのです。

プログラミングの常識的解釈では、タプルは固定長でリストは可変長だとされます。これは、タプルの集合では「データの長さは一定」とする習慣を反映しています。Xの要素を項目〈成分〉として長さがnのタプルの集合を Tup(n, X)、Xの要素を項目〈成分〉として長さが色々（可変）なリストの集合を List(X) としましょう。次の関係があります。（以下の'+'は集合の直和。）

• List(X) = Tup(0, X) + Tup(1, X) + Tup(2, X) + ...

List(X) には長さが異なるデータが混じっており、（特定のnに対する）Tup(n, X) に所属するデータは長さが一定です。

似た話で、とある集合Xに所属する要素xが「ベクトルかどうか」を考えてみましょう。集合Xや要素xをいくら眺めても答は出てきません。集合X上に線形構造（足し算とスカラー倍）が載っていれば「xはベクトルだ」と言っていいだろうし、そうでないときは「xはベクトルだ」とは（あまり）言いません。
[/補足]

一般に、集合Xの要素を並べたリストの全体を List(X) と書くので、極性付き自然数のリストの集合は List(NP) です。空リストはεと書きます。空リストを記号'ε'で書くのは一般的ですが、下線付きにしたのは成り行き上です。(3-, 2-, 2+), (3-), (3+, 5+), () などは List(NP) の要素の例です。

μ∈List(NP) に対して、集合〚μ〛を定義しましょう。

• μ∈NP, μ = m+ のとき、〚μ〛 := {1+, ..., m+}
• μ∈NP, μ = m- のとき、〚μ〛 := {1-, ..., m-}
• μ∈List(NP), μ = (μ₁, ..., μ_r) のとき、〚μ〛 = 〚(μ₁, ..., μ_r)〛 := 〚μ₁〛×...×〚μ_r〛
• 特に、〚(μ)〛 = 〚μ〛
• 特に、〚ε〛 = 〚()〛 = 1 = (特定された単元集合)

特定された単元集合は何でもいいのですが、何かに決まってないと不安な人のために 1 = {1} と約束しておきます。ホントに何でもいいのですが。

具体例として、〚(3-, 2-, 2+)〛を求めてみましょう。定義より、〚(3-, 2-, 2+)〛 = 〚3-〛×〚2-〛×〚2+〛 = {1-, 2-, 3-}×{1-, 2-}×{1+, 2+} です。この集合は12個の要素を持つので全部列挙すると：

1. (1-, 1-, 1+)
2. (1-, 1-, 2+)
3. (1-, 2-, 1+)
4. (1-, 2-, 2+)
5. (2-, 1-, 1+)
6. (2-, 1-, 2+)
7. (2-, 2-, 1+)
8. (2-, 2-, 2+)
9. (3-, 1-, 1+)
10. (3-, 1-, 2+)
11. (3-, 2-, 1+)
12. (3-, 2-, 2+)

集合 〚μ〛 = 〚(μ₁, ..., μ_r)〛 の要素の個数は abs(μ₁)×...×abs(μ_r) になります。今の例では、〚(3-, 2-, 2+)〛 の個数は abs(3-)×abs(2-)×abs(2+) = 3×2×2 = 12 でした。

我々は、タプルも行列も関数だと定義しました。同様に、多タプルと多行列も関数として（後で）定義します。そのとき、関数の引数〈argument〉として極性付き自然数のリストを使うのです。関数〈写像〉の「引数」「入力値」を「インデックス」とも呼ぶので、“関数である多タプル・多行列”への引数を多インデックス〈polyindex〉と呼びます。多インデックスの集合が多インデックスセット〈set of {polyindexes | polyindices}〉で、“関数である多タプル・多行列”の域〈始域〉となる集合です。

関数〈写像〉の「引数」、「入力値」、「インデックス」は同義語です。ニュアンスはありますが、ニュアンスは心理的なもので形式的定義には影響しません。「極性付き自然数のリスト」と「多インデックス」はモノとしては同じモノです。「多インデックス」は、特定の使用目的を想定しての呼び名です -- 多タプル・多行列への引数として使用することを想定しています。

多インデックスセットを順序により記述する

多インデックスセットは重要なので、もう少し調べましょう。極性付き自然数のリストの集合 List(NP) の勝手な部分集合が多インデックスセット（多タプル・多行列への引数の集合）になれるわけではありません。非常に特殊な“形”の部分集合だけを多インデックスセットと呼んでいます。その“形”を、順序に基づく区間〈interval〉あるいは矩形〈rectangle〉として記述しましょう。

これから扱う極性付き自然数の集合はNP₀とします。NP₀内では、0+ = 0- が成立します。0 := 0+ = 0- と置きましょう。0は、NP₀上の対蹠写像の唯一の不動点です。つまり、￢0 = 0 。NP₀は、集合としてはZと区別が付きませんが、Zとは異なる順序を入れます。次の図で、線で繋がれていて上にある要素のほうが“大きい”とします。この順序は全順序にはなりません。

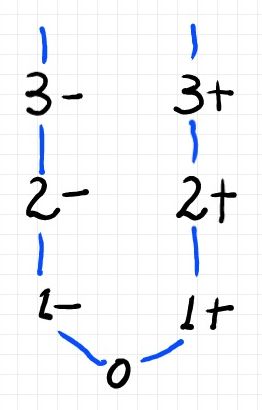
NP₀のこの順序構造を頭に焼き付けてください。

NP₀内で、μ以下の極性付き自然数達（ただし0は除く）は区間の形になります。この区間が〚μ〛です。

• For μ∈NP₀, 〚μ〛 := {a∈NP₀ | 0＜ a ≦μ}

集合の定義のなかでラテン文字'a'を使いました、aも極性付き自然数を表す変数です。区間の特別なものとして：

• 〚0〛 = {}
• 〚1+〛 = {1+}
• 〚1-〛 = {1-}

μとνを同じ長さ（長さ＝r）の極性付き自然数のリストだとして、μ＜ν、μ≦ν を次のように定義します。

• μ＜ν :⇔ ∀i∈〚r〛.(μ_i＜ν_i)
• μ≦ν :⇔ ∀i∈〚r〛.(μ_i≦ν_i)

注意すべきは、μ＜ν ⇔ (μ≦ν かつ μ≠ν) は成立しないことです。μ＜ν やμ≦ν と書くときは、μとνの長さは等しいと暗黙に仮定します。異なる長さのリストのあいだの順序は考えません。

[補足]「異なる長さのリストのあいだの順序は考えません」は、「順序を考えない順序」を考えているかも知れません。関係記号'≦'に相当するブール値の関数を le:List(NP₀)×List(NP₀) → {true, false} とします。2つのリストμとνの長さは違うとします。le(μ, ν) の値をどう決めるか？ 2つの選択肢があります。

• le(μ, ν) = false と決める。（leは全域述語になる。）
• le(μ, ν) は未定義とする。ソフトウェア的に言えば例外を投げる。（leは部分述語になる。）

今の文脈では、どちらにしてもかまいません。
[/補足]

極性付き自然数のリストのあいだの順序を使うと、多インデックスセットは次のように定義できます。

• For μ∈(NP₀)^r, 〚μ〛 := {a∈(NP₀)^r | 0＜ a ≦μ}

集合の定義のなかの下線付きラテン文字'a'は極性付き自然数のリストを表す変数です。0は、0が並ぶリストを表しています。

μ∈(NP₀)^r に対する集合〚μ〛は、矩形の形をしています。区間〚μ〛が最大値μで一意的に決まったのと同様に、矩形〚μ〛も最大値μで一意的に決まります。次のような言い方ができます。

• 多インデックスセット〚μ〛は、“μ以下の”多インデックス（ただし、成分として0を含まない）からなる集合である。

多インデックスの書き方

多インデックスと多インデックスセットに親しめば、多タプル・多行列の理解は容易です。多タプル・多行列の計算は、“添字の計算術”としての伝統的テンソル計算を含みます。しかし、伝統的（むしろ因習的）テンソル計算を学んだ人は「極性付き自然数も多インデックスも見たことないぞ」と言うでしょう。それは、極性付き自然数や多インデックス（極性付き自然数のリスト）が表に出ないような記法を採用しているからです*5。その記法を紹介しますが、伝統的テンソル計算に興味がない人はこの節を完全に飛ばしても大丈夫です。

具体例として、多インデックスセット〚(2-, 3+, 3-)〛に所属する多インデックス、例えば (2-, 1+, 2-) について考えましょう。(2-, 1+, 2-)≦(2-, 3+, 3-) かつ (0, 0, 0)＜(2-, 1+, 2-) なので、確かに (2-, 1+, 2-)∈〚(2-, 3+, 3-)〛 です。伝統的テンソル計算では、次のルールで極性を明示的に書くのを避けます。

• 極性がアップ（'+'）である極性付き自然数は、 '' のように上付きで表記する。
• 極性がダウン（'-'）である極性付き自然数は、 '' のように下付きで表記する。

このルールを採用すると：

• 

さらに区切り記号のカンマを省略します。

• 

多インデックスセット〚(2-, 3+, 3-)〛 からの関数 x:〚(2-, 3+, 3-)〛 → R があると、xに対して引数 (2-, 1+, 2-) を渡した形は次のように書けます。

囲み記号の括弧や引数渡しの括弧も省略してしまうわけです。

さらに、リストの項目〈成分〉を“ある程度は”置換で入れ替えてもいいとします（微妙すぎてよく分からないルール*6）。例えば、

• 

このよく分からないルールを使い、さらに上下の位置を揃えた（空白を詰めた）レイアウトに変形してもいいとして：

ちなみに、下付きの'22'は二十二ではなくて (2, 2) のカンマが省略されたと考えます（「テンソル計算：112はイチイチニかヒャクジュウニか」参照）。

は、 に比べるとはるかにコンパクトです。しかし、コンパクトさの代償に色々とワケワカラナイことを（暗黙に）持ち込んでしまっています。「上下添字の技〈わざ〉を使いこなせば便利」なことは認めます*7。しかし、その技〈わざ〉が使えないと何かが出来ないわけではありません。因習的な技を代替する、もっとクリアでモダンな手法があります。と、そんな理由で、我々は極性を明示的に添えた極性付き自然数のリスト（多インデックス）を省略記法なしでそのまま使います。

多インデックスセット上の対蹠写像

これから関数名や演算子記号をオーバーロード〈多義的使用〉するので、オーバーロード解決用の記法を導入しておきます。f:X → Y が写像で、A⊆X のとき、fをA上に制限した写像を f|_A:A → Y と書きます。f と f|_A をオーバーロードする（同じ名前・記号で表す）ことはよくあります。f:X → Y が単射のとき、fの像 Im(f)⊆Y でだけ定義された逆写像が作れます。Im(f)上でだけ定義されたfの逆写像〈部分逆写像〉を f^～1:Im(f) → X と書きます。f^～1 がfのホントの逆写像とは限りません。f と f^～1 もオーバーロードされることがあります。

さて、既に定義した対蹠写像 anti:NP₀ → NP₀ を、Anti:List(NP₀) → List(NP₀) へと拡張します。Antiは次のように定義します。

• Anti(ε) := ε （長さ0のリストのとき）
• Anti(​(μ)) := (anti(μ)) （長さ1のリストのとき）
• Anti(​(μ₁, μ₂)) := (anti(μ₂), anti(μ₁)) （長さ2のリストのとき）
• Anti(​(μ₁, μ₂, ..., μ_r)) := (anti(μ_r), anti(μ_r-1), ..., anti(μ₁)) （長さrのリストのとき）
• 例： Anti(​(2-, 1+, 5-, 1-)) = (1+, 5+, 1-, 2+)

各成分の対蹠〈antipode〉を取るだけではなくて、リストの並び順が反転〈reverse〉することに注意してください。

anti^-1 = anti でしたが、同様に Anti^-1 = Anti です。空リストεと単元リスト（長さ1のリスト）(0) が写像Antiの不動点です。そして、次の図式が可換になります。図式内のsingleは要素から長さ1のリストを作る写像です。

antiもAntiも前置演算子記号'￢'で表現します。また、AntiをList(NP₀)の部分集合に制限した写像も同じくAntiまたは'￢'と書きます。これは、かなり紛らわしくなります。μ∈List(NP₀) として、Antiを 〚μ〛⊆List(NP₀) に制限すると：

• Anti|_〚μ〛:〚μ〛 → List(NP₀)

これは単射なので部分的逆が作れます。

• (Anti|_〚μ〛)^～1:Im(Anti|_〚μ〛) → 〚μ〛

Im(Anti|_〚μ〛) = 〚anti(μ)〛 が成立するので、

• (Anti|_〚μ〛)^～1:〚Anti(μ)〛 → 〚μ〛

(Anti|_〚μ〛)^～1は可逆なので、

• (​(Anti|_〚μ〛)^～1)^-1:〚μ〛 → 〚Anti(μ)〛

今まで出てきた anti, Anti, (Anti|_〚μ〛)^～1, (​(Anti|_〚μ〛)^～1)^-1 はすべて前置演算子記号'￢'で書かれます。次のように：

1. ￢ε := ε
2. ￢(μ) := (￢μ)
3. ￢(μ₁, μ₂) := (￢μ₂, ￢μ₁)
4. ￢(μ₁, μ₂, ..., μ_r) := (￢μ_r, ￢μ_r-1, ..., ￢μ₁)
5. ￢〚μ〛 = 〚￢μ〛 （左辺は写像￢の像集合）
6. ￢：〚μ〛 → 〚￢μ〛
7. ￢：〚￢μ〛 → 〚μ〛

オーバーロードされた'￢'のそれぞれの意味と使い方をよーく確認してください。次の可換図式が理解の助けになるかも知れません -- 上の箇条書き5番の内容です。図式内で、Rectは μ 〚μ〛 という写像で、Powはベキ集合関手です。

μ∈List(NP₀) に対する Rect(μ) = 〚μ〛の形の集合（ベキ集合 Pow(List(NP₀)) の要素）が多インデックスセットです。多インデックスセットを Pow(Anti):Pow(List(NP₀)) → Pow(List(NP₀)) で移しても多インデックスセットです。

'￢'のオーバーロードが紛らわし過ぎるときは、τ_μ:〚μ〛 → 〚￢μ〛 と (τ_μ)^-1 = τ_￢μ:〚￢μ〛 → 〚μ〛 という記号も使います。'τ'〈タウ〉は（極性の）トグルにちなみます。

対蹠写像はややこしいですが、ベクトル空間の双対ペアの挙動を機械的計算に取り込むには必要なメカニズムです。

多タプルと多行列の定義

極性付き自然数、多インデックス（極性付き自然数のリスト）、多インデックスセット（区間／矩形の形をした多インデックスの集合）について詳しく説明しました。それというのも、多インデックスセットは多タプル・多行列を定義する素材だからです。多インデックスセットがあれば、多タプルと多行列の定義は難しくはありません。

• For μ∈List(NP₀), PTup(μ) := Map(〚μ〛, R)
• For μ, ν∈List(NP₀), PMat(μ → ν) := Map(〚μ〛×〚ν〛, R)

集合 PTup(μ) の要素をタイプμの多タプル〈polytuple of type μ〉、集合 PMat(μ → ν) の要素をプロファイル μ → ν の多行列〈polymatrix of profile μ → ν〉と呼びます。

多タプルと多行列は、通常のタプル・行列に比べて、タイプ／プロファイルに極性が付いてリスト化されています。この一般化はかなり素直な一般化で、通常のタプル・行列が持つ性質は多タプル・多行列にも継承されています。

• PTup(μ) も PMat(μ → ν) もベクトル空間とみなせる。
• PTup(μ), PMat(μ → ν) のベクトル空間としての次元は、タイプμ、プロファイル μ → ν から計算できる。
• 多インデックスセット〚μ〛は、ベクトル空間としてのPTup(μ)の基底集合とみなせる。（自然な埋め込みの像が基底集合。）
• 多インデックスセットの直積〚μ〛×〚ν〛は、ベクトル空間としてのPMat(μ → ν)の基底集合とみなせる。（自然な埋め込みの像が基底集合。）
• PMat(ε → ν) PTup(ν) canonical
• PMat(μ → ε) PTup(μ) canonical
• For μ, ν∈List(NP₀), L(PTup(μ), PTup(ν)) PMat(μ → ν) canonical

さらに、多インデックスの対蹠や、2つの多インデックスの連接〈concatenation〉を利用してより豊かな構造を定義できます。それらの構造と、多タプル・多行列の計算法は次の記事（2/2）とします。

*1:「テンソル」という言葉があまりに多義的に使われていて、コミュニケーションが困難になるからです。

*2:Matが太字じゃない理由（とも言えない気分）は「ベクトル空間の基底とフレームは違う // 補足」に書いてあります。

*3:Map(A, B) = Set(A, B) ですが、集合圏を表に出す必要がないときはMapを使います。

*4:そうは言っても、世間で使われている代表的な書き方は紹介します。

*5:極性付き自然数を使う方法と比較するとそう見える、ということです。伝統的テンソル計算の記法成立の歴史的経緯は、極性付き自然数とは何の関係もないでしょう。

*6:ホントは分かります。アップ極性とダウン極性の項目が混じったリストに対して、アップ極性が先（左側）に来るように項目の入れ替えをします。

*7:例えば「なぜにテンソル記法は意味不明なのか」では、「実際、テンソル記法における、上下添字の書き分けや総和記号の省略（アインシュタインの規約）はホントに素晴らしいアイディアです。これは魅力的ですね。」と書いています。