3次元ユークリッド空間と余接バンドルのメタファー - 檜山正幸のキマイラ飼育記 (はてなBlog)

我々が住んでいるこの空間は、常識的・直感的に3次元ユークリッド空間だとみなしていいでしょう。3次元ユークリッド空間を、多様体の言葉で表現するとどうなるでしょうか。3次元ユークリッド空間の多様体風定義の後で、余接バンドルに対するある種のメタファーについて述べます。

注：この記事内に出てくる '?' や '|' の意味はその場で説明してますが、詳しくは「用語のバリエーション記述のための正規表現」参照。

内容：

3次元アフィン空間
3次元アフィン空間の接バンドル
接バンドルの内積：3次元ユークリッド空間の定義
3次元ユークリッド空間の余接バンドル／余接ベクトル

3次元アフィン空間

3次元ユークリッド空間は3次元アフィン空間に長さや角度の概念が入ったものです。アフィン空間については次の記事で説明しています。

単一のアフィン空間を考えるだけなので圏云々は無視してかまいません。上記一番目の過去記事では、（一般的）アフィン空間を (A, V, d) と書いてますが、THE・3次元アフィン空間は (E, V, d) と書くことにします。'E' は Euclid から。もちろん、ベクトル空間Vの次元は3です。

d:E×E → V は“点と点のあいだの引き算”です。上記一番目の過去記事では、dを引き算記号 '-' で、dの（だいたい）逆である作用 E×V → E を足し算記号 '+' で表してますが、ベクトル空間Vの引き算・足し算と混同されるのが嫌なので、ここでは、引き算 y - x の代わりに y←x、足し算 x + v の代わりに x▷v とします。

Eは点の空間です。x∈E は点です。
Vはベクトルの空間です。v∈V はベクトルです。
2つの点 x, y に対して、y←x は、xからyへと向かう{平行}?移動ベクトルです（「{…}?」は、「…」が省略可能であることを意味します）。あるいは、xを基点としたyの位置ベクトルです。

点の空間Eから、順序付きの4点 a, b, c, d （この順序）を選びます。3つのベクトル b←a, c←a, d←a がVで一次独立なとき、(a, b, c, d) を{アフィン枠 | アフィンフレーム}と呼びます（「{… | …}」は縦棒の左右どちらでもよいことを意味します）。アフィンフレームの最初の点を（選択された）原点と呼びます。アフィンフレーム (a, b, c, d) を、v₁ := b←a, v₂ := c←a, v₃ := d←a と置いて (a; v₁, v₂, v₃) のように書くこともあります。

アフィンフレーム (a; v₁, v₂, v₃) があると、次の写像を作れます。

${\bf R}^3 \ni (\xi_1, \xi_2, \xi_3) \mapsto a\triangleright (\xi_1 v_1 + \xi_1 v_2 + \xi_3 v_3) \in E$

この写像のことも{アフィン枠 | アフィンフレーム}と呼びます。写像としてのアフィンフレーム R³ → E は可逆なので、逆写像があります。

$E \ni x \mapsto (\xi_1, \xi_2, \xi_3) \in {\bf R}^3$

逆写像 E → R³ のほうは（アフィン空間の）アフィン座標です。順序付きの4点であるアフィンフレームを選べば、アフィン座標が一意的に決まります。

3次元アフィン空間の接バンドル

アフィン座標を、単一のチャート＝局所座標（実は大域座標だが）を持つアトラスと考えれば、点の空間Eは3次元多様体になります。多様体としてのE上の接ベクトルは、平行移動ベクトル〈位置ベクトル〉と同一視可能です。つまり、

TE $\cong$ E×V

この同型はベクトルバンドルとしての同型でもあり、次の図式は可換です。

$\require{AMScd} \begin{CD} TE @>{\cong}>> E\times V \\ @V{\pi}VV @VV{\pi_1}V \\ E @= E \end{CD}$

ここでは、同型を“同じ”とみなしてしまいましょう。

TE = E×V

アフィンフレーム／アフィン座標は、E $\cong$ R³ の同型を与えますが、同時に V $\cong$ R³ の同型も与えます。これらの同型により、次の同型が得られます。

TE = E×V $\cong$ R³×R³

TE → R³×R³ の向きの同型射が、接バンドルの全空間の座標（単一の局所座標＝大域座標）になります。このとき、点の座標とベクトルの座標〈成分〉がゴッチャになりやすいので、次の記法を使うことにします。

$E\ni x \longleftrightarrow (\xi_1, \xi_2, \xi_3) \in ({\bf R}^3 \mbox{ as point})\\ V\ni v \longleftrightarrow \begin{bmatrix} \eta^1 \\ \eta^2 \\ \eta^3 \end{bmatrix} \in ({\bf R}^3 \mbox{ as vector}) \\ TE\ni (x, v) \longleftrightarrow \begin{bmatrix} \eta^1 \\ \eta^2 \\ \eta^3 \end{bmatrix}\!\!@(\xi_1, \xi_2, \xi_3) \in ( {\bf R}^3\times {\bf R}^3 \mbox{ as point-vector pair})\\$

η@ξ は「座標がξである点から出ている、成分がηである接ベクトル」の表示です。ηのインデックスが上付きなのは微分幾何の習慣に合わせました。

座標・成分の足し算は、幾何的には2つのケースがあって、同一点上の2本のベクトルの足し算と、点とベクトルの足し算（平行移動）があります。

$\mbox{For } v, v' \in T_x E \\ v + v' \longleftrightarrow \begin{bmatrix} \eta^1 + \eta'^1 \\ \eta^2 + \eta'^2 \\ \eta^3 + \eta'^3 \end{bmatrix}\!\!@(\xi_1, \xi_2, \xi_3) \: \\ \: \\ \: \\ \mbox{For } x\in E, v \in T_x E \\ x + v = x\triangleright v \longleftrightarrow (\xi_1 + \eta^1, \xi_2 + \eta^2, \xi_3 + \eta^3)$

接バンドルの内積：3次元ユークリッド空間の定義

3次元ユークリッド空間には長さや角度の概念があります。これは、接バンドルTEに内積が入っていることで表現できます。TEの内積をgとします（文字 'g' の使用も微分幾何の習慣から）。

gの実体は次の可換図式を満たす写像です。

$\begin{CD} TE\times_E TE @>{g}>> E\times {\bf R} \\ @V{\pi}VV @VV{\pi_1}V \\ E @= E \end{CD}$

この可換図式が成立するなら、gを g:TE ×_E TE → R だと思ってもかまいません。TE ×_E TE はベクトルバンドルのファイバー積ですが、TE = E×V と同一視していたので、ファイバー積は次のように書けます。

$TE\times_E TE := \{( (x, v), (y, w))\in TE\times TE\mid x = y\} \cong E\times(V\times V)$

T_xE のベクトルを（念のため） v@x のように書くこととして、g(v@x, w@x) はスカラー値になります。x ≠ y のときの g(v@x, w@y) は無意味（未定義）です。

g(v@x, w@x) を g_x(v, w) とも書くことにします。xを固定したときに、g_x(v, w) は通常の意味でのVの内積です。xを動かすと、g_x も動く可能性がありますが、これが動くと厄介なので、g_x はxに依存しないとします。そうすれば、次の等式が、x, y が何であっても成立します。

g(v@x, w@x) = g(v@y w@y) あるいは g_x(v, w) = g_y(v, w)

内積gの表示が簡単になるようにEのアフィンフレームを選びましょう。アフィンフレーム (a; v₁, v₂, v₃) を、次の等式が成立するように選びます。

$g_a(v_i, v_j) = \delta_{i\,j}$

右辺はクロネッカーのデルタです。この等式が成立するようなアフィンフレームを正規直交{アフィン}?フレームと呼びます。正規直交フレームから誘導されるアフィン座標を使えば、内積の表示は簡単になります。

$\mbox{For } v@x, v'@x \in T_x E \\ g(v@x, v'@x) = g_x(v, v') \longleftrightarrow (\eta^1 \eta'^1 + \eta^2 \eta'^2 + \eta^3 \eta'^3)@(\xi_1, \xi_2, \xi_3)$

内積の結果を「スカラー@点」の形で書いてますが、スカラーは点によらないので普通はスカラーが載っている点は無視します。この無視は、自明バンドル π₁:E×R → E を単なるRとみなすことに対応します。

接{ベクトル}?バンドルに今説明したような内積が入った3次元アフィン空間が3次元ユークリッド空間です。3次元ユークリッド空間のアフィンフレームとしては正規直交フレームを取ることが多いです（そうでないと不便なので）。

3次元ユークリッド空間の余接バンドル／余接ベクトル

前節までで、3次元ユークリッド空間の多様体風の定義は終わりです。用語法を注意しておくと、位置ベクトル、{平行}?移動ベクトル、接ベクトル、速度ベクトル、反変ベクトル などの言葉は、TE = E×V または V の要素を指すために割とテキトーに使われます。特に、フレームを固定して座標表示／成分表示すると、点、特定点上の接ベクトル（束縛ベクトル）、自由ベクトル（特定の点と紐付いてないVの要素、自由ベクトル空間とは無関係）がすべてスカラー3つ組で表示されるので、なおさらテキトーになります。

多様体においては、接バンドルと共に余接バンドルも考えます。3次元ユークリッド空間でも余接バンドルとその要素である余接ベクトルを考えることはあるのですが、内積があるので、ほとんど場合は接バンドル／接ベクトルで代用できます。「余接バンドル／余接ベクトルなんて要らない」と言えるでしょう。

しかし、しかしですね、「接ベクトルとは違ったナニカとしての余接ベクトル」を考えることもあるっちゃあります。例えば、E上の関数を微分した勾配ベクトル場は、接ベクトル場（点への接ベクトルの割り当て）ですが、微分が局所的な1次関数近似なので、「接ベクトルで表現される1次関数」の場という雰囲気になります。これを多様体の標準的言葉で言うなら“1次微分形式＝余接ベクトル場”です。接ベクトルで表現される{斉次}?1次関数とは、Vの標準双対ベクトル空間V^*の要素そのものです。

w∈V に対して f:V → R を、f(v) := g(w, v) と定義しましょう。内積gは点に関係しないので、g_x のような書き方はやめて単に g:V×V → R にしました。今定義した f∈V^* が接ベクトル w で表現される{斉次}1次関数ですが、これを「接ベクトル w とは違ったナニカ」として理解しましょう。ここでの「理解」は、感覚的なメンタルモデルを得ることです。

{線形 | {斉次}?1次}{関数 | 形式} f:V → R はゼロではないとします。すると、Ker(f) = {v∈V | f(v) = 0} ⊆ V が平面（2次元部分ベクトル空間）として決まります。この平面が、 f を表示する幾何的実体になります。ただし、異なる線形関数が同じ平面を規定することがあります。そこで、もう一枚の平面 {v∈V | f(v) = 1} も考えます。2枚の平面を仮にレベル0平面（Kef(f) のこと）、レベル1平面と呼びましょう。次のことが分かります。

レベル0平面とレベル1平面は平行。
線形関数 f は、レベル0平面上で値0となる。
線形関数 f の値は、レベル0平面からレベル1平面の方向に増加する。
レベル0平面とレベル1平面の間隔が狭いほど、線形関数 f の増加の度合いは大きい。

レベル0、レベル1だけではなくて、‥‥ レベル(-2ε)平面、レベル(-ε)平面、レベル0平面、レベルε平面、レベル2ε平面、‥‥ を考えると、3次元ベクトル空間Vは、層状に平行な平面達で埋め尽くされます。この「層状に平行な平面達」は線形関数 f の表現として十分なものです。

層状に平行な平面達を垂直に貫く直線（Vの1次元部分ベクトル空間）を考えましょう。この直線は先の平面達への法線です。のっぺらぼうな直線ではなくて、平面達との交点に ‥‥ -2ε、-ε、0、ε、2ε、‥‥ の目盛りが刻んであるとします。この目盛り付き法線もまた線形関数 f の表現として十分なものです。

そういう事情で、次の言い方で、線形関数 f を指し示すことがあります。

平面{の{束 | 層}}
法線（ただし、目盛り付き）

事実としては、「平面」はもとの接ベクトル w に直交する2次元部分ベクトル空間だし、「法線」はもとの接ベクトル w が生成する1次元部分ベクトル空間です。が、言葉を変えることによって、余接バンドル側の対象物を参照しています。内積によって重なってしまった2つの実体を分離する方便として「平面」「法線」が使われています。

「平面」「法線」はとてもインフォーマルで誤解をまねく言葉ですが、フォーマルな同義語に次があります。

{線形 | {斉次}?1次}{関数 | 形式}
{余接 | コ}ベクトル
共変ベクトル
双対ベクトル

f∈V^* ではなくて f∈T^*E と考えるときは、f@x∈T^*_xE と書いて、その成分表示は横ベクトルにするのがいいでしょう。

$\mbox{For } f@x \in T_x^\ast E \\ f@x \longleftrightarrow \begin{bmatrix} \omega_1 & \omega_2 & \omega_3 \end{bmatrix}\!\!@(\xi_1, \xi_2, \xi_3)$

f@x の成分表示 [ω₁ ω₂ ω₃]@(ξ₁, ξ₂, ξ₃) には T^*E = E×V^* に対するアフィンフレームが必要ですが、もとのアフィンフレーム (a; v₁, v₂, v₃) の相反フレーム〈reciplocal frame〉(a, f₁, f₂, f₃) を取ります。相反フレームは次の等式で決まるT^*Eのアフィンフレームです。

$f_j(v_i) = \delta_{j\,i} \:\: i,j = 1,2,3$

微分幾何では、表示であるスカラーを並べる方向（縦横）というより、インデックス〈添字〉の上下位置で、接バンドルTEの要素と余接バンドルT^*Eの要素を区別しています。

僕は、接バンドルと余接バンドルを別物として明示的に定義したほうがいいとは思いますが、双対ベクトル空間を導入するのはけっこう敷居が高かったりするので、「接ベクトルとは違ったナニカ」が必要になったら「平面と法線」のメタファーを使うのも否定はしません。1次微分形式を、（層状の）平面の場や（目盛り付き）法線の場で（少なくとは感覚的な把握では）代用できます。

[追記 date="2020-11-28"]
次の図は、Wikipedia: ベクトルの共変性と反変性に載っていた図（の一部）です。

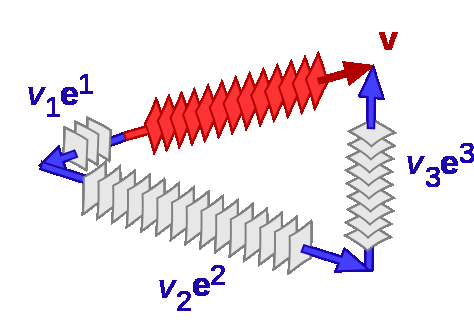
v, e¹, e², e³ は共変ベクトル、つまり余接ベクトルです。それぞれの共変ベクトルは、層状の平面達とそれを貫く法線を伴って描かれています。“反変ベクトル＝接ベクトル”は単なる矢印であるのに対して、“共変ベクトル＝余接ベクトル”は平面と法線のイメージ〈メンタルモデル〉を持つわけです。
[/追記]