2次元のコンピュータッド - 檜山正幸のキマイラ飼育記 (はてなBlog)

「コンピュータッドとそのモデル：同義語・類義語のジャングル」でコンピュータッドを紹介しました。2次元のコンピュータッドを中心に、もう少しコンピュータッドの話を続けます。一般次元のコンピュータッドをちゃんと定義することはしていません、だいぶ難しいので。 $\newcommand{\cat}[1]{ \mathcal{#1} }% \newcommand{\id}{ \mathrm{id} }% \newcommand{\Id}{ \mathrm{Id} }% \newcommand{\conc}{ \mathop{\#} }% \newcommand{\pto}{ \supseteq\!\to }% \newcommand{\delm}[2]{ \mathop{{,^{#1}_{#2}} } } \newcommand{\gconc}[2]{ \mathop{{\#^{#1}_{#2}} } } % generic concatenation \newcommand{\bbf}[1]{ \mathbb{#1} } \newcommand{\str}[1]{\mathrm{s}{#1}\text{-}}$

内容：

前回の記事からの記法変更
セルと射
図面と始図面／終図面
有限な2-コンピュータッド
2-コンピュータッドの0-図面、1-図面
2-コンピュータッドの2-図面の記述
2-コンピュータッドの連接演算
2-コンピュータッドから生成された自由厳密2-圏

前回の記事からの記法変更

コンピュータッドは厳密n-圏の生成系です*1が、球体集合〈globular set〉と深い関係があるので、球体集合の用語・記法が使われます。圏（高次圏含む）と球体集合の用語・記法には違いがあるので、ここで用語・記法をハッキリさせておきます。できるだけ共通の用語・記法に揃えます（完全に揃えるのは無理ですが）。

前回の記事「コンピュータッドとそのモデル：同義語・類義語のジャングル」からの記法の変更があります。「前回の記法 → 今回の記法」の形で箇条書きにまとめておきます*2。

$\Sigma_k$ → $|\Sigma|_k$ 　絶対値記号を付ける
$src_k, trg_k$ → $s_k, t_k$ 　一文字に短縮、s = source, t = target
$\bbf{F}_k$ → $\bbf{F}_k$ 　変更なし
$\bbf{U}_k$ → $\bbf{U}_k$ 　変更なし
$\Sigma_{\le k}$ → $\Sigma_{\le k}$ 　変更なし
$\bbf{F}_k(\Sigma_{\le k})$ → $\bbf{F}_k(\Sigma) = \bbf{F}_k\Sigma$ 　下付きの “ $\le k$ ” は省略
$\Sigma_k^*$ → $\Sigma_k^*$ 　変更なし $\Sigma_k^* = \bbf{F}_k\Sigma$

この記事で $Figure_k(\Sigma)$ という記法を導入してますが、次の関係があります。

$\quad Figure_k(\Sigma) = |\bbf{F}_k \Sigma|_k$

特に $k = 1$ では：

$\quad Figure_1(\Sigma) = |\bbf{F}_1 \Sigma|_1$

これは次のよく知られた関係です。詳しい事情は後述。

$\quad Path(\Sigma) = Mor(\bbf{F}_1 \Sigma)$

セルと射

以下、n, k は自然数で、 $0\le k \le n$ とします。

n-コンピュータッドも厳密n-圏も、各kごとにk次元の構成素〈constituent〉を持ちます。その構成素をk-射とかk-セルと呼びます。「k-射」と「k-セル」はたいていは同義語ですが、ここでは次のように約束します。

n-コンピュータッドのk次元の構成素をk-セル〈k-cell〉と呼ぶ。
厳密n-圏のk次元の構成素をk-射〈k-morphism〉と呼ぶ。

n = 2 の場合なら：

次元 k	2-コンピュータッドの構成素	厳密2-圏の構成素
0	0-セル＝頂点	0-射＝対象
1	1-セル＝辺	1-射＝射
2	2-セル＝面	2-射

$\Sigma$ がn-コンピュータッドのとき、そのk-セルの集合を $|\Sigma|_k$ と書くことにします。厳密n-圏 $\cat{C}$ の場合も、そのk-射の集合を $|\cat{C}|_k$ と書き、記法を揃えます。

0-射の集合： $|\cat{C}|_0 = |\cat{C}| = Obj(\cat{C})$
1-射の集合： $|\cat{C}|_1 = Mor(\cat{C})$
2-射の集合： $|\cat{C}|_2$

図面と始図面／終図面

0-コンピュータッドは単なる集合、1-コンピュータッドは有向グラフです。 $\Sigma$ が1-コンピュータッド（つまり有向グラフ）のときは：

$|\Sigma|_0$ は頂点の集合
$|\Sigma|_1$ は辺〈有向辺〉の集合

$A, B\in |\Sigma|_0$ に対して、頂点〈0-セル〉 $A$ から頂点〈0-セル〉 $B$ に至るパス〈道 | 経路〉を次の形で書くことにします。

$\quad [A/ e_1, \cdots, c_l / B]$

$A$ はパスの始点、 $B$ はパスの終点、 $l$ はパスの長さです。 $e_1, \cdots, c_l$ は辺の並びですが、隣り合う辺が“繋がっている”ものです。 $l = 0, l = 1$ のときのパスはそれぞれ次のようになります。

$\quad [A/ / B] \\ \quad [A/ e_1 / B]$

常に始点と終点を書くのは冗長ですが、明確さのために書いておきます。いずれ省略記法も導入します。

パスの一般次元版を、「図式〈diagram〉」と呼ぶことが多いですが、紛らわしいことが多くて難儀するので、「図面〈figure〉」という言葉を使います。「図面」もメチャクチャに一般的な言葉で、「図式」以上に曖昧多義的かも知れませんが、次元を添えて「k-図面〈k-figure〉」と呼べば曖昧性は減るでしょう。図面＝パスの一般次元版は、組み合わせ幾何的に言えば、連結な球体複体〈connected globular complex〉です。「k-図面」は、「k次元の連結な球体複体」の短縮別名と思ってください。

図面も各次元ごとに考えます。0-図面、1-図面、2-図面、‥‥ のように。現時点では、一般次元のk-図面を定義してませんが、1-図面が1次元の図形（有向折れ線）だったように、k-図面はk次元の多角形・多面体の塊〈cluster〉のようなものだと思ってください。特に、次元 0, 1 の場合なら次のようでした。

0-図面は0-セル〈頂点〉と同じ。
1-図面はパス。パスの始点と終点は0-図面で、パスは1-セル〈辺〉の組み合わせ。

一般次元では、始点／終点ではなくて始図面／終図面〈source figure / target figure〉という言葉を使いましょう。k-図面の表示は次のようになります。

$\quad [p/ \cdots / q]$

ここで、 $p$ は始図面である (k - 1)-図面で、 $q$ は終図面である (k - 1)-図面です。“ $\cdots$ ” の部分はk-セルの組み合わせが入るのですが、テキストで表示するのは難しいので省略しています。具体的な表示にはペースティング図を使います。

n-コンピュータッドのk-図面には、1次元低い次元の始図面と終図面が対応するわけですが、k-図面の始図面／終図面は、図面を構成するセルの始図面／終図面から計算します。セルに始図面／終図面を対応させる写像を以下のように書きます。

$\quad s_{k - 1}, t_{k - 1}: |\Sigma|_k \to Figure_{k - 1}(\Sigma) \:\text{ for }k = 1, \cdots, n$

ここで、 $Figure_{k - 1}(\Sigma)$ はコンピュータッド $\Sigma$ の(k-1)-図面の集合です。一般次元の図面を定義してないですが、全体的構造はこうなっている、ということです。 $s, t$ の添字を余域の次元にするのは単にそういう習慣なだけです（域の次元を添字にしてもかまいません）。

1-コンピュータッドの場合は、k = 1 （k - 1 = 0）しか意味がなく：

$\quad s_0, t_0: |\Sigma|_1 \to Figure_0(\Sigma)$

$Figure_0(\Sigma) = |\Sigma|_0$ なので、結局、

$\quad s_0, t_0: |\Sigma|_1 \to |\Sigma|_0$

が1-コンピュータッド構造のすべてです。 $\Sigma = (|\Sigma|_1, |\Sigma|_0, s_0, t_0)$ は有向グラフということになりますね。

圏〈1-圏〉 $\cat{C}$ は1-コンピュータッドとみなせて、そのとき $s_0 = dom,\, t_0 = cod$ です。

$\quad dom, cod: |\cat{C}|_1 \to |\cat{C}|_0$

これは、「圏は有向グラフとみなせる」という事実の再確認です。

2-コンピュータッドの場合は、k = 2 もあります。

2-コンピュータッドの1-図面の集合 $Figure_1(\Sigma) = Path(\Sigma)$ は、有向グラフ構造 $s_0, t_0: |\Sigma|_1 \to |\Sigma|_0$ をもとにキチンと定義できます。2-コンピュータッドなら、さほどの手間なく扱えそうです。まずは2-コンピュータッドを探るのは良い戦略でしょう。

有限な2-コンピュータッド

$|\Sigma|_0 = \{A, B, C\}$
$|\Sigma|_1 = \{f, g, h, k\}$
$|\Sigma|_2 = \{\alpha,\beta\}$
$s_0(f) = A, t_0(f) = B$
$s_0(g) = A, t_0(g) = B$
$s_0(h) = B, t_0(g) = C$
$s_0(k) = A, t_0(g) = C$
$s_1(\alpha) = [A/ f / B], t_1(\alpha) = [A/ g / B]$
$s_1(\beta) = [A/ f, h / B], t_1(\alpha) = [A/ k / B]$

今上に列挙した情報を、テキスト形式で次のように書くことにします。当該のコンピュータッドに Foo という（どうでもいい）名前を付けています。

2-computad Foo {
  0-cell A, B, C

  1-cell f:A → B
  1-cell g:A → B
  1-cell h:B → C
  1-cell k:A → C

  2-cell α::[A/ f /B] ⇒ [A/ g /B]
  2-cell β::[A/ f, h /C] ⇒ [A/ k /C]
}

2-コンピュータッドのテキスト形式の記述を見て、指標〈signature〉を思い出した人がいるかも知れません。実際、コンピュータッドと指標は同じものです。「コンピュータッド」と「指標」を強いて使い分けるなら、抽象的・組み合わせ的に定義された構造がコンピュータッドで、それをテキスト形式で記述したものが指標です。指標はテキスト形式記述であるとすると、その書き方であるテキスト構文が色々あります。同一のコンピュータッドを記述する、異なる構文（語彙と文法）のテキスト記述がたくさん出てくることになります。

2-コンピュータッドの0-図面、1-図面

2-コンピュータッドの0-図面は0-セルのこと、1-図面はパスのことでした。前節の例 Foo に関して言えば：

$Figure_0(Foo) = |Foo|_0 = \{A, B, C\}$
$Figure_1(Foo) = Path(Foo) = \{ [A//A], [B//B], [C//C], [A/ f /B], [A/f, g/C], \cdots \}$

0-図面に関しては特に言うことはありません。1-図面〈パス〉は次の3種類に分類します。

$[X//X]$ の形の1-図面を空1-図面〈empty 1-figure〉と呼ぶ。 $[X//X]$ を $\id_X$ と略記してよい。
$[X/e/Y]$ の形の1-図面を基本1-図面〈elementary 1-figure〉と呼ぶ。 $[X/e/X]$ を $[e]$ または単に $e$ と略記してよい。
$[X/e_1,\cdots, e_l/Y]$ の形で $l \ge 2$ の1-図面を複合1-図面〈compound 1-figure〉と呼ぶ。 $[X/e_1,\cdots, e_l/Y]$ を $[e_1, \cdots, e_l]$ と略記してよい。

空1-図面はほんとに空なわけではなくて、0セル〈頂点〉を持っています。1-セルを持ってないという意味での空です。

単一の1-セルだけを持つ基本1-図面に関しては次の条件があります。

$\quad s_0(e) = X, t_0(e) = Y$

複数の1-セルを持つ複合1-図面に関しては次の条件があります。

$s_0(e_1) = X, t_0(e_l) = Y$
$t_0(e_i) = s_0(e_{i+1}) \:\text{ for }1 \le i \lt l$

1-図面に対する始図面〈始点〉と終図面〈終点〉は次のように定義されます。

空1-図面： $s_0([X//X]) = X, t_0([X//X]) = X$
基本1-図面： $s_0([X/e/Y]) = X, t_0([X/e/Y]) = Y$
複合1-図面： $s_0([X/e_1, \cdots, e_l/Y]) = X, t_0([X/e_1, \cdots, e_l/Y]) = Y$

以上で、 $s_0, t_0:Path(\Sigma) = Figure_1(\Sigma) \to Figure_0(\Sigma) = |\Sigma|_0$ が完全に定義できました。

次に、1-図面〈パス〉の連接〈concatenation〉演算を定義します。連接の中置演算子記号を $\conc$ とします。 $(\conc)$ は中置演算子記号に対応する部分写像の意味です。

$\quad (\conc): Figure_1(\Sigma)\times Figure_1(\Sigma) \pto Figure_1(\Sigma)$

記号 “ $\pto$ ” は部分写像を表します。1-図面の連接は、単なるリストの連接とは違って、任意の2つの1-図面に対して定義できるわけではありません。 $p, q \in Figure_1(\Sigma)$ が連接可能である条件は次のとおりです。

$\quad t_0(p) = s_0(q)$

この条件を満たすときだけ $p \conc q \in Figure_1(\Sigma)$ が確定します。複合1-図面の連接は次のようです。

$\quad [X/e_1, \cdots, e_l/Y]\conc [Y/f_1, \cdots, f_m/Z] := [X/e_1, \cdots, e_l, f_1, \cdots, f_m/Z]$

空1-図面や基本1-図面が混じる場合も想像できるでしょう。

連接演算は、結合律と単位律を満たします。

連接の結合律： $(p\conc q) \conc r = p\conc (q \conc r)$
連接の左単位律： $\id_{s_0(p)}\conc p = p$
連接の右単位律： $p \conc \id_{t_0(p)}= p$

1-図面を記述するときの区切り記号であるカンマと連接の記号は置き換え可能です。例えば、

$\quad [X/e, f/Z] = [X/e/Y]\conc [Y/f/Z]$

略記を用いて書けば：

$\quad [e, f] = [e]\conc [f] = e\conc f$

複合1-図面は基本1-図面の連接として書けます。

2-コンピュータッドの2-図面の記述

2-コンピュータッドの2-図面は、2-セルの組み合わせです。1次元のときは、1-セルをカンマで区切って並べれば済みましたが、2次元になるとセルの組み合わせ方の記述が複雑になります。次の例を見てください。

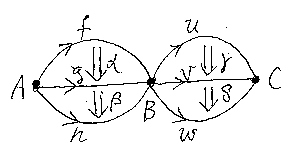
$\alpha$ と $\beta$ は、1-セル $g$ を境界（繋ぎ目）として“縦に”並んでいます。 $\alpha, \beta$ をひと塊とみた図形（部分2-図面）と、 $\gamma, \delta$ をひと塊とみた図形（部分2-図面）は、0-セル $B$ を境界として“横に”に並んでいます。

1次元境界で縦並びしている2-セルの区切り記号と、0次元境界で横並びしている2-図面の区切り記号は区別する必要があります。一般次元でも使えるように、次の区切り記号を導入します。

縦並びの区切り記号： $\delm{2}{1}$
横並びの区切り記号： $\delm{2}{0}$

一般的な $\delm{k}{b}$ は、k次元のセル／図面が、b次元の境界を挟んで並んでいるときに使う区切り記号です。 $b = 0$ のときは下付き $b$ を省略していいとします。上付きの $k$ も文脈から明らかなら省略してかまいません。

この区切り記号を使うと、上に図で示した2-図面は次のように記述できます。

$\quad [\, [A/ f\delm{1}{0} u /C] /\\ \qquad (\alpha \delm{2}{1} \beta)\\ \qquad \delm{2}{0}\\ \qquad (\gamma \delm{2}{1} \delta)\\ \quad /[A/ h\delm{1}{0} v /C] \,]$

区切り記号の添字で省略可能なものを省略すると：

$\quad [\, [A/ f , u /C] /\\ \qquad (\alpha \delm{}{1} \beta)\\ \qquad ,\\ \qquad (\gamma \delm{}{1} \delta)\\ \quad / [A/ h , v /C] \,]$

空図面以外では始図面／終図面を省略していいとすれば：

$\quad [ (\alpha \delm{}{1} \beta), (\gamma \delm{}{1} \delta) ]$

2次元だけの特別なルールとして、 $\delm{2}{1} = \delm{}{1}$ を $\mid$ で代用していいとすると：

$\quad [ (\alpha \mid \beta), (\gamma \mid \delta) ]$

あるいは、縦の並びは実際に縦に並べるなら：

$\quad [ \begin{pmatrix}\alpha \\ \beta\end{pmatrix}, \begin{pmatrix}\gamma \\ \delta\end{pmatrix} ]$

と、こんな具合に、なにやかにやと省略と工夫をして、2-図面をテキスト〈文字列〉形式で表そうと頑張ることになります。

2-コンピュータッドの連接演算

2-コンピュータッドの2-図面の場合、テキスト記述〈表示〉は一意には決まりません。縦の並びは縦に書くとして、次の異なる表示は同じ2-図面を表しています。

$\quad [ \begin{pmatrix}\alpha \\ \beta, \gamma \end{pmatrix} , \begin{pmatrix}\delta \\ \varepsilon \end{pmatrix} ]\\ \quad [ \begin{pmatrix}\alpha, \delta \\ \beta, \gamma, \varepsilon \end{pmatrix} ]$

1-図面〈パス〉の場合とは違って、表示の標準形〈正規形〉をうまく決めることも出来ません。異なる（表示としては異なる）2つのテキスト形式記述がどんなときに同じ2-図面を表しているかを決定する判断基準が必要です。

1-図面〈パス〉は、1-セル〈辺〉から出発して連接演算で書けました。連接演算の代数的な法則（結合律、単位律）は、1-図面の表示の同値性（同じ1-図面を表すこと）を決定するときに使われていました。同様に、2-図面の連接演算とその法則があれば、2-図面の表示の同値性を決定できるでしょう。2-図面の連接演算は、縦方向の連接と横方向の連接の2種類を考える必要があります。連接の演算子記号を次のように決めましょう。

縦方向の連接演算子記号： $\gconc{2}{1}$
横方向の連接演算子記号： $\gconc{2}{0}$

一般的な連接演算は $\gconc{k}{b}$ という記号です。k次元のセル／図面を、b次元の境界を挟んで連接する演算です。添字の省略規則は区切り記号 $\delm{k}{b}$ と同じとします。

区切り記号で記述された2-図面は、区切り記号を連接演算子記号に置き換えた式〈expression〉で表現できるので、先の例は次のように書けます。

$\quad (\alpha \gconc{2}{1} (\beta \gconc{2}{0} \gamma)) \gconc{2}{0} (\delta \gconc{2}{1} \varepsilon)\\ \:\\ \quad ( \alpha\gconc{2}{0} \delta) \gconc{2}{1} (\beta \gconc{2}{0} \gamma \gconc{2}{0} \varepsilon )$

次元の添字を省略すると、下付き 1 が付いている演算子が縦方向の連接になります。

$\quad (\alpha \gconc{}{1} (\beta \gconc{}{} \gamma)) \gconc{}{} (\delta \gconc{}{1} \varepsilon)\\ \:\\ \quad ( \alpha\gconc{}{} \delta) \gconc{}{1} (\beta \gconc{}{} \gamma \gconc{}{} \varepsilon )$

これらの連接演算（と空図面）を統制する代数的な法則は、厳密2-圏の代数的な法則（公理）になります。面倒な構成や証明を飛ばして結果だけ述べれば：

2-コンピュータッドの 0-図面、1-図面、2-図面の集合と連接演算 $\gconc{1}{0},\, \gconc{2}{1}, \gconc{2}{0}$ 、それと空1-図面、空2-図面達は、厳密2-圏となる。

2-コンピュータッドから生成された自由厳密2-圏

前節で述べた、2-コンピュータッド $\Sigma$ の 0-図面、1-図面、2-図面から構成される厳密2-圏を $\bbf{F}_2(\Sigma) = \bbf{F}_2 \Sigma$ と書きます。 $\bbf{F}_2 \Sigma$ の厳密な構成や公理的な特徴付けは述べてませんが、 $\bbf{F}_2 \Sigma$ の雰囲気くらいは伝わったと思います。

2-コンピュータッド $\Sigma$ の 0-図面、1-図面だけを考えると、1-コンピュータッド〈有向グラフ〉 $\Sigma_{\le 1}$ から生成された自由圏〈パスの圏〉を作れます。これを $\bbf{F}_1 \Sigma$ と書きます。2-コンピュータッド $\Sigma$ の 0-図面だけ $\Sigma_{\le 0}$ を考えた場合は、 $\bbf{F}_0 \Sigma = |\Sigma|_0$ です。

$\bbf{F}_k \Sigma$ は、厳密k-圏の対象になります。

$\bbf{F}_0 \Sigma \in |\str{0}{\bf Cat}| = |{\bf Set}|$
$\bbf{F}_1 \Sigma \in |\str{1}{\bf Cat}| = |{\bf Cat}|$
$\bbf{F}_2 \Sigma \in |\str{2}{\bf Cat}|$

$\bbf{F}_k$ は関手 $\bbf{F}_k: k\text{-}{\bf Compd} \to \str{k}{\bf Cat} \text{ in } {\bf CAT}$ へと拡張できて、忘却関手と一緒に自由忘却随伴系〈free-forgetful adjunction〉 $\bbf{F}_k \dashv \bbf{U}_k$ を構成します。