「タルスキーの最小プレ不動点定理(訂正)」において:
証明の流れを完全に追えるように、中間の命題にいちいち名前(ブラケットで囲った文言)を付けて参照することにします。
と、やってはみたのですが、“証明の流れ”がテキストで直列に(シリアライズされて)書かれているので、やっぱり“証明の流れを完全に追う”のは辛いかも知れません。テキストで直列に書く方式だと、証明のツリー構造がつぶれてしまうので、それを再現する労力で消耗します。
以下に、証明のツリー構造を Graphviz で描いた絵を示します。各ノードに対応する定義や命題は絵の下に箇条書きで並べています。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\Name}[1]{[#1] :\equiv }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
`$

[図のみ別に]
- $`\Name{P\: の要素はプレ不動点} \forall x\in X.\, x \in P \Iff f(x) \le x`$
- $`\Name{補題\: 1} x \in P \Imp f(x) \in P`$
- $`P`$ の最小元の存在を仮定
- $`\Name{a\: の定義} a := \mrm{least}(P)`$
- $`\Name{a\: は\: P \: の要素} a\in P`$
- $`\Name{a\: は最小元} \forall x\in X.\, x\in P \Imp a \le x`$
- $`\Name{不等式\: 1}f(a) \le a`$
- $`\Name{f(a)\: は\:P\: の要素} f(a) \in P`$
- $`\Name{不等式\: 2} a \le f(a)`$
- $`a = f(a)`$
- $`\Name{a\: は\:F\: の要素}a \in F`$
- $`\Name{補題\: 2} B\subseteq A \subseteq X \land l = \mrm{least}(A) \land l \in B \Imp l = \mrm{least}(B)`$
- $`\Name{結論} a = \mrm{least}(F)`$
内容的には「タルスキーの最小プレ不動点定理(訂正)」に書いた証明とまったく同じですが、ずっと分かりやすいのではないでしょうか。
僕もたいていは“テキストで直列に書く方式”で書くのですが、毎度心苦しい気がします。ツリー構造も描けば無駄に消耗することもないのは分かっているのですが、そこまで手間をかける気力がないので申し訳ない感じがするのです。言ってもしょうがないことだけど、ため息が出るわ。
上のツリー構造もけっこう省略はしていて、例えば、「不等式 1」と「不等式 2」から等式を出す部分は次のように描けばより正確です。
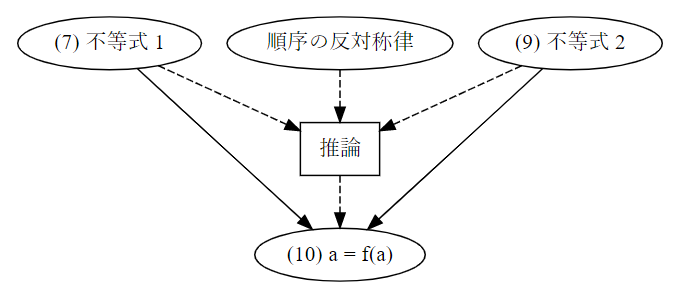
[図のみ別に]
実際は、順序集合の公理である反対称律も使って破線矢印のような推論をしてますが、そこは省略して実線矢印のように描いています。