依存アクテゴリーが面白い

とあるキッカケがあって、マッテーオ・カプチとディビッド・ジャズ・マイヤースの講演アブストラクトを眺めてみました。

• [CM23]
• Title: Constructing triple categories of cybernetic processes
• Authors: Matteo Capucci, David Jaz Myers
• Date: 2023/11/11
• Pages: 3p
• URL: https://act2023.github.io/papers/paper58.pdf

Applied Category Theory 2023 でのカプチによる発表の録画もあるようですが、その動画はまだ見てません。

• https://www.youtube.com/watch?v=jYxnUy1vH7Q

3ページ（実質2ページ）しかない概要では、定義もろくに書いてないので、想像で補って解釈するしかありません。その想像が間違っている可能性もありますが、カプチ／マイヤースが提案する圏類似代数構造〈category-like algebraic structure〉はとても面白そうです。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{\text{ in }}
\newcommand{\hyp}{\text{－} }
\newcommand{\F}[1]{ {{#1}^{-1}} } % fiber
\newcommand{\obj}[1]{ {{#1}\!\downarrow} }
\newcommand{\SPAN}{ {\mathbb{S}{\bf PAN}} }
\newcommand{\pto}{\dashrightarrow}
\newcommand{\twoto}{ \Rightarrow }
\newcommand{\o}[1]{ \overline{#1} }
\newcommand{\u}[1]{ \underline{#1} }
\newcommand{\NFProd}[3]{ \mathop{_{#1} \!\underset{#2}{\times}\,\!_{#3} } }
\newcommand{\dblcat}[1]{\mathbb{#1}}
`$

内容：

関連記事：

1. 依存アクテゴリーが面白い （この記事）
2. 依存アクテゴリーに向けて
3. 依存型理論の圏論的セマンティクスの資料
4. 環境付き計算と依存アクテゴリー 1/n
5. 環境付き計算と依存アクテゴリー 2/n

依存アクテゴリー

カプチ／マイヤースは、“モノイド圏が圏に作用する構造”であるアクテゴリー〈actegory〉を一般化した概念として反ラックス依存アクテゴリー〈oplax dependent actegory〉を提案しています。ちょっと名前が長過ぎますよね。それと、「反ラックス」という形容詞には次の問題があります。

「2階インデックス付き圏と反ラックス余錐」から：

この呼び名は、どちらかの方向をラックスと決めたら、もう一方を反ラックス（あるいは余ラックス）と呼ぶだけで、逆の呼び名もありえます。また、ラックスと反ラックスを区別しないこともあります。

形容詞「反ラックス」は取り去って、ここでは単に依存アクテゴリー〈dependent actegory〉と呼びます。

カプチ／マイヤースは、依存アクテゴリーと一般化Para構成〈generalized Para construction〉がオーガニックな（人為的な細工や、夾雑物が含まれない）*1概念であることを強調したいようです。

僕の“想像”が間違ってないなら、実際、依存アクテゴリーは正統派・王道的な概念に思われます。依存アクテゴリーは、かつて「モナド論をヒントに圏論をする（弱2-圏の割と詳しい説明付き）」で述べた代替圏／拡張圏の“ひとつの実現形態”として位置付けられる構造だと思います。

カプチ／マイヤースの依存アクテゴリーは、それを定義するだけでもだいぶ大変なので、依存アクテゴリーそのものではなくて、セッティングを単純にした概念を紹介します。単純化したセッティング〈状況設定 | 定義の環境〉とは、集合／関数／スパンで構成される二重圏です。この二重圏は、集合係数の行列をプロ射とする二重圏で、具体的な計算ができて分かりやすいものです。

集合係数の行列については、以下の過去記事で説明しています。

• スパンとファイバー積と行列計算
• 集合係数のスカラー・ベクトル・行列・テンソル
• 集合・関数係数行列の2-圏、モナドも添えて

集合圏のスパンの結合〈composition〉にはプルバックを使いますが、プルバックについては以下の記事の最初の2つの節「プルバックってなに？」「集合圏のプルバック」を参照してください。

• ファイバーの計算の動機としてのプルバック公式

集合圏のスパン

圏 $`\cat{C}`$ における次の形状の図式を、$`\cat{C}`$ のスパン〈span〉と呼びます。

$`\quad \xymatrix{
A
& X \ar[l]_f \ar[r]^g
& B
}\: \In \cat{C}
`$

以下、$`\cat{C} = {\bf Set}`$ と置きます。つまり、もっぱら集合圏のスパンを考えます。

集合圏のスパンは次のような写像と同じことです。$`\langle \hyp, \hyp \rangle`$ は、写像のデカルト・ペアリングです。

$`\quad \langle f, g\rangle : X \to A \times B \In {\bf Set}`$

これは、直積集合 $`A\times B`$ 上のバンドル（スライス圏 $`{\bf Set}/(A\times B)`$ の対象）とみなせます。バンドル-ファミリー対応（「バンドル-ファミリー対応 再考」と、そこからリンクされている記事達を参照）により、以下のようなファミリーとみなせます。

$`\quad M := R_{A\times B}(\obj{\langle f, g\rangle}) \; : A\times B \to |{\bf Set}| \In {\bf SET}`$

$`R_{A\times B}(\obj{\langle f, g\rangle})`$ という書き方の詳細は棚上げして、ファミリー $`M`$ は次のように、2つのインデックスを持つ集合族だと理解すれば十分です。

$`\text{For }(a, b) \in A\times B\\
\quad M_{a\, b} := \F{\langle f, g\rangle}(a, b) = \F{f}(a) \cap \F{g}(b) \;\in |{\bf Set}|
`$

2つのインデックスを持つということは行列なので、集合圏のスパンは集合係数の行列として書き下せます。

「スパンとファイバー積と行列計算」では、行列 $`M`$ を表すために、スパンの $`X`$ （ボディまたはヘッドと呼ぶ）をオーバーロード〈名前の多義的使用〉した記号の乱用をしています。

$`\text{For }(a, b) \in A\times B\\
\quad X_{a\, b} := \F{f}(a) \cap \F{g}(b) \;\in |{\bf Set}|
`$

スパンと集合係数の行列を同一視（意図的に混同）した言い方をすると、プルバックを使ったスパンの結合は、行列の掛け算となります。ただし、掛け算記号はファイバー積の記号 $`\times_B`$ を使い、図式順中置演算子記号として使います。掛け算の結果〈行列の積〉 $`Z = X \times_B Y`$ の成分表示は次のようです。

$`\quad Z_{a\, c} = X_{a\, *} \times_B Y_{*\, c} = \sum_{b \in B} (X_{a\, b} \times Y_{b\, c})`$

詳しくは「スパンとファイバー積と行列計算」を見てください。

記号の乱用をしないでスパンを記述したいときは、スパンを $`S, T, U`$ などラテン・アルファベット後半の大文字で表すことにして、
$`\quad S = (A \overset{f}{\leftarrow} X \overset{g}{\to} B \:\In {\bf Set})`$
のように書きます。

スパンの構成素は次のような記法で参照します*2。

• スパン $`S`$ のボディ〈body〉または頭部〈head | ヘッド〉： $`\mrm{Body}(S) := X`$
• スパン $`S`$ の左足〈left foot〉： $`\mrm{Left}(S) := A`$
• スパン $`S`$ の右足〈right foot〉： $`\mrm{Right(S)} := B`$
• スパン $`S`$ の左脚〈left leg〉： $`\mrm{l}_S := f \;: X \to A`$
• スパン $`S`$ の右脚〈right leg〉： $`\mrm{r}_S := g\; : X \to B`$

$`\quad S = (\mrm{Left}(S) \overset{l_S}{\leftarrow} \mrm{Body}(S) \overset{r_S}{\to} \mrm{Right}(S) \:\In {\bf Set})`$

このような記法の背景（前層／余前層）については「木と林（有向グラフ） // グラフの圏と反射的グラフの圏」に書いています。

スパンの2-圏と二重圏

「スパン」は集合圏のスパンのことだとします。左右の足を $`A, B`$ に固定するとして、スパン $`R, S`$ のあいだの準同型射〈homomorphism〉は次の図式を可換にする写像 $`\alpha`$ のことです。

$`\quad \xymatrix{
{}
& X \ar[dd]|{\alpha} \ar[dl] \ar[dr]
& {}
\\ A
&{}
& B
\\
{}
& Y \ar[ul] \ar[ur]
& {}
}\\
\quad \text{commutative }\In {\bf Set}\\
\quad \text{where }X = \mrm{Body}(R),\: Y = \mrm{Body}(S)
`$

$`A, B`$ を両足とするスパンの全体は、スパンのあいだの準同型射を射として圏を形成するので、その圏を $`{\bf SPAN}(A, B)`$ とします。一方、
$`\quad R\in |{\bf SPAN}(A, B)|,\; T\in |{\bf SPAN}(B, C)|`$
のあいだにはプルバックによる結合（行列の掛け算） $`R \times_B T`$ があるので、全体として2-圏〈双圏〉*3となります。この2-圏を $`{\bf SPAN}`$ と書きます。

名前が全部大文字なのは、ホム圏が小さい圏ではないからです。スパンの圏には、サイズの問題や演算の緩さ〈looseness〉の問題があります。それについては以下の記事で書いています。が、サイズ／緩さは今は気にしないことにします。

• 圏のサイズと緩さと豊穣圏

スパン達は、二重圏に仕立てることもできます。二重圏の基本的概念・用語法は以下の記事達の約束に従います。

• 二重圏、縦横をもう一度
• 二重圏の縦横 補遺

スパン達の二重圏の対象は集合で、プロ射はスパンです。タイト射は関数〈写像〉です。二重射〈2-射〉はスパンの射になります。プロ射を破線矢印として、スパン達の二重圏の二重射とフレーム〈境界〉を描くと：

$`\quad \xymatrix{
A \ar[d]_{f} \ar@{-->}[r]^R
\ar@{}[dr]|{\alpha\, \Downarrow\:}
& B \ar[d]^{g}
\\
C \ar@{-->}[r]_S
& D
}`$

この二重射を集合圏内に展開すれば、次の可換図式です。

$`\quad \xymatrix{
A \ar[d]_{f}
& X \ar[l] \ar[r] \ar[d]|{\alpha}
& B \ar[d]^{g}
\\
C
& Y \ar[l] \ar[r]
& D
}\\
\quad \text{commutative }\In {\bf Set}\\
\quad \text{where }X = \mrm{Body}(R),\: Y = \mrm{Body}(S)
`$

集合圏のスパンをプロ射とする二重圏は $`\SPAN`$ と書くことにします。

二重圏 $`\SPAN`$ の二重射 $`\alpha`$ のフレーム〈境界〉のタイト射が両方とも恒等射のとき、次のように描きます。

$`\quad \xymatrix{
A \ar@{=}[d] \ar@{-->}[r]^R
\ar@{}[dr]|{\alpha\, \Downarrow\:}
& B \ar@{=}[d]
\\
A \ar@{-->}[r]_S
& B
}\\
\quad \In \SPAN
`$

このような退化した二重射を、エドワード・モアハウス〈Edward Morehouse〉*4
に従い、円板〈disk〉と呼びましょう。その理由は、縦のイコール記号を潰すと次の形になるからです。

$`\quad \xymatrix@C+1pc{
A \ar@{-->}@/^1.5pc/[r]^R
\ar@{}[r]|{\alpha\, \Downarrow\:}
\ar@{-->}@/_1.5pc/[r]_S
& B
}\\
\quad \In \SPAN
`$

この場合、プロ射が円周として残るのでプロ円板〈pro-disk〉と呼び、タイト射が残るタイト円板〈tight-disk〉と区別したほうが良いでしょう。

二重圏 $`\SPAN`$ のなかのプロ円板だけを考えると、それは2-圏 $`{\bf SPAN}`$ と同じものになります。2-圏 $`{\bf SPAN}`$ はタイト射が恒等射しかない二重圏と考えることができます。また、2-圏 $`{\bf SPAN}`$ は二重圏 $`\SPAN`$ のなかに埋め込めます。「円板 ←→ 四角形」の対応をイメージしましょう。

例： グラフと状態遷移系

スパンは、左足から右足へのプロ射として $`R: A \pto B`$ のように書けます。特に $`A = B`$ のとき、自己スパン〈endo-span〉と呼びます。集合圏の自己スパンは、$`A\times A`$ でインデックスされた正方行列として行列表示できます。自己スパンのプロ結合（プロ方向の結合、行列の積）はまた自己スパンになります。

（集合圏の）自己スパンの例を挙げます。まず、簡単な例*5はグラフ〈graph | 有向グラフ〉です（「木と林（有向グラフ） // グラフの圏と反射的グラフの圏」参照）。頂点集合が $`V`$ であるグラフ $`G`$ は次の形です。

$`\quad V \overset{\mrm{src}_G}{\longleftarrow} \mrm{Edge}(G) \overset{\mrm{trg}_G}{\longrightarrow} V \In {\bf Set}`$

したがってグラフは、辺集合がボディ、左脚がソース写像、右脚がターゲット写像である自己スパンとなります。自己スパンの結合をグラフの場合に図示すると次のようです（必要なら、「ファイバーの計算の動機としてのプルバック公式」を参照）。$`\o{G}`$ は $`\mrm{Edge}(G)`$ の略記（アーマン／チャップマン／ウウスタルの記法*6）です。

$`\quad \xymatrix{
% 1
{}
& {}
& {\o{G}\times_V \o{G}} \ar[dl] \ar[dr] \ar@{}[dd]|{\text{p.b.}}
& {}
& {}
\\% 2
{}
& {\o{G}} \ar[dl] \ar[dr]_{\mrm{trg}}
& {}
& {\o{G}} \ar[dl]^{\mrm{src}} \ar[dr]
& {}
\\% 3
{V}
& {}
& {V}
& {}
& {V}
}\\
\quad \In {\bf Set}
`$

自己スパンのプロ結合であるファイバー積 $`\o{G}\times_V \o{G}`$ （もっと正確に書けば、$`\o{G}\NFProd{\mrm{trg}}{V}{\mrm{src}}\o{G}`$、「ファイバーの計算の動機としてのプルバック公式 // プルバックってなに？」を参照）は、辺のペアで終点と始点が一致するもの（長さ 2 のパス）達の集合です。

もうひとつの（集合圏の）自己スパンの例として状態遷移系〈state transition system〉を挙げます。状態遷移系については「状態遷移系としての前層・余前層・プロ関手 // 状態遷移系」を参照してください。ここでは、右状態遷移系〈right state transition system〉 $`(M, S, \rho)`$ を考えます。

右状態遷移系 $`R = (M, S, \rho)`$ の構成素は：

• 右状態遷移系 $`R`$ の右刺激モノイド〈right stimuli monoid〉： $`\mrm{RStim}(R) := M`$
• 右状態遷移系 $`R`$ の状態空間〈state space〉： $`\mrm{SS}(R) := S`$
• 右状態遷移系 $`R`$ の右作用〈right action〉： $`\mrm{ract}_R := \rho\; : S\times \u{M} \to S`$

右刺激モノイド $`M`$ の構成素は次のように書くことにします。

• モノイド $`M`$ の台集合〈underlying set〉： $`\u{M}`$
• モノイド $`M`$ のモノイド演算〈monoid operation〉： $`(;) : \u{M}\times \u{M} \to \u{M}`$
• モノイド $`M`$ の単位元〈unit〉： $`e\in \u{M}`$

モノイド演算の中置演算子記号が '$`;`$' なのは、モノイドを単一対象の圏とみなしているからです。単位元は、唯一の対象の恒等射です。

右状態遷移系の右作用 $`\mrm{ract}_R`$ を '$`\cdot`$' で略記します。右作用の法則〈公理〉は次のように書けます。

$`\text{For }m,n \in \u{M}, s\in S\\
\quad s\cdot (m;n) = (s\cdot m)\cdot n\\
\quad s\cdot e = s
`$

右状態遷移系 $`R`$ が定義するスパンは次の形です。

$`\quad S \overset{\pi_1}{\longleftarrow} S\times \u{M} \overset{\mrm{ract}_R}{\longrightarrow} S \In {\bf Set}`$

$`\pi_1 =\pi^{S, \u{M}}_1`$ は直積の第一射影です。

自己スパンの結合を右状態遷移系の場合に図示すると次のようです。

$`\quad \xymatrix{
% 1
{}
& {}
& {(S\times \u{M}) \times_S (S\times \u{M})} \ar[dl] \ar[dr] \ar@{}[dd]|{\text{p.b.}}
& {}
& {}
\\% 2
{}
& {S \times \u{M} } \ar[dl] \ar[dr]_{\mrm{ract}}
& {}
& {S \times \u{M}} \ar[dl]^{\pi_1} \ar[dr]
& {}
\\% 3
{S}
& {}
& {S}
& {}
& {S}
}\\
\quad \In {\bf Set}
`$

自己スパンのプロ結合であるファイバー積 $`(S\times \u{M}) \times_S (S\times \u{M})`$ （より正確には、$`(S\times \u{M})\NFProd{\mrm{ract}}{S}{\pi_1}(S\times \u{M})`$）は、次の集合です。

$`\quad \{( (s, m), (t, n) ) \in (S\times \u{M}) \times_S (S\times \u{M}) \mid s\cdot m = t\}`$

つまり、$`S\times \u{M}\times \u{M}`$ と同型な集合です。

二重圏内のモノイドと2-圏内のモナド

二重圏内のモノイドについては、

• ヒューズ・アローと丹原プロ関手 // 二重圏内のモノイド

で述べています。が、特殊な事例に沿って説明しているので、一般論として再度繰り返します。

老婆心で注意しておくと、用語「モノイド」は多義的で、今まで使ってきたモノイドは集合圏のなかで定義される代数構造でしたが、この節の「モノイド」は一般的二重圏のなかで定義される抽象的代数構造です。類似性はありますが、別物です。

二重圏 $`\dblcat{D}`$ 内のモノイド〈monoid〉は、次の構成素からなります。以下で使っている二重射のテキスト記法は、見ればわかるでしょうが、「添加仮想二重圏 // 添加仮想二重圏の2-射のフレーム」で定義してます。

• モノイドの基礎対象〈ground object〉： $`A \in |\dblcat{D}|`$
• モノイドの台プロ射〈underlying promorphism〉： $`M : A \pto A \In \dblcat{D}`$
• モノイドの乗法二重射〈multiplication doublemorphism〉： $`\mu :: \mrm{id}_A[M \otimes M \twoto M]\mrm{id}_A \In \dblcat{D}`$
• モノイドの単位二重射〈unit doublemorphism〉： $`\eta :: \mrm{id}_A[\mrm{I}_A \twoto M]\mrm{id}_A \In \dblcat{D}`$

これらを図示すると：

$`\quad \xymatrix{
A \ar@{-->}[r]^{M} \ar@{=}[d]
\ar@{}[drr]|{\mu\,\Downarrow\:}
&A \ar@{-->}[r]^{M}
&A \ar@{=}[d]
\\
A \ar@{-->}[rr]_{M}
&{}
&A
}\\
\In \dblcat{D}
`$

$`\quad \xymatrix{
A \ar@{-->}[r]^{\mrm{I}_A} \ar@{=}[d]
\ar@{}[dr]|{\eta\,\Downarrow\:}
&A \ar@{=}[d]
\\
A \ar@{-->}[r]_{M}
&A
}\\
\In \dblcat{D}
`$

ここで、

• $`\mrm{id}_A`$ は、対象 $`A`$ に対するタイト方向の恒等射で、図では縦方向のイコール記号で表している。
• $`\otimes`$ は、プロ方向の結合〈プロ結合〉。
• $`\mrm{I}_A`$ は、単位プロ射。プロ方向の恒等プロ射。

上記の構成素の組 $`(M, \mu, \eta)/A`$ が、通常のモノイド（あるいはモナド）と同様な結合律、左右の単位律を満たすとき、$`(M, \mu, \eta)/A`$ を $`\dblcat{D}`$ 内のモノイド〈monoid〉といいます。

モノイドの結合律／単位律は、ペースティング図のポアンカレ双対であるストリング図で描くほうが分かりやすいです*7。

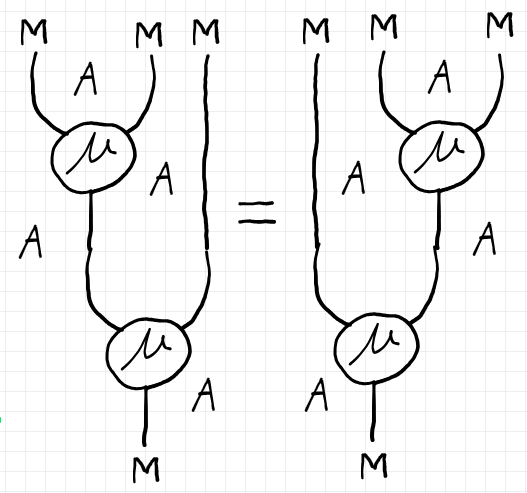
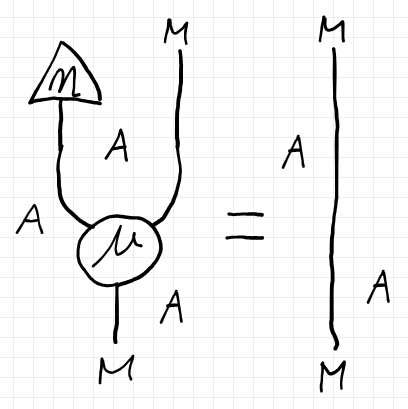
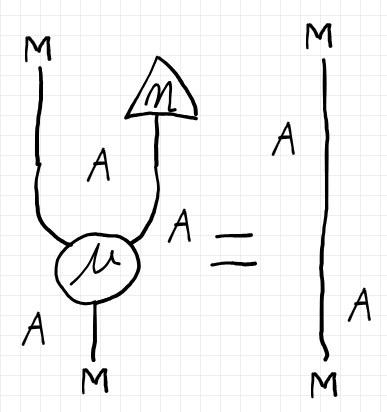
モノイドのあいだの準同型射〈モノイド射〉も定義できます。二重圏 $`\dblcat{D}`$ 内のモノイド達とそのあいだのモノイド射の全体は圏を形成します。この圏を $`\mrm{Mon}(\dblcat{D})`$ とします。

2-圏では、同様な構造をモナド〈monad〉と呼びます。2-圏を二重圏に埋め込むと、2-圏のモナドは二重圏のモノイドになります。「モノイド」「モナド」という呼び名の違いは単に歴史的経緯（偶然）によるものです*8。2-圏のモナドと二重圏のモノイドは、事実上同じ概念です。2-圏のモナドの理論は、二重圏のモノイドの理論として展開できます。

スパンの二重圏内のモノイドは圏

「集合・関数係数行列の2-圏、モナドも添えて」において、

小さい圏とは、集合・関数係数行列2-圏におけるモナドです。

と書きました。この過去記事の「集合・関数係数行列2-圏におけるモナド」と「モナドと圏」の節で、小さい圏と集合・関数係数行列2-圏内のモナドが同一の概念であることを詳しく説明しています。

集合・関数係数行列2-圏とは、（集合圏の）スパンの2-圏のことです。“スパンの2-圏内のモナド”と“スパンの二重圏内のモノイド”は同じものです。つまり、“小さい圏”と“スパンの二重圏内のモノイド”は同じものです。

念の為、与えられた小さい圏 $`\cat{C}`$ が、どのような“スパンの二重圏内のモノイド”になるか？ を復習しましょう。まず、圏 $`\cat{C}`$ は、$`\mrm{dom}, \mrm{cod}`$ によってグラフとみなせます。グラフは自己スパンでした。

$`\quad |\cat{C}| \overset{\mrm{dom}}{\longleftarrow} \o{\cat{C}} \overset{\mrm{cod}}{\longrightarrow} |\cat{C}| \In {\bf Set}`$

ここで、$`\o{\cat{C}}`$ は $`\mrm{Mor}(\cat{C})`$ の略記です（アーマン／チャップマン／ウウスタルの記法）。このスパンのことも $`\cat{C}`$ という名前で参照します（記号の乱用、オーバーロード）。

圏の結合を $`\mu`$ と書くと、次のプロファイル〈域・余域の仕様〉を持ちます。

$`\quad \mu : \o{\cat{C}} \NFProd{\mrm{cod}}{|\cat{C}|}{\mrm{dom}} \o{\cat{C}}
\to \o{\cat{C}}
\In {\bf Set}`$

これを、スパンの二重圏 $`\SPAN`$ のなかに移してみれば：

$`\quad \xymatrix{
|\cat{C}| \ar@{-->}[r]^{\cat{C}} \ar@{=}[d]
\ar@{}[rrd]|{\mu\, \Downarrow\:}
& |\cat{C}| \ar@{-->}[r]^{\cat{C}}
& |\cat{C}| \ar@{=}[d]
\\
|\cat{C}| \ar@{-->}[rr]_{\cat{C}}
& {}
& |\cat{C}|
}\\
\quad \In \SPAN
`$

圏の恒等を $`\eta`$ と書くと、次のプロファイルを持ちます。

$`\quad \eta : |\cat{C}| \to \o{\cat{C}} \In {\bf Set}`$

写像 $`\eta`$ を、恒等スパンからスパン $`\cat{C}`$ へのスパン準同型射とみなします。

$`\quad \xymatrix{
|\cat{C}| \ar@{=}[d]
& |\cat{C}| \ar[l]_{\mrm{id}} \ar[r]^{\mrm{id}}
\ar[d]|{\eta}
& |\cat{C}| \ar@{=}[d]
\\
|\cat{C}|
& \o{\cat{C}} \ar[l]^{\mrm{dom}} \ar[r]_{\mrm{cod}}
& |\cat{C}|
}\\
\quad \In {\bf Set}
`$

これを、スパンの二重圏 $`\SPAN`$ のなかに移してみれば：

$`\quad \xymatrix{
|\cat{C}| \ar@{-->}[r]^{\mrm{I}_{|\cat{C}|} }\ar@{=}[d]
\ar@{}[dr]|{\eta\,\Downarrow\:}
&|\cat{C}| \ar@{=}[d]
\\
|\cat{C}| \ar@{-->}[r]_{\cat{C}}
&|\cat{C}|
}\\
\In \SPAN
`$

二重圏 $`\SPAN`$ 内の構造 $`(\cat{C}, \mu, \eta)/|\cat{C}|`$ がモノイドの法則〈公理〉を満たすことは、もとの $`\cat{C}`$ が圏の法則を満たすことと同値です。

状態遷移系から作るスパンの二重圏内のモノイド

前の節「例： グラフと状態遷移系」において、右状態遷移系 $`R = (M, S, \rho)`$ からスパン（$`\SPAN`$ のプロ射）を作りました。単なるスパンではなくて、二重圏内のモノイドに仕立てることが出来ます。

二重圏内のモノイド（集合圏のモノイド $`M`$ ではない）の乗法 $`\mu`$ は次の写像として定義します。

$`\quad \mu : S\times \u{M}\times \u{M} \to S\times \u{M} \In {\bf Set}\\
\text{For }(s, m, n)\in S\times \u{M}\times \u{M} \\
\quad \mu(s, m, n) := (s\cdot m, n ) \; \in S\times \u{M}
`$

次の同型がありました。

$`\quad (S \times \u{M}\times \u{M}) \cong (S\times \u{M}) \NFProd{\rho}{S}{\pi_1} (S\times \u{M}) \In {\bf Set}`$

この同型により、$`\mu`$ を次の写像とみなします。

$`\quad \mu : (S\times \u{M}) \NFProd{\rho}{S}{\pi_1} (S\times \u{M}) \to (S\times \u{M}) \In {\bf Set}
`$

記法を簡潔にする目的で、一時的に $`X := (S\times \u{M})`$ と置きます。

$`\quad \mu : X \NFProd{\rho}{S}{\pi_1} X \to X \In {\bf Set}
`$

$`\mu`$ の域は、以下のようなスパンの結合です

$`\quad \xymatrix{
% 1
{}
& {}
& { X \times_S X } \ar[dl] \ar[dr] \ar@{}[dd]|{\text{p.b.}}
& {}
& {}
\\% 2
{}
& {X} \ar[dl] \ar[dr]_{ \rho }
& {}
& {X} \ar[dl]^{\pi_1 } \ar[dr]
& {}
\\% 3
{S}
& {}
& {S}
& {}
& {S}
}\\
\quad \In {\bf Set}
`$

さらに、
$`\quad S \overset{\pi_1}{\longleftarrow} X \overset{\rho}{\longrightarrow} S \In {\bf Set}`$
というスパンを $`R`$ という名前（右状態遷移系の名前）で参照します（記号の乱用、オーバーロード）。すると、$`\mu`$ は次のような二重射を定義します。

$`\quad \xymatrix{
S \ar@{-->}[r]^{R} \ar@{=}[d]
\ar@{}[rrd]|{\mu\, \Downarrow\:}
& S \ar@{-->}[r]^{R}
& S \ar@{=}[d]
\\
S \ar@{-->}[rr]_{R}
& {}
& S
}\\
\quad \In \SPAN
`$

二重圏内のモノイドの単位 $`\eta`$ は次の写像として定義します。

$`\quad \eta : S \to X = S\times \u{M} \In {\bf Set}\\
\text{For }s\in S \\
\quad \eta(s) := (s, e ) \; \in X = S\times \u{M}
`$

$`\eta`$ を次のようなスパン準同型射とみなします。

$`\quad \xymatrix{
S \ar@{=}[d]
& S \ar[l]_{\mrm{id}} \ar[r]^{\mrm{id}}
\ar[d]|{\eta}
& S \ar@{=}[d]
\\
S
& X \ar[l]^{\pi_1} \ar[r]_{\rho}
& S
}\\
\quad \In {\bf Set}
`$

これを二重圏 $`\SPAN`$ に移せば：

$`\quad \xymatrix{
S \ar@{=}[d] \ar@{-->}[r]^{\mrm{I}_S}
\ar@{}[dr]|{\eta\,\Downarrow\:}
& S \ar@{=}[d]
\\
S \ar@{-->}[r]_{R}
& S
}\\
\quad \In \SPAN
`$

このようにして定義した二重圏 $`\SPAN`$ 内の構造 $`(R, \mu, \eta)/S`$ がモノイドの法則〈公理〉を満たすことは、もとの $`R`$ が右状態遷移系の法則を満たすことと同値です。

右状態遷移系はスパンの二重圏内のモノイドになります。スパンの二重圏内のモノイドは小さな圏だったので、右状態遷移系は圏になります。右状態遷移系から直接的に圏を作りたいなら、群作用から作用亜群〈action groupoid〉を作る要領で、状態遷移系の作用圏〈action category〉を構成できます。

依存アクテゴリーへの道

ここまで話は、集合圏のスパンから出発していました。集合圏の代わりに圏達の2-圏 $`{\bf CAT}`$ を採用し、$`{\bf CAT}`$ のスパンから出発する議論もできそうです。集合は0次元の圏だったので、0次元から1次元へと“次元をひとつ上げた”議論になります。圏論で“次元をひとつ上げる”ことは、とんでもなく大変なことがあります。安直なアナロジーが成立するわけではありません。

しかし、次のような対応はありそうです。

• モノイド ←→ モノイド圏
• 状態遷移系 ←→ アクテゴリー
• 通常の圏 ←→ 弱二重圏〈スード二重圏〉*9

依存アクテゴリーは、アクテゴリーと弱二重圏の中間に位置する構造のように思えます。依存アクテゴリーやその仲間たちが住んでいる世界〈アビタ | 生息地〉は3次元の世界です。

2次元／3次元の世界での計算はシンドイのですが、カプチ／マイヤース（その他多くの人々）は、サイバネティック・プロセス（制御可能な動的システム）をモデルとしているので、具体的な実現・実装を想定することができます。シンドイ計算の結果は、具体的に解釈可能なモノかも知れません。

*1:「自然な〈natural〉」という形容詞が、自然変換の意味の自然性と誤解されそうなとき、人為的ではないという意味で「オーガニック」を、人間にとって違和感が少ないの意味なら「エルゴノミック」を使うことがあります。

*2:口頭で、「足」と「脚」を区別するには「脚」を「きゃく」と読むといいでしょう。

*3:ここでの「2-圏」は厳密2-圏のことではなくて、弱2-圏のことです。したがって、「2-圏」と「双圏」は同義語です。

*4:例えば Cartesian Gray-Monoidal Double Categories

*5:[追記]すべての自己スパンはグラフとみなせるので、簡単な例も複雑な例もグラフです。「簡単な」は、「グラフだと思えば、（心理的に）簡単でしょ」ということです。[/追記]

*6:例えば、「複余有向コンテナ〈オペラッドコンテナ〉によるオペラッドの定義」で使っています。

*7:このストリング図は、0-射を背景領域として描いているので、二重圏というより2-圏におけるストリング図です。モノイド〈モナド〉に関しては、二重圏でも2-圏でも変わりはありません。

*8:二重圏でも「モナド」と呼ぶこともあるでしょう。

*9:「弱」「スード」は、プロ方向の結合の法則が厳密に〈等式として〉成立するとは限らないことを意味します。単に「二重圏」と言った場合、厳密二重圏か弱二重圏かは人により場合により違います。