環境付き計算と依存アクテゴリー 2/n - 檜山正幸のキマイラ飼育記 (はてなBlog)

「環境付き計算と依存アクテゴリー 1/n」の続きです。$`\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{\text{ in }}
%\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\twoto}{ \Rightarrow }
\newcommand{\id}{ \mathrm{id} }
\newcommand{\hyp}{\text{－} }
\newcommand{\NFProd}[3]{ \mathop{_{#1} \!\underset{#2}{\times}\,\!_{#3} } }
%\newcommand{\dblcat}[1]{\mathbb{#1}}
\newcommand{\strdiag}[1]{ \mathscr{#1} }
\newcommand{\coupl}{ \circledast }
`$

内容：

デカルト・ストリング図と経路行列の方法
修正ミックス操作
環境付き計算ペアのカップリング
演算達が出揃った

ハブ記事：

環境付き計算と依存アクテゴリー 1/n

デカルト・ストリング図と経路行列の方法

「環境付き計算と依存アクテゴリー 1/n」を一瞥すれば分かるように、デカルト圏における計算には絵算〈ストリング図の計算〉をヘビーに使っています。（少なくとも僕は）テキスト数式の計算ではとても手に負えないです。

$`\cat{C}`$ をデカルト圏〈デカルト・モノイド圏〉として、$`\mrm{Poly}(\cat{C})`$ を標準的な方法で作った多圏（「述語論理：様々な多圏達の分類整理」参照）だとします。

以下のような“基本素子”、あるいはスパイダー（「述語論理：様々な多圏達の分類整理 // 補足：スパイダー」参照）を含んだストリング図をデカルト・ストリング図〈Cartesian string diagram〉と呼ぶとして、デカルト・ストリング図は多圏 $`\mrm{Poly}(\cat{C})`$ の多射〈poly {morphism | map | arrow}〉を表します。

名称	象形文字
対象または恒等射	$`\mrm{I}_A`$
対称射、スワップ、交差	$`\mrm{X}_{A, B}`$
対角射、コピー、分岐	$`\Delta_A`$
終射、削除、終端	$`!_A`$
選ばれた生成射	ラベル付きのボックス〈ノード〉

$`\strdiag{D}`$ がデカルト・ストリング図だとして、$`\strdiag{D}`$ が表す多射〈P.M. = polymorphism〉を $`\mrm{PM}(\strdiag{D})`$ とします。我々は、次のメタ定理を信じて絵算をしてます。

デカルト・ストリング図 $`\strdiag{D}`$ をデカルト・ストリング図 $`\strdiag{E}`$ へと“変形”できるならば、$`\mrm{PM}(\strdiag{D}) = \mrm{PM}(\strdiag{E})`$ である。

ここで言う“変形”は、デカルト圏の公理に基づく可逆な変形です。例えば、（象形文字を使ったテキストですけど）以下の双方向変形は“変形”の一例です。

$`\quad \Delta_A;(\mrm{I}_A \times !_A) \longleftrightarrow \mrm{I}_A
`$

上記メタ定理を（暗黙にであれ）前提としているので、$`\strdiag{D}`$ から $`\strdiag{E}`$ への“変形”が見つかれば、$`\mrm{PM}(\strdiag{D}) = \mrm{PM}(\strdiag{E})`$ が証明できたとみなします。

それはいいんですけども、“変形”を見つけるのがけっこう大変なことがあります。例えば以下は、実際に僕が出会った例です。左右は等しいでしょうか？

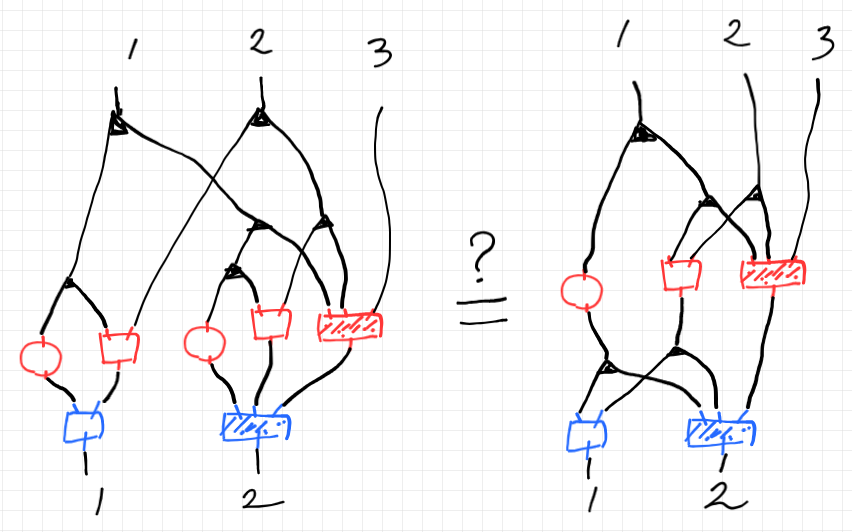
見た感じでは等式が成立しそうですが、変形ステップをキチンと書き出すのは面倒です。なんか楽できる方法はないでしょうか？

ここから先は、僕の経験則、あるいは発見的方法です。おそらく、メタ定理として成立していると思うのですが、現状ちゃんと確認してるわけではないし、参照できる文献もありません（頑張って探せばありそうだけど）。

上の事例のストリング図で、射の方向は上から下で、デカルト積の方向は左から右です。サイクルは生じないので、グラフとしては無サイクル〈非循環 | 非輪状〉有向グラフ〈DAG | ダグ）です。上側の入力ポート（番号が付いている）から、下側の出力ポートに至る経路は有限で、列挙できます。

例えば、入力 1 から出力 1 と、入力 1 から出力 2 への経路を列挙した集合は次のようです。経路に交差、分岐、終端は含めません。

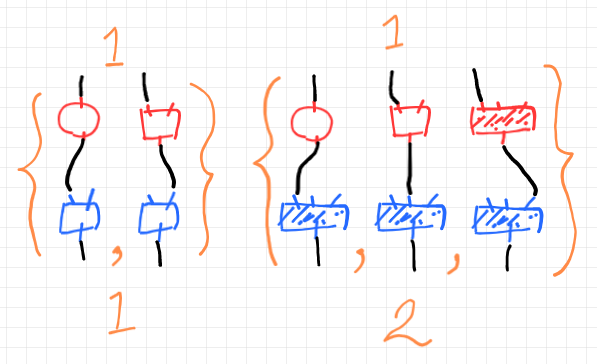
入力 $`i`$ から出力 $`j`$ に至る経路の集合を $`D[i, j]`$ とすると、これは集合を成分とする行列になります。デカルト・ストリング図 $`\strdiag{D}`$ から作られた経路集合の行列を $`\mrm{PathMat}(\strdiag{D})`$ とします。

$`\strdiag{D}`$ から $`\strdiag{E}`$ への“変形”が存在することを $`\cong`$ で書くことにすると、僕が成立を期待しているメタ命題（予想）は次です。

$`\quad \strdiag{D}\cong \strdiag{E} \iff \mrm{PathMat}(\strdiag{D}) = \mrm{PathMat}(\strdiag{E})
`$

組み合わせ的議論でゴリゴリ頑張ればなんとかなる気もしますがちょっと僕の体力が足りない。

予想が外れたとしても、経路行列を見る方法は発見的方法としては使えるので、無意味になるわけではありません。

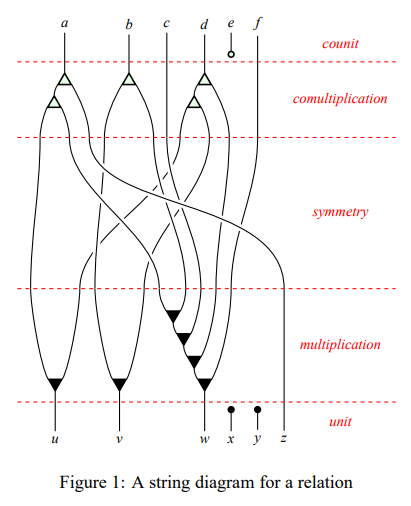
次の論文は、掲載されている絵（すぐ下）がそれっぽいので、なんかのヒントになるかも知れません（ちゃんと読まないとなんとも言えませんが）。

[WW15-]
Title: PROPs for Linear Systems
Authors: Simon Wadsley, Nick Woods
Submitted: 30 Apr 2015
Pages: 11p
URL: https://arxiv.org/abs/1505.00048

修正ミックス操作

「環境付き計算と依存アクテゴリー 1/n // 環境付き計算ペアのミックス操作」において、圏 $`\cat{E}`$ の射 $`(f_1, f_2)`$ に対して $`\mrm{Mix}( (f_1, f_2) ) = f_1\triangle f_2`$ を対応させる操作〈演算〉を定義しました。それは次の絵で表現できます。

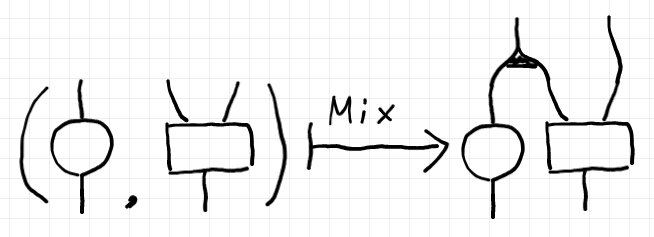
ミックスとよく似ているがわずかに違う操作として修正ミックス〈modified mix〉を次のように定義します。

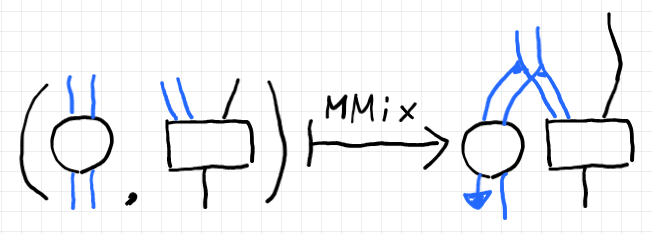
青い部分がミックスとの違いです。修正ミックスでは第一成分〈ベースパート〉の域・余域が直積の形をしている必要があります。そして、第一成分の出力の一部を捨てます。テキストで書いたほうがハッキリするでしょう（うざくなるけど）。

$`\text{For } g_1 : S_1 \times S_2 \to T_1 \times T_2 \In \cat{C}\\
\text{For } g_2 : (S_1 \times S_2)\times A \to B \In \cat{C}\\
\text{For }(g_1, g_2) : ( (S_1\times S_2)\times)A \to B \In \cat{E}\\
\quad \mrm{MMix}( (g_1, g_2) ) := (\Delta_{S_1\times S_2}\times \id_A ); (g_1 \times g_2) ; ( \pi^{S_1, S_2}_2 \times \id_B)
`$

ミックスは中置演算子記号 '$`\triangle`$' で表しましたが、$`\mrm{MMix}`$ は中置演算子記号 '$`\square`$' で表すことにします。

$`\quad g_1 \square g_2 := \mrm{MMix}( (g_1, g_2) ) \; : (S_1\times S_2)\times A \to S_2 \times B \In \cat{C}`$

修正ミックスは、最終的には不要になる（次節参照）のですが、カップリングの定義を模索するときに使ったので、ここに記しておきます。

環境付き計算ペアのカップリング

圏 $`\cat{E}`$ の射は、環境付き計算ペアで次のように表示できました。

$`\quad (f_1, f_2) : (S, A) \to (T, B)\In \cat{E}\\
\text{Where}\\
\quad f_1 : S \to T \In \cat{C}\\
\quad f_2 : (S\times)A \to B \In \cat{E}_{@S} = \cat{C}_{(S\times)}
`$

$`(S\times)`$ は注釈として入れているので、$`f_2 : A \to B \In \cat{E}_{@S}`$ でも同じことです。

この環境付き計算ペアを図示するとき次のように描くことにします。

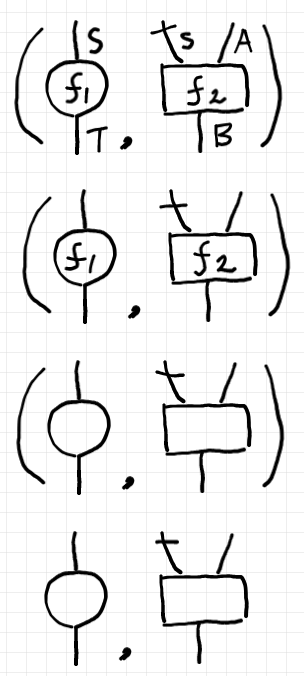
$`f_2`$ の左上のワイヤーに付いている横棒は、状態を表す目印です。$`f_2`$ の入力ワイヤーが3本以上になると、どこまでが状態か分かりにくくなるのでこの印を使うことにしました。混乱の心配がないなら横棒はなくてもいいです。上図、下に行くほど情報を省略しています。ワイヤーやノードにラベルがなくてもだいたい計算はできます。

$`(f_1, f_2)`$ と $`(g_1, g_2)`$ が圏 $`\cat{E}`$ の射、つまり環境付き計算ペアだとして、これらのカップリング〈coupling〉を定義しましょう。カップリングは、二重圏のプロ射／二重射のプロ方向への結合となる演算です。

カップリングに対する図式順中置演算子記号は '$`\coupl`$' とします。

$`\quad f \coupl g = (f_1, f_2)\coupl (g_1, g_2) = \mrm{Coupl}( (f_1, f_2), (g_1, g_2) )`$

カップリングは任意の2つの射 $`f, g`$ に対して定義できるわけではありません。カップリング可能な条件は以下のようです。

$`\quad f_1 \triangle f_2 = g_1`$

あるいは：

$`\quad \mrm{Mix}(f) = \mrm{Proj}(g)`$

そして、カップリングの定義は以下のとおりです。

$`\quad (f_1, f_2)\coupl (g_1, g_2) := (f_1, g_1\square g_2) = (f_1, (f1\triangle f2)\square g_1)
`$

この定義は、僕が最初に思い付いた定義です。修正ミックス $`\square`$ を使ってます。が、少し計算すると、もっと直接的な形に書けます。ファイバーパート $`(f1\triangle f2)\square g_1`$ を計算してみます。

$`f`$ を紫色、$`g`$ をピンクで描きます。下段の等式から、$`(f_1\triangle f_2)\square g_2`$ は結局、$`f_1`$ とは無関係で $`f_2, g_2`$ から計算できることが分かります。

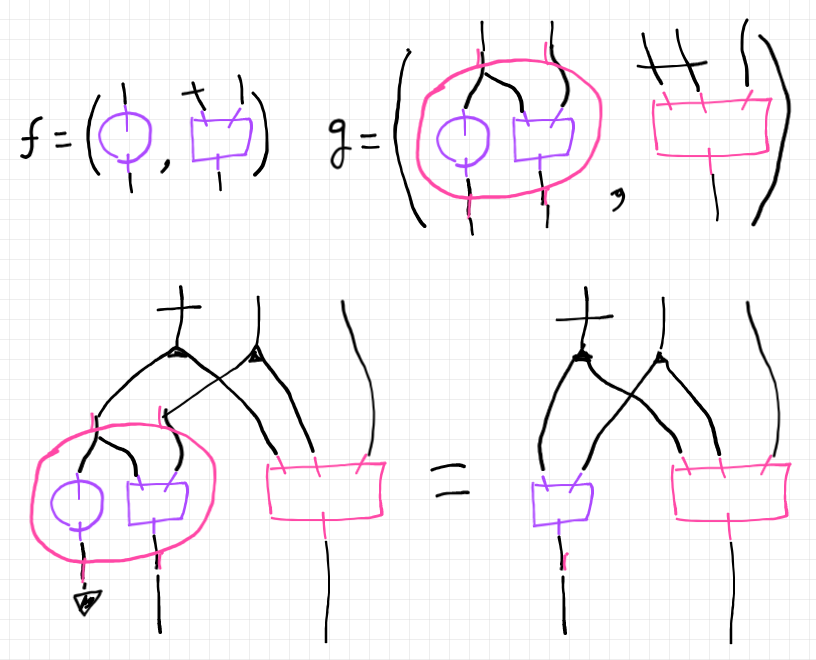
演算子記号 '$`\coupl`$' をオーバーロード〈多義的使用〉して、次のように定義します。

$`\quad f_2 \coupl g_2 := (\Delta_{S\times A} \times \id_B); (f_2 \times g_2)`$

すると、環境付き計算ペアのカップリングは次のように書き直せます。

$`\quad (f_1, f_2)\coupl (g_1, g_2) := (f_1, f_2 \coupl g_2)`$

オーバーロードしているので、左辺の $`\coupl`$ は環境付き計算ペアの演算、右辺の $`\coupl`$ はファイバーパートの演算です。

上の図が示唆するように、カップリングのプロファイル（域・余域の仕様）は次のようになります。

$`\text{For }(f_1, f_2) : (S, A) \to (T, B) \In \cat{E}\\
\text{For }(g_1, g_2) : (S\times A, C ) \to (T\times B, D) \In \cat{E}\\
\quad (f_1, f_2)\coupl (g_1, g_2) : (S, A\times C) \to (T, B \times D) \In \cat{E}`$

$`\triangle`$ の場合と同様に、$`\cat{E}`$ の対象に対しても $`\coupl = \mrm{Coupl}`$ を定義しておきます。

$`\quad (S, A) \coupl (S\times A, C ) := (S, A\times C)`$

$`\coupl`$ を $`\cat{E}`$ の対象に制限すると、次のような写像になります（ファイバー積の書き方については「ファイバーの計算の動機としてのプルバック公式 // プルバックってなに？」参照）。

$`\quad (\coupl) : |\cat{E}| \NFProd{\mrm{Mix}}{|\cat{C}|}{\mrm{Proj}} |\cat{E}| \to |\cat{E}| \In {\bf SET}`$

$`|\cat{E}| = |\cat{C}|\times |\cat{C}|`$ だったので、

$`\quad (\coupl) : (|\cat{C}| \times |\cat{C}|) \NFProd{(\times)}{|\cat{C}|}{\pi_1} (|\cat{C}|\times |\cat{C}|) \to |\cat{C}|\times |\cat{C}| \In {\bf SET}`$

$`\cat{E}`$ の対象に制限した $`(\coupl)`$ の計算はとても簡単なので、チェックサム（単純な検算）として使えます。

ところで、このカップリングという演算はどこから出てきたのでしょう？いきなり定義を出されると唐突な感じでしょう。多少の試行錯誤はしましたが、「環境付き計算ペア達の全体が依存アクテゴリーを形成する」と想定して、「だったら、こうなるはずだ」と推測していくと（ある意味“自然に”）この定義に辿り着きます。中間段階で修正ミックス $`(\square)`$ を使いましたが結局不要だったのは、試行錯誤のなごりです。

演算達が出揃った

ここまでで、次のような演算〈関手〉達が定義できました。

ファイブレーションの射影 $`\mrm{Proj}: \cat{E} \to \cat{C}`$
ミックス $`\mrm{Mix}: \cat{E} \to \cat{C}`$
自明持ち上げ $`\mrm{TLift} : \cat{C} \to \cat{E}`$
カップリング $`\mrm{Coupl} : \cat{E} \NFProd{\mrm{Mix}}{\cat{C}}{\mrm{Proj}} \cat{E} \to \cat{E}`$

これらを絵で描けば次のとおりです。

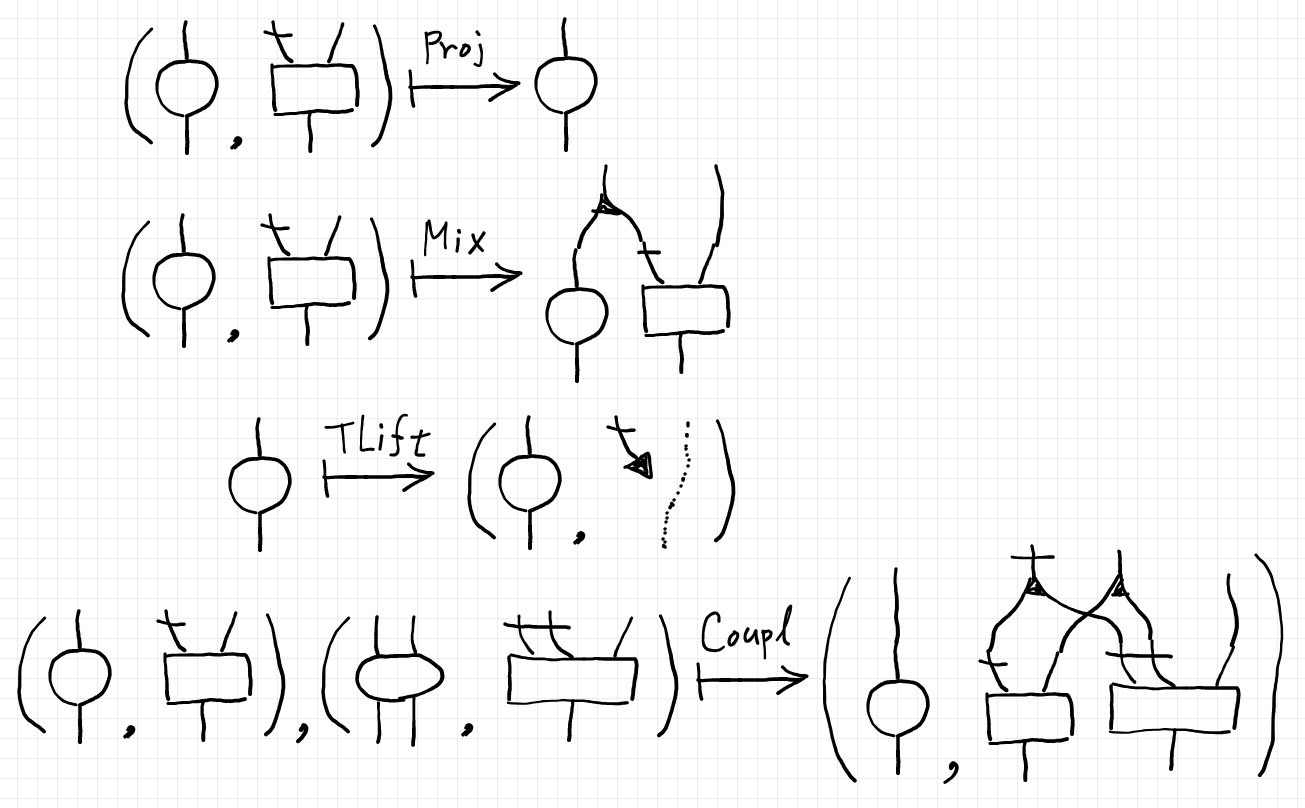
あとは、これらの演算達が二重圏を形成することを確認すれば、環境付き計算ペア達の全体は依存アクテゴリーとなります。より具体的に言えば：

ファイブレーションの射影 $`\mrm{Proj}: \cat{E} \to \cat{C}`$ は、プロ射／二重射の域〈ソース〉を与える。
ミックス $`\mrm{Mix}: \cat{E} \to \cat{C}`$ は、プロ射／二重射の余域〈ターゲット〉を与える。
自明持ち上げ $`\mrm{TLift} : \cat{C} \to \cat{E}`$ は、タイト射に対する恒等二重射を与える。
カップリング $`\mrm{Coupl} : \cat{E} \NFProd{\mrm{Mix}}{\cat{C}}{\mrm{Proj}} \cat{E} \to \cat{E}`$ は、プロ射／二重射のプロ方向への結合〈プロ結合 | 外部結合〉を与える。

実際の確認は次の記事にします。

続きは環境付き計算と依存アクテゴリー 3/n