圏論的レンズ 4：テレオロジー圏 - 檜山正幸のキマイラ飼育記 (はてなBlog)

$\newcommand{\cat}[1]{\mathcal{#1} } \newcommand{\op}{\mathrm{op}} \newcommand{\id}{\mathrm{id}} \newcommand{\In}{\text{ in }} \newcommand{\lact}{\mathop{\bullet} } \require{color} \newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }% \newcommand{\Where}{\Keyword{Where } }%$ レンズ／オプティックを記述する道具としてテレオロジー圏が便利そうです。紹介しておきます。

内容：

参考文献
アクテゴリー〈加群圏〉
テレオロジー圏とストリング図
テレオロジー圏の定義

最初の記事＋シリーズ目次

参考文献

テレオロジー圏〈teleological category〉は、次で論文でヘッジズによって導入されました。

Title: Coherence for lenses and open games
Author: Jules Hedges
Submitted: 15 Sep 2017 (v3)
Pages: 30p
URL: https://arxiv.org/abs/1704.02230

ライリーの論文でも説明されています。

Title: Categories of Optics
Author: Mitchell Riley
Submitted: 7 Sep 2018 (v2)
Pages: 51p
URL: https://arxiv.org/abs/1809.00738

ロマンは、ヘッジズのオリジナルとはだいぶ違った形の定義を提案しています。

Title: Composing optics
Author: Mario Roman
Date: February 6, 2020
Pages: 21p
URL: https://www.ioc.ee/~mroman/data/notes/composingoptics.pdf

ヘッジズ論文の"5.1. Definition."で定義されたテレオロジー圏は、対称モノイド圏に“ある種の双対性構造”を付加したものです。一方、ロマン論文"Definition 12."のテレオロジー圏は、アクテゴリー〈加群圏〉のペアを拡張した圏です。どうやら同値らしいですが、初見の印象はだいぶ違います。

この記事では、ロマンのテレオロジー圏を紹介します -- より一般的で使い勝手が良さそうだからです。

アクテゴリー〈加群圏〉

加群圏〈module category〉とは、モノイド圏 $\cat{M}$ が左または右から作用する圏 $\cat{C}$ のことです。 $\cat{M}, \cat{C}$ が小さい場合なら、双関手〈二項関手〉

$\quad L:\cat{M}\times \cat{C} \to \cat{C} \In {\bf Cat}$

により左モノイド作用〈left monoidal action〉が定義されます。双関手をカリー化すれば：

$\quad L^\cap:\cat{M} \to [\cat{C}, \cat{C}] \In {\bf Cat}$

ここで、 $[\cat{C}, \cat{C}]$ は自己関手達の関手圏（射は自然変換）です。 $L$ の代わりに $L^\cap$ を使う場合も多いです。以下では、左モノイド作用 $L$ を中置演算子記号 ' $\bullet$ ' で表します*1。

加群圏に関する過去記事には次があります。

加群圏をアクテゴリー〈actegory〉とも呼びます。レンズ／オプティックの界隈だと、アクテゴリーと呼ぶほうが多数派のようです。nLab項目に "actegory" があります。

https://ncatlab.org/nlab/show/actegory

テレオロジー圏とストリング図

現在、オプティックと呼ばれるモノは矢鱈にたくさんあります。同じ種類のオプティック達は圏を形成するので、オプティックの圏〈category of optics〉が矢鱈にたくさんあると言っても同じです。たくさんあるオプティックの圏の共通構造を抜き出して抽象化したドクトリン（「圏論的ドクトリンの安直な導入」参照）がテレオロジー圏です*2。

テレオロジー圏は抽象的ですが、テレオロジー圏のなかでの計算はストリング図で遂行できます。若干語弊があるかも知れませんが；「圏論的レンズ 3：レンズ／オプティックのための描画法」で述べたような絵による記述・計算がスムーズに出来る圏がテレオロジー圏だ、と言ってもいいでしょう。絵を描けるという点では、テレオロジー圏は具体的で手で触れる側面も持ちます。

圏 $\cat{C}$ の射を単方向データ変換子〈unidirectional data transformer〉と考えましょう。 $\cat{C}$ から双方向データ変換子〈bidirectional data transformer〉を作り出す最も簡単な方法は $\cat{C}\times \cat{C}^\op$ を作ることです。 $\cat{C}\times \cat{C}^\op$ の射 $(f, g)$ は次のように図示されます。

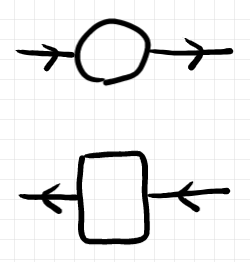
左から右の順方向に走る $f$ （丸）と右から左の逆方向に走る $g$ （四角）を単にペアにしただけです。

$\cat{C}$ には $\cat{M}$ が左から作用する（つまり左アクテゴリー＝左加群圏）としましょう*3。わかりにくいなら、 $\cat{M} = \cat{C}$ で、左作用は左からのモノイド積掛け算と思ってもかまいません。左作用があれば次のような射を考えることができます。

$f:A \to M\lact B \In \cat{C}$
$g:M\lact Y \to X \In \cat{C}$

$\cat{M}$ の対象は水色で描くと次のようになります。反時計回り規約（「圏論的レンズ 3：レンズ／オプティックのための描画法」参照）により、結合の方向が左から右なら、モノイド作用の左因子（ $\cat{M}$ の対象）が下に配置されます。逆方向の右から左に対しては左因子が上です。

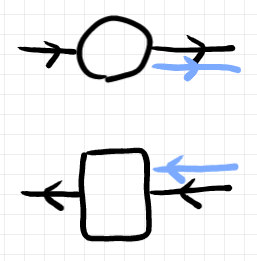
上の図は、残余出力（水色右向きワイヤー）を持つ順行パートと残余入力（水色左向きワイヤー）を持つ逆行パートのペアとみなせます。水色のワイヤーをカーブさせれば、双方向データ変換子内部のプライベートチャンネルが出来上がります。

さて、ワイヤーベンディング〈曲げ〉の部分を単独の射と考えましょう。次の図のオレンジ色の点線の右の部分がワイヤーベンディングを射と考えたものです。この射を同語反復射〈tautological morphism〉またはテレオロジー射〈teleological morphism〉と呼びます。

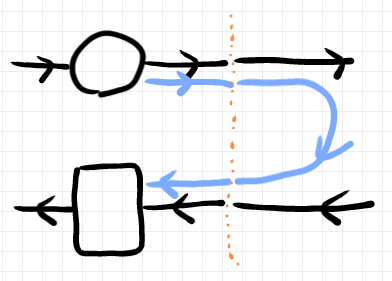
同語反復射を以下の右辺のようにも描くことにします。

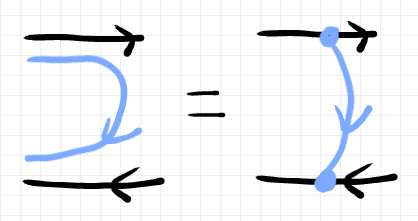
水色ワイヤーを省略しないで、左辺のように描くほうがわかりやすいと思うのですが、次節で紹介するロマンの描画法が右辺です。

テレオロジー圏の定義

ロマン論文に沿ってテレオロジー圏〈teleological category〉の定義を述べていきます。ただし、一部ライリーの用語・記法・定義も混ぜます。

テレオロジー圏の構成素は次のものです。

モノイド圏 $\cat{M} = (\cat{M}, \otimes, I, \alpha, \lambda, \rho)$
圏 $\cat{C}$
左モノイド作用 $(\bullet):\cat{M} \times \cat{C} \to \cat{C}$
圏 $\cat{T}$
関手 $\iota: \cat{C}\times \cat{C}^\op \to \cat{T}$
同語反復射の族 $t_{M, A, B}\in \mathrm{Mor}(\cat{T}) \:\text{ for }M\in |\cat{M}|, A, B \in |\cat{C}|$

圏 $\cat{T}$ の対象類は：

$\quad |\cat{T}| = |\cat{C}\times \cat{C}^\op| = |\cat{C}|\times |\cat{C}|$

関手 $\iota$ は対象上で恒等〈identity-on-objects〉な関手です。 $\iota(f, g) = \iota( (f, g))$ をストリング図に描くときは $(f, g)\in \mathrm{Mor}(\cat{C}\times \cat{C}^\op)$ と同じ絵にします。なお、 $\iota$ はライリーの記法です。ロマンは無名の関手 $\cat{C}^\op \times \cat{C} \to \cat{T}$ を使っています（どっちでもいいけど）。

前節で述べた描画法により、同語反復射

$\quad t_{M, A, B} : (M\lact A, M\lact B) \to (A, B) \In \cat{T}$

は、次のように描きます（ロマン論文 p.15 からコピー）。

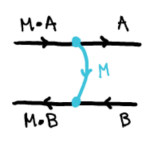
同語反復射には次の4つの公理〈法則〉を要求します（ロマン論文 p.15 からコピー）。

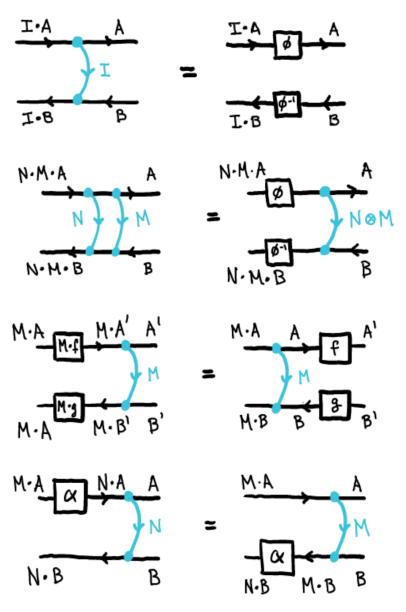
図のなかのラベルがオーバーロードされて（同じ文字が違う意味で使われて）いてわかりにくいですね。3番目の等式の左辺下側のラベル $M\lact A$ は $M\lact B$ の間違いです。オーバーロード解決やミス修正の良い練習問題だとも言えますが、補足説明しましょう*4。

1番目の等式の $\phi$ と2番目の等式の $\phi$ は別物で、それぞれ左モノイド作用の左単位律子〈left unitor〉と結合律子〈associator〉です。右肩に添え字を付けて区別しましょう。

$\quad \phi^\lambda_A : I\lact A \to A \In \cat{C}\\ \quad \phi^\alpha_{M, N, A} : M\lact (N\lact A) \to (M\otimes N)\lact A \In \cat{C}$

4番目の等式の $\alpha$ は、左辺と右辺で別物です。適当な $a:M \to N \In \cat{M}$ に対して次のように定義されます。

$\quad \alpha_A := a\lact A = a\lact \id_A : M\lact A \to N\lact A \In \cat{C}\\ \quad \alpha_B := a\lact B = a\lact \id_B : M\lact B \to N\lact B \In \cat{C}$

対象と恒等射を同一視して、次のような書き方もします。

$\quad M\lact f = \id_M \lact f\\ \quad a\lact A = a \lact \id_A$

以上のような約束で、4つの等式をテキストに書き下すと以下のようになります。

$\quad t_{I, A, B} = \iota(\phi^\lambda_A, (\phi^\lambda_B)^{-1} )\\ \qquad : (I\lact A, I\lact B) \to (A, B) \In \cat{T}\\ \:\\ \quad t_{N, M\lact A, M\lact B} ; t_{M, A, B} = \iota(\phi^\alpha_{N, M, A}, (\phi^\alpha_{N, M, B})^{-1} ); t_{N\otimes M, A, B} \\ \qquad : (N\lact M\lact A, N\lact M\lact B) \to (A, B) \In \cat{T}\\ \:\\ \quad \iota(\id_M\lact f, \id_M\lact g) ; t_{M, A', B'} = t_{M, A, B};\iota(f, g)\\ \qquad : (M\lact A, M\lact B) \to (A', B') \In \cat{T}\\ \quad \Where f:A \to A', g:B' \to B \In \cat{C}\\ \:\\ \quad \iota(a\lact \id_A, \id_{N\lact B}) ; t_{N, A, B} = \iota(\id_{M\lact A}, a\lact \id_B); t_{M, A, B} \qquad : (M\lact A, N\lact B) \to (A, B) \In \cat{T}\\ \quad \Where a : M \to N \In \cat{M}$

いつものことですが、テキストで表すと煩雑でワケわからなくなってしまいます。しかし一方、絵の曖昧杜撰〈あいまいずさん〉な部分をテキストの精密な情報が補ってくれます。絵とテキストは相補的なツールなのです。

さてところで、これらの等式は、具象オプティック＝具象レンズの場合を思い起こせば自然なものに思えるでしょう。逆に、これらの法則が成り立っているなら、具象オプティックの圏と同様なストリング図計算が可能になります。テレオロジー圏は、具象オプティックの圏の素直な抽象化と言えます。

*1:左モノイド作用には、双関手だけではなくて、作用の結合律や単位律に関する律子（associator, unitor）も含まれます。

*2:すべてのレンズ／オプティックの圏がテレオロジー圏でカバーできるわけではありません。

*3:左作用と右作用を区別しない記述も見受けますが、ハッキリと区別・意識しましょう。

*4:僕の補足説明に相当することは、ロマンの論文にはまったく書いてありません。この論文はドラフトで省略が多いのですが、この程度の補完は必要になることがあります。