グリッド計算とコーナリング、そして二重圏

ここ最近、テレオロジー圏、コンパクト閉圏、トレース付きモノイド圏などのあいだの親族的関連性に興味を持っています。なんか資料がないかな、と探していたら次の論文を見つけました。

• Title: Cornering Optics
• Authors: Guillaume Boisseau, Chad Nester, Mario Roman
• Submitted: 2 May 2022
• Pages: 14p
• URL: https://arxiv.org/abs/2205.00842

コレ、おもしろーい。実用上も役に立ちそう。

ボアッソ*1／ネステル*2／ロマンは、与えられたモノイド圏から二重圏を作る自由コーナリング構成〈free cornering construction〉を導入しています。これの直接の目的は、オプティックに対して新しい定式化を与えることですが、もっと広くモデリングと計算の手法として使えそうです*3。$`\newcommand{\cat}[1]{\mathcal{#1} }
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\mrmo}[1]{\overline{\mathrm{#1}} }
\newcommand{\In}{\text{ in }}
\newcommand{\ot}{\leftarrow }
\newcommand{\conc}{\mathop{\#} }
\newcommand{\dblto}[2]{ \overset{#1}{\underset{#2}{\Longrightarrow}} }
\newcommand{\id}{\mrm{id}}
\newcommand{\pass}{\mrm{pass}}
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
\newcommand{\When}{\Keyword{When } }%
\newcommand{\Then}{\Keyword{Then } }%
`$

内容：

はじめに

ボアッソ／ネステル／ロマンが使っている道具は二重圏です。なので、最初に二重圏の紹介をします。しかし、実際に使う二重圏は特殊なもの（単一対象二重圏）なので、二重圏の一般論はさほど必要としません。むしろ、二重圏の一般論と特殊な二重圏（とその図示）のあいだの関係が錯綜していて混乱するかも知れません。

引き続く2節を飛ばして、「グリッド図」の節から読むほうが混乱を避けられるでしょう。グリッド図とグリッド計算が何であるかを理解した後で、二重圏の一般論との関係をゆっくり考える（あるいはヤッパリ考えない）のでもいいと思います。

二重圏

二重圏〈double category〉は2次元の圏ですが、1次元の射が縦方向と横方向の二種類あります。2次元の射は、1次元の射による4辺で囲まれた矩形領域として表されます。二種類の1-射は縦射〈vertical morphism〉と横射〈horizontal morphism〉と呼びますが、（よくあることですが）困ったことに、縦横の選び方が人により違います。そのへんの事情は、次の論文の "1.3 Conventions and Notation" に書いてあります。

• Title: Discrete Double Fibrations
• Author: Michael Lambert
• Submitted: 17 Jan 2021
• Pages: 32p
• URL: https://arxiv.org/abs/2101.06734

僕も今まで「縦・横」を使ってきましたが、ここでは、パレ〈Robert Paré〉のチュートリアル資料 "Double Categories" に従って、「縦・横」を使わないで「内部〈internal〉」という形容詞を使う用語法にします*4。

二重圏は「“圏の圏”のなかの圏対象〈category object〉」です。この時点で既にややこしいのですが、次のような圏（“圏の圏”の対象）と関手（“圏の圏”の1-射）を考えます。上線を引いているのは、$`\cat{M}, \cat{O}`$ が備える $`\mrm{dom}, \mrm{cod}, \mrm{id}, \mrm{comp}`$ と区別するためです。

1. 圏 $`\cat{O} \in |{\bf CAT}|`$
2. 圏 $`\cat{M} \in |{\bf CAT}|`$
3. 関手 $`\mrmo{dom}: \cat{M} \to \cat{O} \In {\bf CAT}`$
4. 関手 $`\mrmo{cod}: \cat{M} \to \cat{O} \In {\bf CAT}`$
5. 関手 $`\mrmo{id}: \cat{O} \to \cat{M} \In {\bf CAT}`$
6. 関手 $`\mrmo{comp}: \cat{M}\times_{\cat{O}}\cat{M} \to \cat{M} \In {\bf CAT}`$

$`\cat{M}\times_{\cat{O}}\cat{M}`$ は、$`\mrmo{cod}, \mrmo{dom}`$ の余スパンから作った“圏のファイバー積”です。このたぐいのファイバー積は断りなしに $`\times_{\cat{O}}`$ を使って表します。

なお、今の文脈では、$`{\bf CAT}`$ の2-射〈自然変換〉は捨てて単なる圏〈1-圏〉と考えています。圏の公理を等式的に考えるので、2-射は不要です。1-圏としての“圏の圏”を $`{\bf CAT}|_{\le 1}`$ と書くと紛れがないですが、まー、いいとしましょう。

これらの素材〈構成素〉に対して、通常の圏の法則を要請した構造が二重圏です。例えば、結合の（図式順の）左単位法則なら次の可換図式を要請します。

$`\require{AMScd}
\quad
\begin{CD}
\cat{O}\times_{\cat{O}}\cat{M} @>{\mrm{Proj}^2}>> \cat{M}\\
@V{ \mrmo{id}\times_{\cat{O}}\mrm{Id}_{\cat{M}}}VV @|\\
\cat{M}\times_{\cat{O}}\cat{M} @>{\mrmo{comp}}>> \cat{M}
\end{CD}\\
\text{commutative in }{\bf CAT}
%`$

ここで、$`\mrm{Proj}^2`$ は、ファイバー積に関する第二射影です。$`\mrm{Id}_{-}`$ は圏 $`{\bf CAT}`$ が持っている恒等（恒等関手を作る操作）です。ちなみに、二重圏にかかわる“恒等”はたくさんあります。

1. $`\mrm{Id}`$ ： 圏 $`{\bf CAT}`$ の恒等 $`|{\bf CAT}| \to \mrm{Mor}({\bf CAT}) \In \mathbb{SET}`$
2. $`\mrmo{id}`$ ： 二重圏の恒等 $`\mrmo{id}: \cat{O} \to \cat{M} \In {\bf CAT}`$
3. $`\mrm{id}^{\cat{O}}`$ ： 圏 $`\cat{O}`$ の恒等 $`\mrm{id}^{\cat{O}}:|\cat{O}| \to \mrm{Mor}(\cat{O}) \In {\bf SET}`$
4. $`\mrm{id}^{\cat{M}}`$ ： 圏 $`\cat{M}`$ の恒等 $`\mrm{id}^{\cat{M}}:|\cat{M}| \to \mrm{Mor}(\cat{M}) \In {\bf SET}`$

さて、各種射／各種結合の、「縦・横」を使わない呼び名は次のようです。参考に、nLab項目の「縦・横」を記しておきます。

1. 二重圏の対象〈0-射〉 ： 圏 $`\cat{O}`$ の対象〈0-射〉
2. 二重圏の1-射 ： 圏 $`\cat{M}`$ の対象〈0-射〉、nLabの横射〈horizontal morphism〉、またはプロ射〈proarrow〉
3. 二重圏の1-射の結合 ： 関手 $`\mrmo{comp}`$ の対象〈0-射〉部分による結合、nLabの横結合〈horizontal composition〉
4. 二重圏の内部1-射 ： 圏 $`\cat{O}`$ の射〈1-射〉、nLabの縦射〈vertical morphism〉
5. 二重圏の内部1-射の内部結合 ： 写像 $`\mrm{comp}^{\cat{O}}`$ による結合、nLabの縦結合〈vertical composition〉
6. 二重圏の2-射 ： 圏 $`\cat{M}`$ の射〈1-射〉
7. 二重圏の2-射の結合 ： 関手 $`\mrmo{comp}`$ の射〈1-射〉部分による結合、nLabの横結合〈horizontal composition〉
8. 二重圏の2-射の内部結合 ： 写像 $`\mrm{comp}^{\cat{M}}`$ による結合、nLabの縦結合〈vertical composition〉

1-射と内部1-射を「縦・横」どちらの方向に割り当てるかは人によりけりですが、パレとnLabは揃っているようです（下の図）。パレとnLabが使っている文字と、後でこの記事内で後で使う文字も併記します。矢印はペースティング図（ストリング図ではない）における描画方向です。

射の種類	パレ	nLab	この記事
0-射	ラテン大文字	ラテン小文字（後方）	(不要)
1-射	ラテン小文字 →	ラテン小文字 →	ギリシャ大文字 ↓
内部1-射	ラテン小文字（後方）↓	ギリシャ小文字 ↓	ラテン大文字 →
2-射	ギリシャ小文字 ↓	ギリシャ小文字（後方）↓	ギリシャ小文字 →

パレの図：

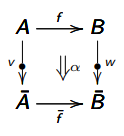
nLabの図：

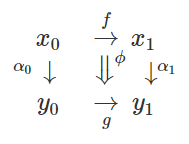
シュルマン〈Mike Shulman〉も、パレ／nLabと同じ描画方向を使っています。

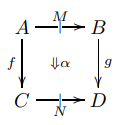
パレは縦矢印に黒丸を付けてましたが、シュルマンは横矢印に縦棒を付けています。またシュルマンは、この描画方向を用語法にも反映させて、$`\mrmo{dom}(\alpha)`$ を $`\alpha`$ の左フレーム〈left frame〉、$`\mrmo{cod}(\alpha)`$ を $`\alpha`$ の右フレーム〈right frame〉と呼んでいます。$`\alpha`$ の域・余域（またはソース／ターゲット）は $`\mrm{dom}^{\cat{M}}(\alpha), \mrm{cod}^{\cat{M}}(\alpha)`$ （図では上端／下端）のほうを（シュルマン流では）指します。

ボアッソ／ネステル／ロマンの二重圏

悪いニュースがあります。ボアッソ／ネステル／ロマンの描画方向は、パレ／nLab／シュルマンとは違っています。ボアッソ／ネステル／ロマンの縦射はパレ／nLab／シュルマンの横射〈プロ射〉です。さらに、描画法はペースティング図ではなくてストリング図を使うので、縦射は横向きワイヤーになります。「縦エッジ〈vertical edge〉」とか言われると、何を意味するのかワカリマセン。

「Int構成〈GoI構成〉 再論」より：

このテの話だと、順番や向きの決め方はややこしくなります。抽象的・形式的には同じ定義でも、上下左右の約束や描画法のバリエーションは色々と生じます。

まさに、たいへんややこしい事態になっています。

こうしましょう； ボアッソ／ネステル／ロマンが扱っている二重圏はかなり特殊な二重圏です。また、ペースティング図はまったく使ってなくてストリング図だけです。二重圏の一般論との対応はあまり気にしないで、特殊な二重圏をストリング図で表すことに集中しましょう。

ただし、二重圏の射をストリング図で表すことはボアッソ／ネステル／ロマンに特有な手法ではありません。nLabにあったストリング図をペースティング図（再掲）と共に並べておきます。「縦射は横向きワイヤーになる」ことは、これを見れば分かるでしょう。

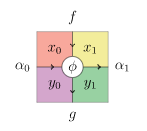
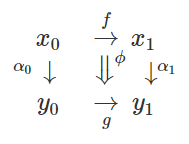
二重圏（とイクイップメント）のストリング図については、メイヤーの丁寧な解説があります。

• Title: String Diagrams For Double Categories and Equipments
• Author: David Jaz Myers
• Submitted: 8 Dec 2016 (v1), 2 Mar 2018 (v4)
• Pages: 33p
• URL: https://arxiv.org/abs/1612.02762

二重圏の2-射をペースティング図で表した場合、それをタイル〈tile〉と呼ぶことがあります。縦横の結合〈composition〉によりタイルを並べます。一方、ストリング図を使うと、2-射はグリッドのノードになります。ワイヤーを縦横に繋いでグリッド状図形を構成します。ストリング図を使った二重圏の計算はグリッド計算〈grid calculus〉と呼べるでしょう。

グリッド図

上下左右方向に“ワイヤーの四本脚”を持つノードを幾つか、グリッド状に配置した図形（一種のストリング図）をグリッド図〈grid diagram〉と呼ぶことにします。縦方向ワイヤーは上から下、横方向ワイヤーは左から右の向きを持ちます -- もちろん、ここでの恣意的な規約です。以下はグリッド図の例です。

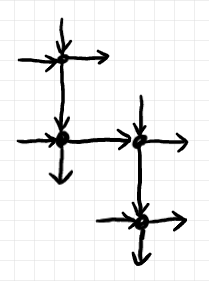
「図で横向きのワイヤーを縦射と呼び、別な人はそれを横射とも呼ぶ」というようなこんがらかった事情がありますが、今はそんな事情は無視して、上下左右は絵の見た目のまんまで語ることにします。

ノードは本来1次元図形〈点〉ですが、なかにラベルを書き込むために丸や四角で描くとことがあります。

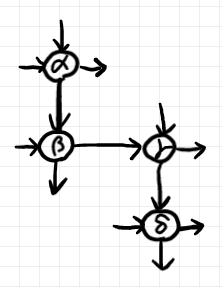
ノードとワイヤーにラベルを付けることができます。ラベルは個々のノード／ワイヤーを識別するためのIDラベルではなくて、型ラベルです。同じラベルを何度も使えます。以下は、ワイヤーにラベルを付けた例です。

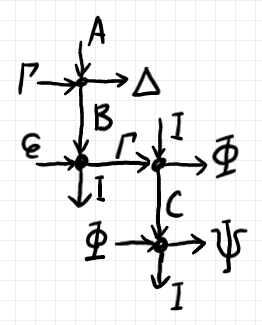
ここで、縦方向ワイヤーのラベル $`I`$ と、横方向ワイヤーのラベル $`\varepsilon`$ は特別扱いします。ラベル $`I, \varepsilon`$ が付けられたワイヤーは描かなくてよい、というルールを設けます。よって、上の絵は次のように描いても同じことです。

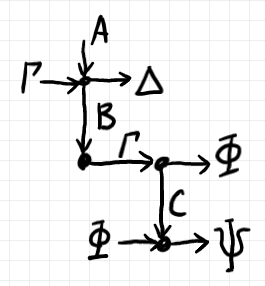
ノードのラベルも書き込むと次のようになります。

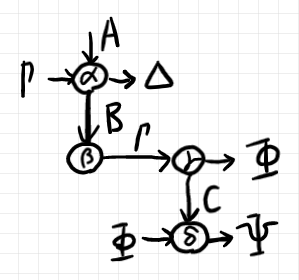
ノード／ワイヤーのラベルに使う文字の約束を表にしておきます。二重圏の解説を飛ばした人は「二重圏の射」は気にしなくていいです。

図形の次元	ラベルの文字	二重圏の射
0次元（点）	ギリシャ小文字 α など	2-射
縦方向1次元	ラテン大文字 A など	内部1-射
横方向1次元	ギリシャ大文字 Γ など	1-射
2次元（背景エリア）	（なし）	0-射〈対象〉

グリッド図のテキスト表示

毎回グリッド図を描くわけにもいかないので、グリッド図のテキスト表示〈テキスト・エンコード法〉を考えましょう。

まず単一のノードは次の形で書きます。

$`\quad \alpha :: \Gamma \dblto{A}{B} \Delta`$

ノードをワイヤーで繋ぐことを結合〈composition〉と考えて、結合の図式順演算子記号を次のように決めます。

• 左右に並んだノードを横方向に結合する： 演算子記号 $`\otimes`$
• 上下に並んだノードを縦方向に結合する： 演算子記号 $`\conc`$

これらの演算子記号は、ワイヤーの演算としても使います。

• 左右に並んだ縦方向ワイヤーを横方向にまとめる： 演算子記号 $`\otimes`$
• 上下に並んだ横方向ワイヤーを縦方向にまとめる： 演算子記号 $`\conc`$

さらに、ワイヤーをノードとみなす演算が必要です。

• 縦方向ワイヤーをノードとみなす： $`\id`$
• 横方向ワイヤーをノードとみなす： $`\pass`$

では、実際にグリッド図をテキスト表示してみます。前節のグリッド図を、テキスト表示のために少しレイアウト調整したものが次です。

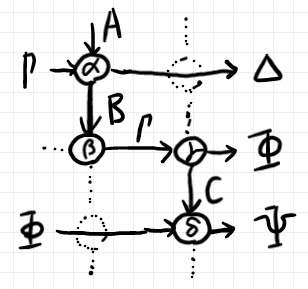
左上のノードのグリッド座標を (1, 1) として、各グリッド座標位置に存在するノードを書き出してみます。

1. (1, 1) ： $`\alpha :: \Gamma \dblto{A}{B} \Delta`$
2. (1, 2) ： $`\pass_\Delta :: \Delta \dblto{I}{I} \Delta`$
3. (2, 1) ： $`\beta :: \varepsilon \dblto{B}{I} \Gamma`$
4. (2, 2) ： $`\gamma :: \Gamma \dblto{I}{C} \Phi`$
5. (3, 1) ： $`\pass_\Phi :: \Phi \dblto{I}{I} \Phi`$
6. (3, 2) ： $`\delta :: \Phi \dblto{C}{I} \Psi`$

横方向の結合を演算子記号 $`\otimes`$ で表して、縦方向はそのまま縦に配置した形は：

$`\quad
\begin{matrix}
\alpha \otimes \pass_\Delta\\
\beta \otimes \gamma \\
\pass_\Phi \otimes \delta
\end{matrix}`$

縦の配置を演算子記号 $`\conc`$ を使ってシリアライズすると：

$`\quad
(\alpha \otimes \pass_\Delta) \conc
(\beta \otimes \gamma) \conc
(\pass_\Phi \otimes \delta)
%`$

これを単一のノードとみなしてプロファイルも書き出すと：

$`\quad
(\alpha \otimes \pass_\Delta) \conc
(\beta \otimes \gamma) \conc
(\pass_\Phi \otimes \delta)
:: \Gamma\conc \varepsilon\conc \Phi \dblto{A\otimes I}{I\otimes I} \Delta\conc \Phi\conc \Psi
%`$

ここで、$`I, \varepsilon`$ が演算 $`\otimes, \conc`$ の単位元だと仮定すると：

• $`\Gamma\conc \varepsilon\conc \Phi = \Gamma\conc \Phi`$
• $`A\otimes I = A`$
• $`I\otimes I = I`$

これを使って書き換えましょう。

$`\quad
(\alpha \otimes \pass_\Delta) \conc
(\beta \otimes \gamma) \conc
(\pass_\Phi \otimes \delta)
:: \Gamma\conc \Phi \dblto{A}{I} \Delta\conc \Phi\conc \Psi
%`$

$`\pass_\Delta, \pass_\Phi`$ を $`\Delta, \Phi`$ とオーバーロードする書き方で簡略化するともっと短くなります。

$`\quad
(\alpha \otimes \Delta) \conc
(\beta \otimes \gamma) \conc
(\Phi \otimes \delta)
:: \Gamma\conc \Phi \dblto{A}{I} \Delta\conc \Phi\conc \Psi
%`$

グリッド図を自由・手軽に描けるツール／環境はないので、致し方ないので、グリッド図の伝達のためにはテキストにシリアライズした形式を使います。

モノイド圏によるラベリング

今まで、ワイヤーのラベルは単なる文字として扱ってきました。ここから先では、ワイヤーのラベルは実体を持つと考えます。

$`\cat{C} = (\cat{C}, \otimes, I)`$ を厳密モノイド圏とします。一般に、モノイド圏は厳密とは限りませんが、モノイド圏の厳密化定理により厳密化できます。$`\cat{C}`$ は厳密化した後のモノイド圏と考えてください。

$`\cat{C}`$ の射はデータ型だと考えると、話を理解しやすいと思います。$`\cat{C}`$ の射を $`A, B`$ などで書きます。グリッド図のラベルとして出てきた $`A, B`$ などは $`\cat{C}`$ の対象（気持ちとしてはデータ型）だったとします。特殊なラベル $`I`$ の実体はモノイド単位で、演算子記号 $`\otimes`$ はモノイド積を表すものだったのです。これで、縦方向のワイヤーは $`\cat{C}`$ の対象を表し、縦方向のワイヤーを横に並べることは $`\cat{C}`$ のモノイド積を意味していることが分かりました。

横方向のワイヤーに付けるラベル $`\Gamma, \Delta`$ などの意味は少し複雑です。まず、モノイド圏 $`\cat{C}`$ の対象に極性〈polarity〉を付けます。極性とは、二値の値です。$`\{+, -\}, \{\top, \bot\}, \{0, 1\}, \{\circ, \bullet\}`$ など、二値なら何でもいいのですが、ここでは $`\{\to, \ot \}`$ を使います。極性付きの対象の集合を $`|\cat{C}|\times \{\to, \ot\}`$ として、その要素を次のように書きます。

• 順行対象〈forward object〉： $`A^\to := (A, \to) \in |\cat{C}|\times \{\to, \ot\}`$
• 逆行対象〈backward object〉： $`A^\ot := (A, \ot) \in |\cat{C}|\times \{\to, \ot\}`$

順行対象／逆行対象は、非形式的に〈メンタルに〉次のように解釈します； 双方向通信を考えることにして、順方向の通信（例えばリクエスト）に使うデータ型 $`A`$ を（方向も込めて） $`A^\to`$ とします。同じデータ型 $`A`$ でも逆方向の通信（例えばレスポンス）に使うなら $`A^\ot`$ と書きます。

極性付き対象（順行対象と逆行対象）の集合 $`|\cat{C}|\times \{\to, \ot\}`$ から作ったリストの集合を $`\mrm{List}(|\cat{C}|\times \{\to, \ot\})`$ とします。大文字ギリシャ文字は $`\mrm{List}(|\cat{C}|\times \{\to, \ot\})`$ の要素だったと解釈します。

$`\quad \Gamma, \Delta, \Phi, \Psi \in \mrm{List}(|\cat{C}|\times \{\to, \ot\})`$

特に、$`\varepsilon`$ は空リストのことでした。横方向のワイヤーを縦方向にまとめる演算子記号 $`\conc`$ の意味はリストの連接演算と解釈します。

極性付き対象のリストは次のようにブラケットで囲って表すことにします。（絵と合わせるには縦に並べるといいですが、横並びに書きます。）

$`\When\\
\quad \Gamma = [A^\to, C^\ot, C^\to, B^\ot]\\
\quad \varepsilon = [\,]\\
\quad \Phi = [A^\to]\\
\Then\\
\quad \Gamma\conc \varepsilon \conc \Phi \\
= [A^\to, C^\ot, C^\to, B^\ot]\conc[\,]\conc[A^\to] \\
= [A^\to, C^\ot, C^\to, B^\ot, A^\to]
`$

極性付き対象のリストは、簡単ならがらも、双方向通信のプロトコル（対話の約束）を表すと解釈できます。つまり、横方向のワイヤーは、双方向通信プロトコルでラベルされていたことになります。

処理ノードとコーナー・ノード

グリッド図のワイヤーの意味はハッキリしましたが、ノード（あるいはボックス）の意味は不明です。ノード達は、生成系〈system of generators | generating system〉と関係〈relations〉により定義します。二種類の生成ノード〈generating node〉があります。

• $`\cat{C}`$ の射 $`f:A \to B`$ に対して、グリッド図のノード $`\mrm{proc}(f) :: \varepsilon \dblto{A}{B} \varepsilon`$ がある。このタイプのノードを処理ノード〈processor node | processing node〉と呼ぶことにします。
• $`\cat{C}`$ の対象 $`A`$ に対して、以下の種類のグリッド図のノードがある。このタイプのノードをコーナー・ノード〈corner node〉と呼ぶことにします。
  1. receive from right コーナー： $`A\ulcorner :\varepsilon \dblto{I}{A} [A^\ot]`$
  2. receive from left コーナー： $` A\urcorner : [A^\to] \dblto{I}{A} \varepsilon`$
  3. send to right コーナー： $` A\llcorner :\varepsilon \dblto{A}{I} [A^\to]`$
  4. send to left コーナー： $` A\lrcorner : [A^\ot] \dblto{A}{I} \varepsilon`$

処理ノードは、$`\cat{C}`$ の射でラベルして示します。

コーナー・ノードは次のように図示します。

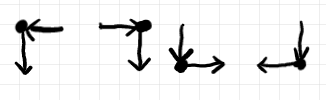
$`\cat{C}`$ における結合とモノイド積は、グリッド図の演算 $`\conc, \otimes`$ に移されます。

$`\For f, g \in \mrm{Mor}(\cat{C})\\
\quad \mrm{proc}(f ; g) = \mrm{proc}(f) \conc \mrm{proc}(g)\\
\quad \mrm{proc}(f\otimes g) = \mrm{proc}(f) \otimes \mrm{proc}(g)
`$

グリッド図の一般のノードは、$`\cat{C}`$ のすべての射に対する処理ノードと、$`\cat{C}`$ のすべての対象に対するコーナー・ノードをベースに、演算 $`\conc, \otimes`$ を使って組み合わせたものとして定義します。ただし、2つの組み合わせが実際には等しいことを主張する等式達（それが関係）も考慮します。

グリッド図の同値性を規定する等式達は今は述べませんが、それらは、ストリング図の自然な変形に対応します。

コーナリング

ここまで、グリッド図という視覚的表現を中心にして2次元計算の基礎を説明してきました。もっと抽象的な形で、厳密モノイド圏 $`\cat{C}`$ から二重圏を作る手続きを記述することもできます。この構成手続きを、ボアッソ／ネステル／ロマンは自由コーナリング構成〈free cornering construction〉と呼んでいます。

コーナリングとは、特殊な二重圏 -- 詳しく言えば、プロ射装備〈proarrow equipped〉単一対象二重圏を意味します。“厳密モノイド圏の圏”から、“コーナリング（特殊な二重圏）の圏”への自由生成関手が在るわけです。

「コーナリング」という言葉は、ワイヤーを90度曲げること（ワイヤー・コーナリング）も意味するので、ちょっと混乱しそうです。自由コーナリング構成で作られる圏論的構造は、コーナリング圏〈cornering category〉とか呼んだほうがよさそうな気がします。

二重圏ブームが来そう

グリッド図は、「左右の方向に双方向通信（または双方向変換）ができて、上下の方向には一方向のデータ処理ができるようなエージェントを表す」と解釈できます。ワイヤー・コーナリング（90度回転）があるので、左右から受け取った通信データを処理データに回したり、その逆に処理したデータを左右に送り出すことができます。

このような解釈ができるのは、左右と上下の二方向（比喩的には空間方向と時間方向）があるからです。モノイド圏でも結合方向とモノイド積方向がありますが、二重圏ではより柔軟な2次元計算ができます。二重圏って便利。

応用圏論〈Applied Category Theory | ACT〉の世界では、他にも二重圏を使った試みが見受けられるので、これから二重圏ブームが来るかも知れませんね。

追記： 象形文字記法

グリッド図のテキスト表示で、できるだけ図を連想できるように“象形文字”を考えてみます。$`\cat{C}`$ の対象 $`A`$ から決まるノード（二重圏の2-射）は、一律に $`A`$ を下付きで添えます。また、ある程度のオーバーロードを許すことにします。

• 縦の恒等 ：$`\id_A`$ 、単に $`A`$ でもよい。
• 横の恒等（順行） ：$`\pass_{[A^\to]} = \pass^\to_A`$ 、単に $`A^\to`$ でもよい。
• 横の恒等（逆行） ：$`\pass_{[A^\ot]} = \pass^\ot_A`$ 、単に $`A^\ot`$ でもよい。
• コーナー ： $`\llcorner_A, \lrcorner_A, \ulcorner_A, \urcorner_A `$
• 処理ノード ： $`\mrm{proc}(f)`$ 、単に $`f`$ でもよい。

組み合わせ：

• 左のベンディング ： $`\sqsubset_A := \ulcorner_A \conc \llcorner_A = \begin{pmatrix} \ulcorner_A \\ \llcorner_A \end{pmatrix} :: \varepsilon \dblto{I}{I} [A^\to, A^\ot]`$
• 右のベンディング ： $`\sqsupset_A = \urcorner_A \conc \lrcorner_A = \begin{pmatrix} \urcorner_A \\ \lrcorner_A \end{pmatrix} :: [A^\to, A^\ot] \dblto{I}{I} \varepsilon`$

モノイド圏 $`\cat{C}`$ の射
$`\quad f:S\otimes A \to S\otimes B \In \cat{C}`$
があるとき、これからプレオートマトンを作れます。$`A`$ を逆行入力、$`B`$ を順行出力とするプレオートマトンは次のように書けます。

$`\quad
\sqsubset_S \otimes
\begin{pmatrix}
\urcorner_S \otimes \ulcorner_A\\
f \\
\lrcorner_S \otimes \llcorner_B
\end{pmatrix}\\
=\;
\sqsubset_S \otimes
(
(\urcorner_S \otimes \ulcorner_A)\conc
f \conc
(\lrcorner_S \otimes \llcorner_B)
) :: \varepsilon \dblto{I}{I} [A^\ot, B^\to]
%`$

*1:発音： https://www.youtube.com/watch?v=gObvG7zn1pM

*2:発音： https://www.youtube.com/watch?v=-RbbG5Xh8Qs

*3:二重圏を使うアイディアはネステルの発案です。ネステルのもともとの動機は並列計算の記述だったようです。

*4:パレが「縦・横」をまったく使わないわけではないです。