テレオロジー圏、コンパクト閉圏、トレース付きモノイド圏などのあいだの親族的関連性を調べたい、という動機から資料を探しているうちに、二重圏を使う手法に出会いました。そのことを前の記事に書きました。
モノイド圏を調べるために、単一対象二重圏に埋め込んでみる、というのは良い方法だと感じました。各種モノイド圏のあいだの親族的関連性も見えやすくなります。
モノイド圏を埋め込む先の二重圏は、コーナーと呼ばれる特別な2-射の族を持っています。コーナー(の族)を備えた単一対象二重圏をコーナリング圏〈cornering category〉と呼ぶことにします。ネストル〈Chad Nester〉達はコーナリング圏を単にコーナリング〈cornering〉と呼んでいます。
「グリッド計算とコーナリング、そして二重圏」において、コーナリング圏が備えるコーナーの種類を次の図で示しました。
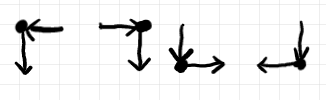
コーナーの縦方向のワイヤーは全部下向きなんですよね。
ネストルの動機は並列処理の定式化で、縦方向は時間方向とみなします。時間を逆方向に進むことはできないので、「縦方向のワイヤーは下向き」は当然の仮定になります。
しかし、縦方向を時間と解釈しないケースもあります。縦方向に逆行できるなら、コーナーの種類は次の8種になります。
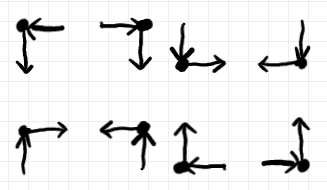
上に向かうワイヤーを認めているので、もとにする圏でも対象・射の逆転〈反転〉が必要です。つまり、もとにするモノイド圏として双対付き圏〈category with duals〉を要求します。
コーナーの種類が8種あると、次のようなワイヤー・ベンディング(180度の曲がり)を作れます。
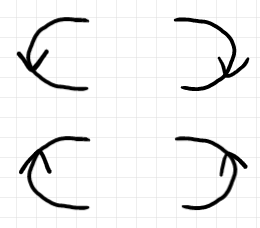
縦方向下向きのコーナーだけだと、上段のベンディングしか作れません。それだと、双対性(ニョロニョロ関係式)の半分しか記述できません。
もとにするモノイド圏が持っている構造や性質、埋め込み先(として構成する)コーナリング圏の構造や性質により、諸々の状況が変化します。この変化を観察することにより、各種モノイド圏のあいだの親族的関連性も見えてくるでしょう。