モノイド圏上のテンプレート・オペラッド：具体例とソフトウェア的解釈

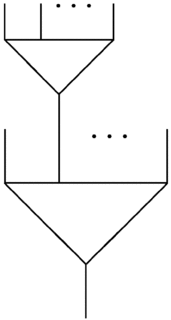
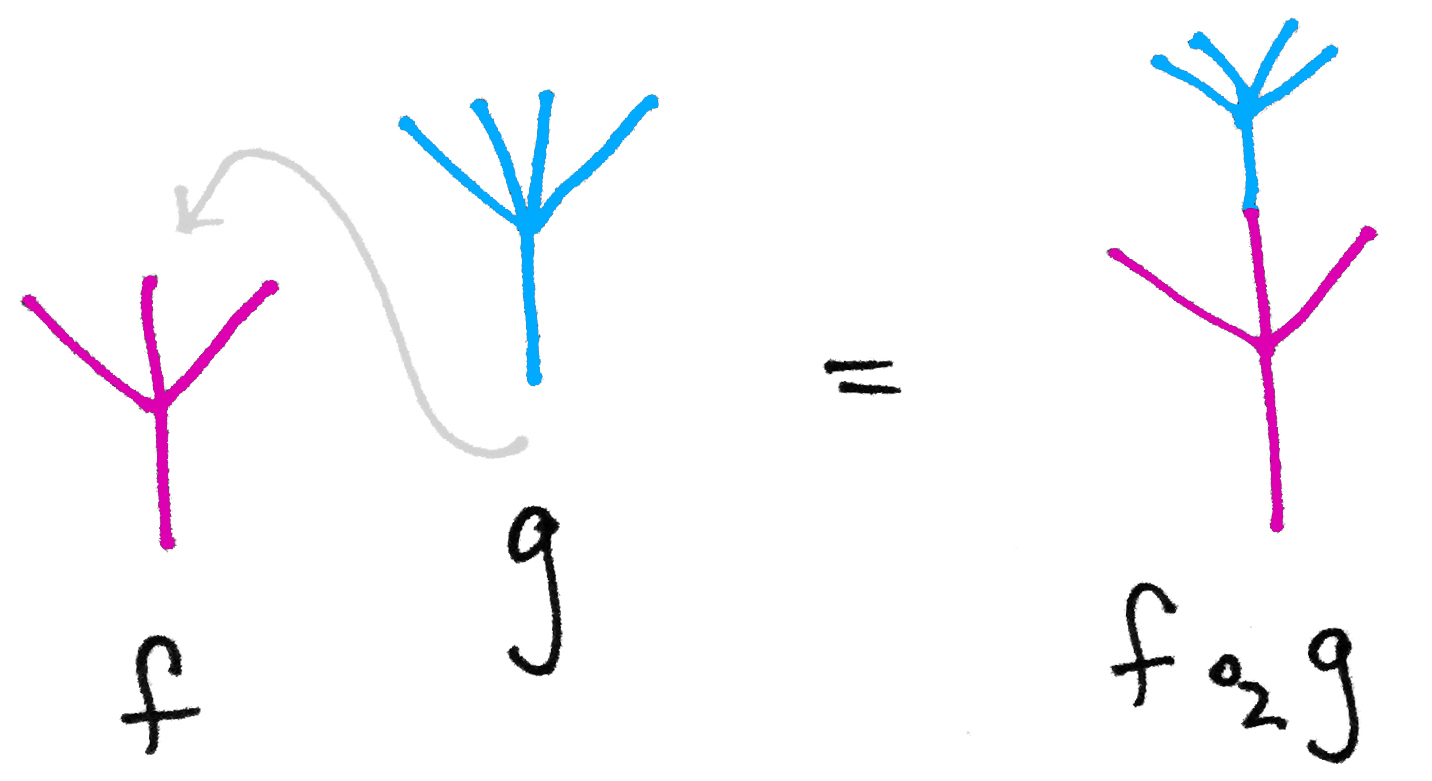とあるソフトウェア的な動機から、圏論的な代数系を構成してみます。この代数系は、通常の圏〈ordinary category〉とは違い、横結合、縦結合、モノイド積の3つの演算を持ちます。通常の圏は結合だけしか持たないし、モノイド圏は結合とモノイド積しか持ちません。では、モノイド2-圏〈monoidal 2-category〉*1かというと、そうではありません。モノイド二重圏〈monoidal double category〉*2かというと、そうでもありません。

横結合は、複圏〈オペラッド〉の結合であり、縦結合とモノイド積は、複圏の結合と整合する形に定義されます。こういう構造を何と呼ぶのかな？ とりあえず「圏上の複圏〈オペラッド〉」と呼んでおきます（つまんねー呼び名）。複圏とオペラッドは同じものです。複圏とオペラッドを区別する人もいます*3が、僕は同義語として使います。以下、複圏＝オペラッド として読んでください。

老婆心で注意すると； 縦結合／横結合の「縦・横」に何の根拠もありません。2つの結合演算があるので、それらをテキトー（ほんとにテキトー）に「縦」と「横」と呼び分けただけです。こういう、何の必然性もない選択については「根拠なき選択」を参照。

内容：

オペラッド

複圏〈multicategory〉をメチャクチャに手短に説明すると； 圏が“射の集まり”であるのに対して、複圏は“複射〈multimorphism | multiarrow〉（オペレータ〈operator〉またはオペレーション〈operation〉とも呼ぶ）の集まり”です。圏の射が1入力・1出力の関数を（極端に）抽象化したものであるのに対して、複圏の複射はn入力・1出力の関数を抽象化したものです*4。複圏をオペラッド〈operad〉とも呼びます。

[補足] [追記]
この記事では「オペレータ」を使ってますが、「オペレーション」が多いようです。修正はしませんが、「オペレーション」が一般的な用語だと注記しておきます。
[/追記] [/補足]

オペラッドの事例として、小円板オペラッド〈little disks operad〉が有名です。小円板オペラッドのオペレータは、大きな円板から小さな円板をくり抜いて穴を開けたモノです。下の写真は実物（金属製フランジ）ですが、もちろんオペレータは幾何的・代数的な対象物として抽象的に定義されます。

*5

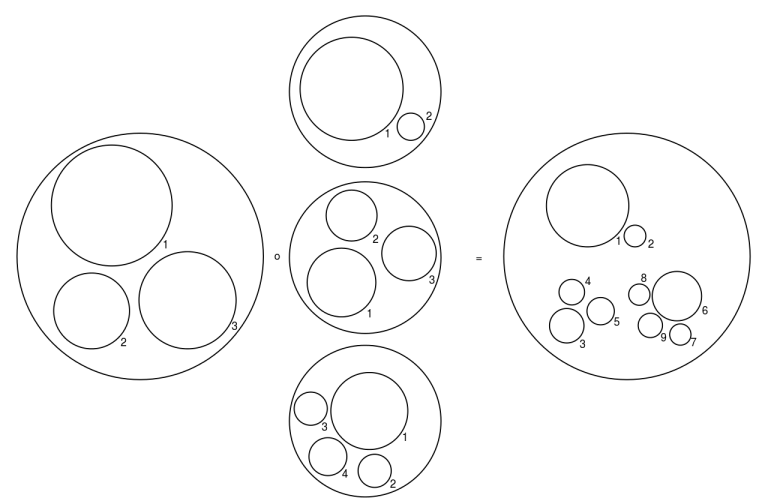
“穴＝小円板”の個数 k により、k-穴オペレータ〈operator with k-holes〉*6と呼ぶことにします。ひとつのk-穴オペレータと、k個のオペレータ達（それらの穴の個数は何でもよい）を“結合”することができます。次の図は Wikipedia項目 Operad -- "Little something" operads からのコピーで、オペラッド結合〈operadic composition〉を説明するものです。

*7

一番左のオペレータ（円板）が3-穴オペレータで、それに対して中程の3つのオペレータをオペラッド結合して、右のオペレータが作られます。左の3-穴オペレータのそれぞれの穴に、中程のオペレータを（サイズは適当に調整して）はめ込むのです。

左のオペレータを T、中程の3つのオペレータを S₁, S₂, S₃ とすると、これらのオペラッド結合は T(S₁, S₂, S₃) と書きます。描画方向／書字方向を逆にした場合は (S₁, S₂, S₃);T です。

のっぺらぼうな円板ではなくて、模様が描かれている円板を考えましょう。

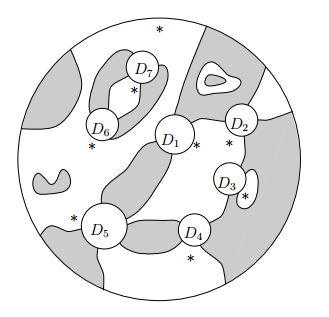
ここで、D₁, D₂, D₃, D₄, D₅, D₆, D₇ は穴なので、これは7-穴オペレータです。

次はオペラッド結合の例で、3-穴オペレータ T の2番目の穴 D₂ を2-穴オペレータ S で埋めています。

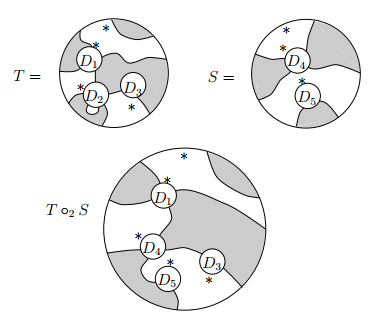
このように、全ての穴とはいわず、どれかひとつの穴を埋める形の結合は TS のように書きます。この例では i = 2 なので TS です。

模様付き穴あき円板の絵は、ジョーンズの次の論文からの引用〈コピー〉です。

• Title: Planar algebras, I (1999)
• Author: Vaughan F. R. Jones
• Pages: 122p
• URL: https://arxiv.org/abs/math/9909027

頭に変な物*8をかぶったこの人(↓)がジョーンズです。

*9

ジョーンズは、上の絵のような小円板オペレータを平面タングル〈planar tangle〉と呼んでいます。穴が1個だけの平面タングルだけを考え、模様の二色塗り分け〈網掛け〉をやめて線だけの模様にしたものを単純平面タングル〈SPT | simple planar tangle〉と呼ぶことにします*10。単純平面タングルの全体は、通常の圏になります。単純平面タングルの圏は、昔（2009年）、セミナーの題材に使ったことがあります。

• モニャドセミナー2の資料やら補足やらナニヤラ

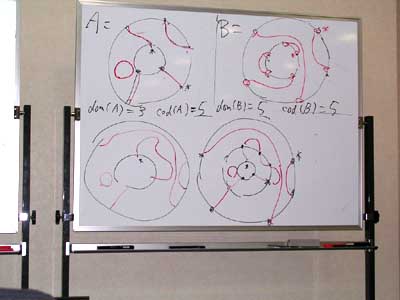
このセミナーの後で、参加者の田辺さんが、単純平面タングルのデモを作ってくれました。

• 田辺さんの圏論デモ、こりゃオモロー
• 田辺さんの単純平面タングル（SPT）圏デモの画面ショット

このデモの画面ショットを再掲します。

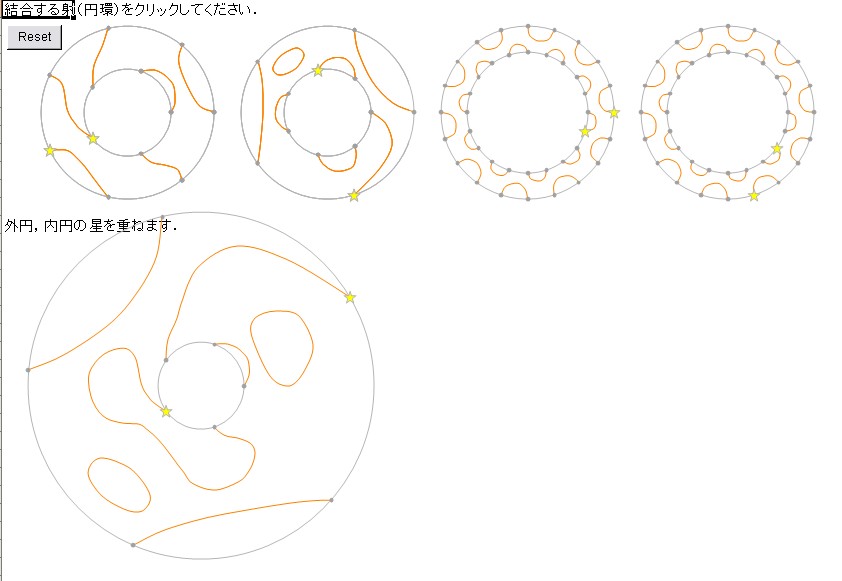
画面(↑)の上の段の4つは、単純平面タングルの事例です。左から順に1番から4番、T₁, T₂, T₃, T₄ とします。T₃ = T₄ です。よーく見ると、3番と4番で黄色い星（基準点）の位置がズレてますが、こいう違いは無視してイコールとみなします。1番の単純平面タングルと2番の単純平面タングルを結合すると、下の段の（大きめに描かれた）単純平面タングル T₂T₁ になります。2番の円板の穴に、1番の円板をはめ込んだものです。

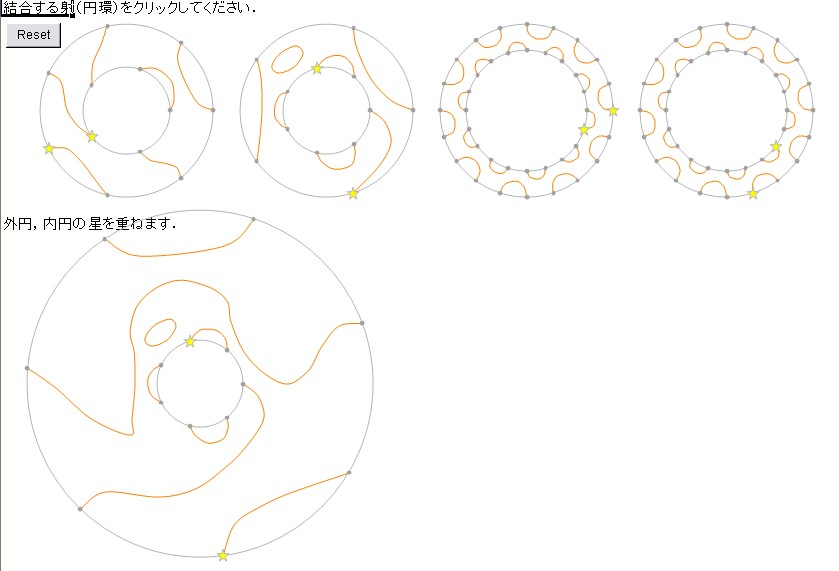
そして次は、2番と1番の（この順での）結合 T₁T₂ （反図式順結合記号なので、右から左に読むことに注意）です。1番の円板の穴に、2番の円板をはめ込みます。

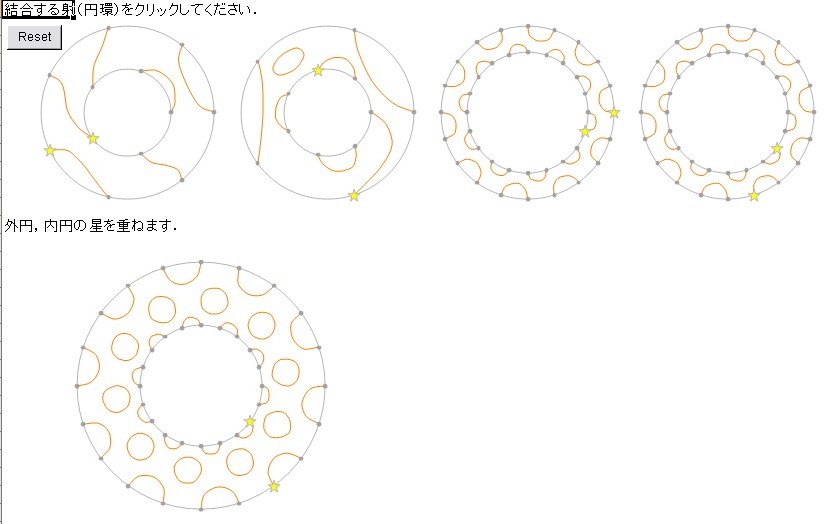
3番と4番の結合 T₄T₃ は次のよう。T₄ = T₃ だったので、これは自己結合 T₃T₃ です。

単純平面タングルの圏〈Annular Temperley-Lieb Category〉について、より詳しくは：

• Title: A Cyclic Approach to the Annular Temperley-Lieb Category (2009)
• Author: David Penneys
• Pages: 35p
• URL: https://arxiv.org/abs/0912.1320

テンプレート展開処理（回想含む）

前節の単純平面タングルは、圏の（もともとは複圏の）面白い例としてセミナーで使いました。では「単なる面白い例」だったのでしょうか？ そうではなくて、当時の僕の個人的な興味から調べていたネタでもあるのです。

記事「モニャドセミナー2の資料やら補足やらナニヤラ」の日付を見てみましょう。2009年5月22日です。その前後で、僕は次のような記事を書いています。

• 2009年4月8日 「PFTL: 純関数型テンプレート言語、発端とToy言語」 （サンプルコードがErlangだ、懐かしい）
• 2009年6月4日 「テレンス・パーのMVCR (Model-View-Controller-Renderer) 方式はどうなんだろうか」
• 2009年6月5日 「厳密分離の原理とテンプレートエンジン」

これらの記事はテンプレート言語とテンプレートエンジンに関するもので、当時の僕の発想は：

まー要するに、テンプレート言語を、機能制限された純関数型言語と考え、テンプレートエンジンはその実行系と考えりゃいい、ってことです。

テンプレート言語の構文を新しく作る気はありませんでしたが（実際、PHP Smarty の構文を拝借した）、テンプレート処理の方式と原理はハッキリさせたかったので、オペラッド〈複圏〉の計算を想定していました*11。

「テンプレート言語は機能制限された純関数型言語」なので、テンプレートは関数の表現と考えられます。複数のテンプレート変数〈プレースホルダー〉を持つので、多変数関数です。多変数関数の抽象化としてオペラッドのオペレータ〈複圏の複射〉が適切だろう、というわけです。

k-穴オペレータ T を、番号で識別されたk個のテンプレート変数を持つテンプレートと考えます。k個のオペレータのリスト (S₁, ..., S_k) は、テンプレートの展開コンテキスト（テンプレートに渡すk個の引数リスト）に相当し、オペラッド結合（の結果） T(S₁, ..., S_k) は、テンプレート展開処理（の結果）とみなせます。

20世紀の頃から、僕の主たる仕事が文書処理だったこともあり、テンプレート展開処理は随分昔から考えてはいました。2009年前後はオペラッド・ベースのテンプレート展開処理を主に（背景原理として）利用してましたが、モナド・ベースで考えることもできます（以下は2007年初頭の記事）。

• 圏論やモナドが、どうして文書処理やXMLと関係するのですか？

2005年より前、トレース付きモノイド圏〈traced monoidal category〉やコンパクト閉圏〈compact closed category〉をベースに考えていた内容の一部は、キマイラ・サイトに残骸が残ってます*12が、僕も、その頃のことはあんまり憶えてません。ただ、このブログ内（2005年以降）でも、トレース付きモノイド圏やコンパクト閉圏の話はけっこうしています。

ソフトウェアによる何らかの処理があるとき、その抽象モデルとして、トレース付きモノイド圏／コンパクト閉圏／モナド／オペラッド〈複圏〉／その他 のどれが適切なのか？ それらの相互関係はどうなっているのか？ といった基本的〈fundamental〉な問題は、いまだによく分かりません。どうやら、分からないまま死んでしまいそうです。

円板以外の絵の描き方

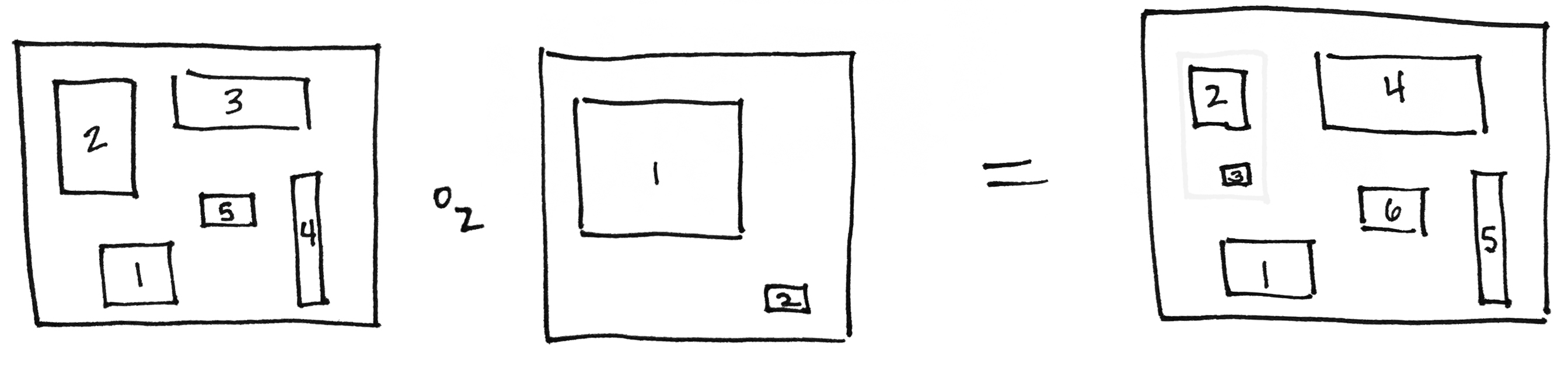
大きな円板から、k個の小さな円板〈little disks〉をくり抜いたモノがk-穴の小円板オペレータでした。円板ではなくて、方体〈cube〉でもかまいません -- 小方体オペレータ〈little cubes operator〉です。下の図は、円板の代わりに四角形〈2次元方体〉を使って描いたオペラッド結合の絵です。左側の四角板の2番の穴に、まんなかの四角板を（縮小して）はめ込むと、右側の6個の穴を持つ四角板になります。穴の番号付け〈ナンバリング〉は適宜調整〈リナンバリング〉します。

*13

穴あきの円板や四角形を描く代わりに、ツリーによってオペレータとオペラッド結合を表すこともできます。次の図では、オペレータはツリーで、穴はツリーの末端〈葉 | リーフ〉で表しています。オペラッド結合は、接ぎ木〈grafting〉操作となります。

*14

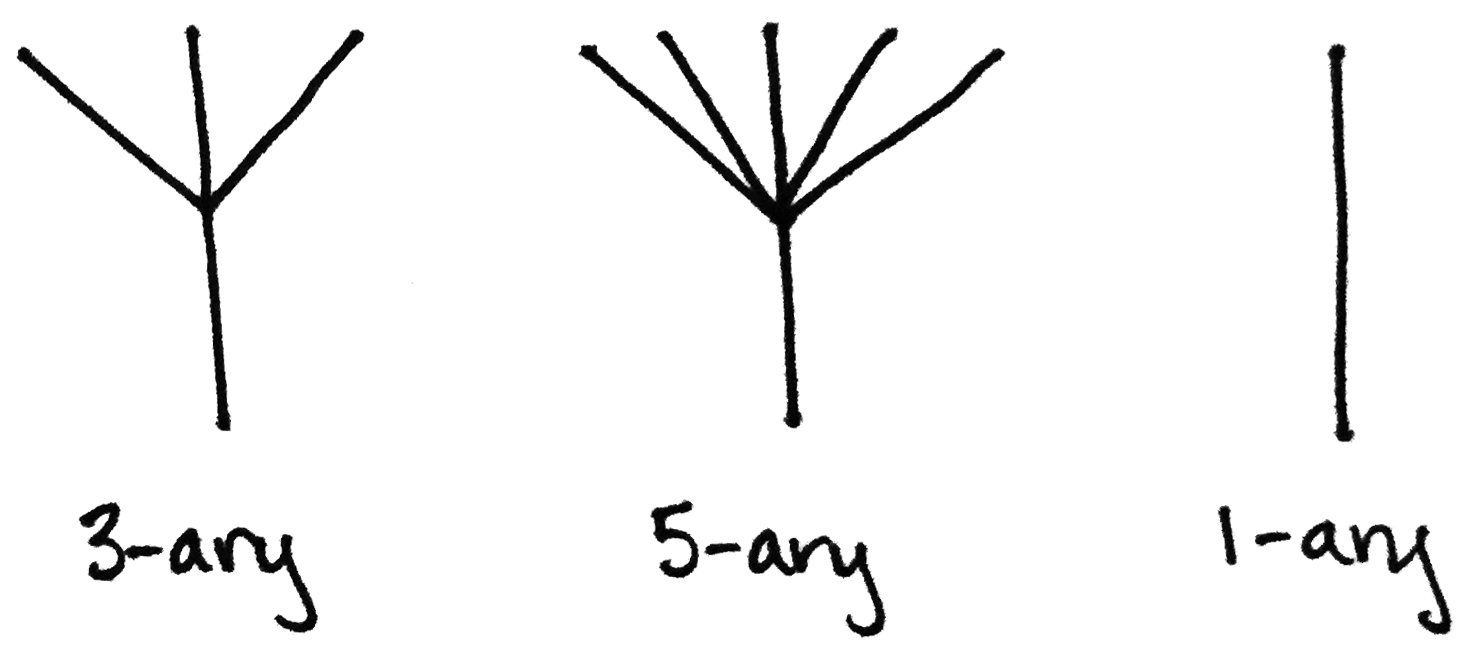
ツリーになると、k-穴オペレータという言い方はおかしいので、穴の数を項数〈arity〉と呼び、k-項オペレータ〈k-ary operator〉と、普通の言い方をします。

*15

この節で引用（拝借）した図は、次のブログ記事にあったものです。

1. What is an Operad? Part 1
2. What is an Operad? Part 2

英語ですが、オペラッド入門として分かりやすい記事で、おすすめです。

MathOverflow に、次のような絵がありました。描画ソフトウェアでオペレータやオペラッド結合を描くときは、こんな描き方が向いているでしょう。

*16

ストリング図とプログラム処理の記述

ストリング図に関しては、このブログ内で死ぬほどイッパイ書いているので、ひとつだけ記事を挙げると：

• 圏論の随伴をちゃんと抑えよう： お絵描き完全解説

この記事の前半（以下に目次）がストリング図の描画法の話です。ここを読めば、圏の圏のストリング図を描けるようになると思います。モノイド圏の場合は、対象←→線〈ワイヤー〉、射←→点〈ノード〉 と対応させ、面〈エリア | 領域〉は単なる背景だとします。

1. 圏の圏における絵算
   1. 圏と関手 F:C→D
   2. 自然変換 α::F⇒G:C→D
   3. 関手の結合
   4. 自然変換の縦結合
   5. 自然変換の横結合
   6. 事例
   7. 恒等関手
   8. 恒等自然変換
2. 対象と射の格上げ
3. 図式順記法と混合記法

プログラムによる処理をストリング図で記述するには、処理単位をノードで描き、データと制御の流れをワイヤーで描きます。この約束で描かれたストリング図は、古来よりフローチャートと呼ばれ、プログラマには忌み嫌われてきました*17。しかし僕は、常にフローチャートの味方です。

• フローチャートをめぐる迷信と妄言と愚昧 (2012年)
• 「フローチャート」騒ぎ、もう少し頭使って考えてみようよ (2016年)

ストリング図を愛用している僕が、ストリング図の特定利用形態であるフローチャートを嫌うわけがありません！

さて、今までの節で、穴あき円板や穴あき四角板と、穴へのはめ込み操作（オペラッド結合）が登場しました。ジョーンズの平面タングルでは、円板に模様が描かれていました。我々は、穴あき四角板の（穴じゃない部分に）ストリング図を描くことにします。ストリング図が描かれた穴あき四角板は、穴をテンプレート変数〈プレースホルダー〉とみなしてテンプレートなので、ストリング図テンプレート〈string diagram template〉と呼ぶことにします。

まず、四角い板（四辺形の境界で囲まれた領域）に普通のストリングを描いています。例えば：

こういう穴なしの板もストリング図テンプレートの特殊なモノです。たまたま、穴の個数〈項数〉が0のテンプレートです。

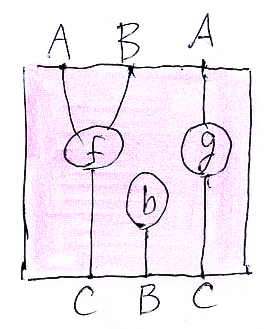
次に、fがあった場所に四角い穴をあけます。次のような1-穴〈単項の〉のストリング図テンプレートができます。

このストリング図テンプレートを T と名付けましょう。T に描かれた“模様＝ストリング図”がどうであるかは脇において、テンプレートとしての仕様（プロファイル〈profile〉と呼ぶ）について考えます。以下では、「穴その1」と書く代わりに $1 と書きます。テンプレート変数っぽいでしょ、1番のプレースホルダーってことです。

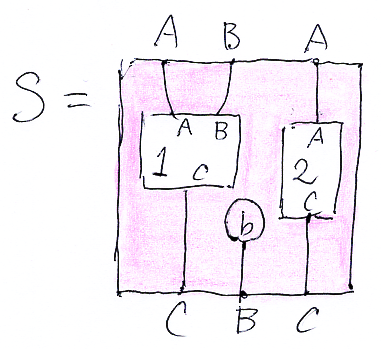
プレースホルダー $1 のプロファイルは $1:A,B→C と書けます。見ての通り、AとBのワイヤーが入り、Cのワイヤーが出るはずの穴だからです。外側の四角板のプロファイルは A,B,A→C,B,C なので、Tのプロファイルは T::($1:A,B→C)⇒(A,B,A→C,B,C) と書くことにします。これは穴〈プレースホルダー | テンプレート変数〉が1つの場合で、以下のように2つの穴があれば、テンプレートのプロファイルは S::($1:A,B→C),($2:A→C)⇒(A,B,A→C,B,C) です（二項テンプレート）。

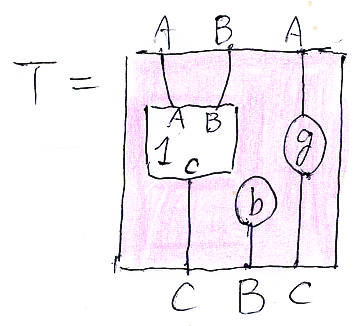
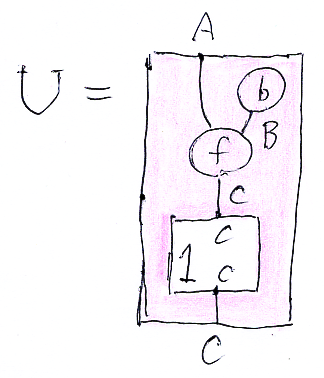
ストリング図テンプレート U は次の図のごときとします。Uのプロファイルは U::($1:C→C)⇒(A→C) です。

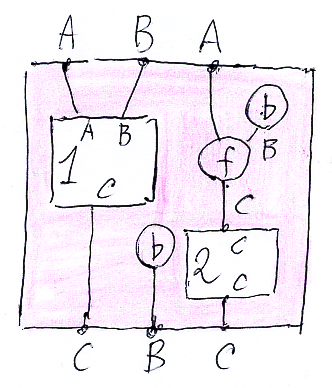
オペラッド結合 SU を作ると、次のようになります。結合結果のプロファイルは SU::($1:C→C)⇒(A,B,A→C,B,C) です。穴〈プレースホルダー | テンプレート変数〉の番号はリナンバリングしてます。

プロファイルの記述において、($1:A,B→C),($2:A→C)⇒(A,B,A→C,B,C) は、(A,B→C),(A→C)⇒(A,B,A→C,B,C) のように $1, $2 を省略して書いても問題ありません。が、穴〈プレースホルダー | テンプレート変数〉の識別に番号ではなく名前を使うときは、名前の省略はできません。例えば、($x:A,B→C),($y:A→C)⇒(A,B,A→C,B,C) のように。

モノイド圏上のテンプレート・オペラッド

ここからの話は、形式的かつ急ぎ足（雑とも言う）になります。前節まで、事例を出し直感的な話をしてきたので、それほど難しくはないと思います。

Cはモノイド圏 (C, , I, α, λ, ρ) だとします。いつものように記号の乱用〈abuse of notation〉をしています。α, λ, ρ は律子ですが、知らなかったら気にしなくてもいいです。

C内での通常の計算、つまり圏の結合とモノイド積を使った計算以外に、テンプレート処理をしたいとします。このとき、テンプレートとしてストリング図テンプレートを使います。Cの対象と射でラベルされたストリング図テンプレートの全体を SDT(C) としましょう。

集合*18 SDT(C) の要素、つまりストリング図テンプレートは、前節で説明したプロファイルを持ちます。そのプロファイルは二段階構成になっていて、穴または四角板のプロファイルを組み合わせてストリング図テンプレートのプロファイルを構成しています。ややこしい。穴の周囲と外側の四角板の周囲は、2次元図形の境界を形成します。なので、穴または四角板のプロファイルは仮に境界プロファイル〈boundary profile〉と呼ぶことにします。そして、ストリング図テンプレートのプロファイルはテンプレート・プロファイル〈template profile〉です。

個々の境界要素（穴の周囲と四角板の周囲）の境界プロファイルは、|C|^*×|C| の要素とみなしてかまいません。ここで、|C|^* の右肩の星はクリーネスターで、Cの対象のリストの集合です。(A₁, ..., A_n)∈|C|^* と B∈|C| のペア ((A₁, ..., A_n), B) が境界プロファイルですが、それを (A₁, ..., A_n)→B とか A₁, ..., A_n→B と書くのです。

α₁, ..., α_k, β が(k + 1)個の境界プロファイルのとき、テンプレート・プロファイルは (α₁, ..., α_k)⇒β の形です。つまり、テンプレート・プロファイルの集合は (|C|^*×|C|)^*×(|C|^*×|C|) です。二重矢印'⇒'を使ったのは、境界プロファイルと混同しないようにです。

[補足] [追記]
テンプレート・プロファイルの集合が (|C|^*×|C|)^*×(|C|^*×|C|) である、という事実が重要です。集合 (|C|^*×|C|)^*×(|C|^*×|C|) の要素をどのように書き表すかは恣意的な決定となります。区切り記号として、カンマ以外に'→'や'⇒'を選んだことも、根拠なき選択です。別なタイミングでは、また別な根拠なき選択をするでしょう。
[/追記] [/補足]

(α₁, ..., α_k)⇒β がテンプレート・プロファイルのとき、このプロファイルを持つテンプレートの全体を SDT(C)(α₁, ..., α_k⇒β) と書くことにします。T∈SDT(C)(α₁, ..., α_k⇒β) ならば、ストリング図テンプレート T はk個の穴〈プレースホルダー | テンプレート変数〉を持ち、それぞれの穴の境界プロファイルは α₁, ..., α_k であり、外側の四角板のプロファイルは β です。次が成立します。

• T∈SDT(C)(α₁, ..., α_k⇒β) ⇔ T::α₁, ..., α_k⇒β

SDT(C) は、すべてのテンプレート・プロファイル α₁, ..., α_k⇒β に対するオペレータ集合 SDT(C)(α₁, ..., α_k⇒β) 達を寄せ集めたものです。既に説明したテンプレート展開処理が、オペラッド結合を与え、その他、オペラッド〈複圏〉として必要なモノや性質を持つので、SDT(C) はオペラッド〈複圏〉になります。オペラッド結合を横結合〈horizontal composition〉とも呼びます。

オペラッド SDT(C) は、"横結合＝オペラッド結合＝テンプレート展開”だけではなく、縦結合とモノイド積を持ちます。縦結合〈vertical composition〉は記号';'（これは図式順結合記号）、モノイド積〈monoidal product〉は記号''として、いずれもCの結合／モノイド積とオーバーロードします。

ストリング図テンプレートの縦結合は、まったく自由にできるわけではなくて、縦結合すべきストリング図テンプレートのプロファイルに制約があります。

  S∈SDT(C)(α1, ..., αk⇒A1, ..., Ap→B1, ..., Bq)
  T∈SDT(C)(β1, ..., βℓ⇒B1, ..., Bq→C1, ..., Cr)
  --------------------------------------------------- ↓縦結合
  S;T∈SDT(C)(α1, ..., αk,β1, ..., βℓ⇒A1, ..., Ap→C1, ..., Cr)

縦結合は、ストリング図テンプレートの四角板を（今までの描画方向で）縦に並べてワイヤーを繋ぐ操作です。縦結合が縦並びなるのは作為的に揃うような描画法を選んでいるからで、なんらの必然性もありません。

モノイド積は、特に制約はなくて自由にできます。

  S∈SDT(C)(α1, ..., αk⇒A1, ..., Ap→B1, ..., Bq)
  T∈SDT(C)(β1, ..., βℓ⇒C1, ..., Cq→D1, ..., Dr)
  --------------------------------------------------- ↓モノイド積
  S⊗T∈SDT(C)(α1, ..., αk,β1, ..., βℓ⇒A1, ..., Ap, C1, ..., Cr→B1, ..., Bq, D1, ..., Dr)

モノイド積は、ストリング図テンプレートの四角板を横に並べる操作です。

縦結合とモノイド積の描画は、テンパリー／リーブ圏における絵の描き方が参考になるかも知れません。注意すべきは、下の絵の'∘'はオペラッド結合ではなくて我々の縦結合';'の反図式順記号であることです。あと、下図の結合の描画方向は ↑ です。そもそも、図式順記法と反図式順記法を混ぜるとストレスを招くので、どちらかに揃えたほうがいいですけどね。

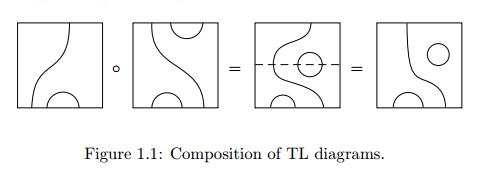
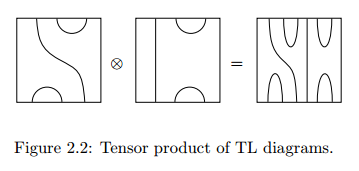
上の絵は、次の論文からの引用〈コピー〉です。

• Title: The Temperley-Lieb categories and skein modules (2014)
• Author: Joshua Chen
• Pages: 74p
• URL: https://arxiv.org/abs/1502.06845

ストリング図テンプレートとテンパリー／リーブ圏が密接に関連しているわけでもないですが、興味があれば：

• テンパリー／リーブ圏とカウフマンのスケイン関係式
• 単純平面タングルとカウフマン図のキャンバス・基準点について

最後に、テンプレート処理の表示的意味論〈denotational semantics〉にちょっと触れておきます； 穴〈プレースホルダー | テンプレート変数〉を1個も持たないストリング図テンプレートの集合 SDT(()⇒A₁, ..., A_p→B₁, ..., B_q) は、通常のストリング図の集合と同じことです。集合 SDT(()⇒A₁, ..., A_p→B₁, ..., B_q) から、モノイド圏Cのホムセット C(A₁ ...A_p, B₁ ...B_q) への標準的な意味写像が存在します。この標準的意味写像をもとに、ストリング図テンプレートの表示的意味論を構成することができます。最初に与えたモノイド圏Cは、関数計算（結合とモノイド積）とテンプレート計算（展開処理*19）の意味論を支える圏なのです。

*1:例えば、圏の圏（厳密2-圏になる）に直積を一緒に考えると、モノイド2-圏になります。

*2:例えば、モノイド圏の可換四角形の二重圏はモノイド二重圏になります。「二重圏のもっと簡単な例：圏の可換四角形の二重圏 」参照。

*3:単一対象の複圏がオペラッドであり、色付きオペラッド〈colored operad〉が複圏だと言う人がいます。対称群による作用をオペラッドの定義に含める人もいます。そこらへんは色々。

*4:n入力・m出力の関数を抽象化したものは多射〈polyarrow〉で、多射の集まりが多圏〈polycategory〉です。

*5:画像は https://www.carchemistry.com/baffle-builder-round-flange-disk/

*6:「穴」は、「アナ」でも「ケツ」でも、どっちでもいいです。どっちも下品な響きですが。

*7:画像は https://en.wikipedia.org/wiki/Operad#/media/File:Composition_in_the_little_discs_operad.svg By Ladislav_the_Posthumous (talk) (Uploads) - Own work, GFDL, https://en.wikipedia.org/w/index.php?curid=13907966

*8:被り物としては変ですが、木製の民芸品のようです。7成分のボロミアン環類似な図形なんだとか。

*9:画像は https://www.math.toronto.edu/drorbn/Gallery/KnottedObjects/GhanaianBorromean

*10:単純平面タングルの形状は円環なので、円環タングル〈annular tangle〉、あるいは単に円環〈annulus〉とも呼ばれます。

*11:実用上・実際上の制約から、オペラッド計算をそのまま実装したわけじゃないです。

*12:1990年代から2005年のあいだに、僕が考えたり実際にやったことをHTML文書にして公開するためにキマイラ・サイトを始めましたが、すぐにブログ（当時の「はてなダイアリー」）に移行したので、キマイラ・サイトは長年放置状態です。

*13:画像は https://uploads-ssl.webflow.com/5b1d427ae0c922e912eda447/5b58d5b0f848c8fd7ff73ecb_comp.jpg

*14:画像は https://uploads-ssl.webflow.com/5b1d427ae0c922e912eda447/5b58d15cd283c6d6bc7522b4_2.jpg

*15:画像は https://uploads-ssl.webflow.com/5b1d427ae0c922e912eda447/5b58cf8680211ab1b1f5055f_1.jpg

*16:画像は https://i.stack.imgur.com/LdJMH.gif

*17:どんな図をフローチャートと呼ぶか？ という定義の問題はあります。僕は、ハッキリした定義をせずに「フローチャート」と言っています。嫌っている人々もハッキリした定義をせずに嫌っているので、それでもいいだろう、と。もしハッキリした定義を提示する人がいるのなら、それに基づいた議論をすることにやぶさかではありません。

*18:大きな集合かも知れません。

*19:同義語がたくさんあります。{テンプレート | マクロ | シェマ | パターン}の{展開 | 置換 | 代入}処理