応用圏論〈Applied Category Theory〉においても、コエンド〈coend〉の利用は増えています。例えば、“オプティックの圏”のホムセットの構成にはコエンドを使います。
ところが、コエンドの説明が(僕自身の説明も含めて)だいたいは不親切で、「細かい事まで言わずとも、察して悟れ」というスタイルで書かれていることが多いですね。
例えば、コエンドの“定義”として、次のような図式でお茶を濁すことがしばしばあります。
$`\quad \displaystyle{\coprod_{X \to Y} P(Y, X)
\begin{matrix}{\to}\\{\to} \end{matrix}
\coprod_{X} P(X, X) \to \int^{X} P(X, X)
}`$
これは雑すぎて、いくら一生懸命に眺めても(普通の人では)何も分かりません*1。考えても無駄で、「感じるんだ、悟るんだ。〈Don't think. Feel.〉」の世界になっています*2。

コエンドの定義、特にコエンド同値関係について、(なるべく)悟らないでも分かるように説明します。$`\newcommand{\cat}[1]{ \mathcal{#1}}
\newcommand{\mrm}[1]{ \mathrm{#1}}
\newcommand{\In}{ \text{ in }}
\newcommand{\Iff}{\Leftrightarrow}
\newcommand{\op}{\mathrm{op}}
\newcommand{\id}{\mathrm{id}}
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
%`$
内容:
関手ボックスによる説明
このブログの過去記事「米田テンソル計算 1: 経緯と発想 // 関手ボックス」において、コエンド同値関係の説明をしています。
コエンドの具体的構成で使われるコエンド同値関係も、関手ボックスを使って次のように描けます。
絵に続けて、箇条書きで説明も書いています。僕は、これでコエンド同値関係の“完全な説明”になっていると思ってしまう(錯覚)のですが、実際のところ「細かい事まで言わずとも、察して悟れ」スタイルに陥っています。何がダメかと言うと:
- 関手ボックスに慣れてないと絵の解釈ができない。
- 絵が解釈できても、テキスト(記号的表現)との対応がとれない。
という次第なので、絵だけではなくテキスト(記号的表現)についても触れ、「絵←→テキスト」の相互翻訳も説明します。
コイコライザー
基本的な概念・構成の話から始めましょう。
コエンドを具体的に作るとき、集合圏におけるコイコライザー〈coequalizer | 余等化子〉の概念が必要になります。コイコライザーはイコライザー〈equalizer | 等化子〉の双対概念です。
イコライザーとコイコライザーは、次のような、射(集合圏では写像)の平行対からスタートして考えます。
$`\xymatrix {
A \ar@/^/[r]^{f} \ar@/_/[r]_{g}
& B
} \In {\bf Set}`$
与えられた平行対に対して、次の点線の射があれば、それはイコライザーの候補になります。
$`\xymatrix {
\cdot \ar@{.>}[r]^{?}
& A \ar@/^/[r]^{f} \ar@/_/[r]_{g}
& B
} \text{ where }?;f = ?;g \In {\bf Set}`$
イコライザー候補のなかでイコライザーを特徴づける性質は、圏論の普遍性(あるいは極限)を使って述べることができますが、ここでは具体的な作り方を示します。
次の部分集合を考えます。
$`\quad S := \{x\in A \mid f(x) = g(x)\}`$
この部分集合の埋め込み写像〈包含写像〉を $`e`$ とすると、$`e`$ が平行対 $`f, g`$ のイコライザーになります。
$`\xymatrix {
S \ar[r]^{e}
& A \ar@/^/[r]^{f} \ar@/_/[r]_{g}
& B
} \text{ where } e;f = e;g \In {\bf Set}`$
結局、イコライザーとは、方程式 $`f(x) = g(x)`$ の解集合 $`S`$ の埋め込み写像のことです。方程式の解集合は中学校以来お馴染みですよね。
双対的に考えて、与えられた平行対に対して、次の点線の射があれば、それはコイコライザーの候補になります。
$`\xymatrix {
A \ar@/^/[r]^{f} \ar@/_/[r]_{g}
& B\ar@{.>}[r]^{?}
& \cdot
} \text{ where } f;? = g;?\In {\bf Set}`$
コイコライザーも具体的に構成しましょう。集合 $`B`$ 上に、$`f, g`$ から定まる関係 $`\sim`$ を考えます。
$`\For y, y'\in B\\
\quad y \sim y' :\Iff \exists x\in A.( y = f(x) \land y' = g(x) )
`$
この関係 $`\sim \text{ on }B`$ は同値関係とは限りませんが、どんな関係〈二項関係〉に対しても、その関係を含む最小の同値関係が存在します。そのような同値関係を $`\simeq`$ とします。同値関係 $`\simeq`$ は次の性質を持ちます。
- $`x \simeq x`$
- $`x \sim y`$ ならば $`x \simeq x'`$
- $`x \simeq y`$ ならば $`y \simeq x`$
- $`x \simeq y`$ かつ $`y\simeq z`$ ならば $`x \simeq z`$
同値関係 $`\simeq`$ は平行対 $`f, g`$ から決まるので、$`\simeq_{f, g}`$ と書いておいたほうが正確です。
集合 $`B`$ 上の同値関係 $`\simeq_{f,g}`$ の商集合を作り、それを $`B/\simeq_{f,g}`$ とします。商集合への標準射影を $`p`$ としましょう。
$`\quad p: B \to B/\simeq_{f,g} \In {\bf Set}`$
こうして作った $`p`$ が、平行対 $`f, g`$ のコイコライザーを与えます。$`B/\simeq_{f,g}`$ を $`Q`$ という名前で呼ぶなら:
$`\xymatrix {
A \ar@/^/[r]^{f} \ar@/_/[r]_{g}
& B\ar[r]^{p}
& Q
} \text{ where } f;p = g;p \In {\bf Set}`$
イコライザーもコイコライザーも具体的に構成しましたが、イコライザー/コイコライザーは圏論的な概念なので、同型を除いて〈up-to-iso で〉一意的に決まります。ホントに一意的なわけではありません。今構成した $`S \overset{e}{\to} A`$ と $`B \overset{p}{\to} Q`$ は典型的なイコライザー/コイコライザーで、他にもイコライザー/コイコライザーは在ります。
イコライザー/コイコライザーの具体的な構成法が納得いったならば、極限/余極限としてイコライザー/コイコライザーの定義も確認しておくと良いでしょう。
多項関手のスイムレーン描画法
関手 $`F:\cat{C} \to \cat{D}`$ の図示法として、関手ボックス〈functor box〉、ストライプ図〈stripe diagram〉があります。$`F(f:A \to B)\In \cat{D}`$ を次のように描きます。
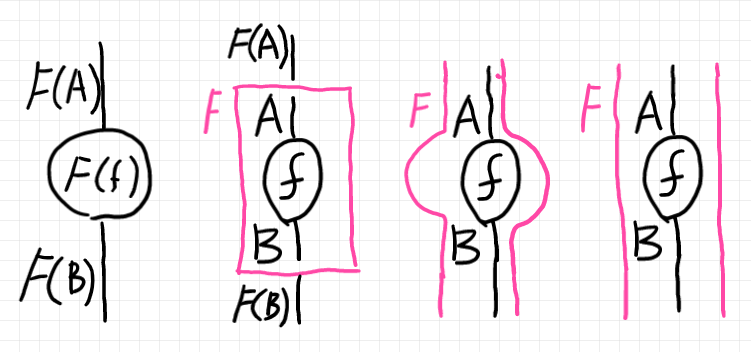
関手の値を、左端は単にワイヤー&ノードとして描いています。左から二番目は関手ボックスによる絵です。三番目は射の部分を膨らましたストライプ図、右端はストレートなストライプ図です。
$`\cat{C}`$ の対象・射を普通のストリング図として描いて、関手 $`F`$ を表すボックスまたはストライプ〈シース | sheath〉で包む、という描き方が関手ボックス/ストライプ図です。
圏論的な絵図を描くソフトウェアがあるとしたら、ワイヤーやノードをクリックするとボックスになったり、あるいはストライプに変形するようなUIが備わるでしょう。実体が変化するのではなくて、描き方/表示方法が変わるだけです。圏論的な絵図を描いたり操作できる対話的ソフトウェアがあるといいのですが、残念ながら存在しません。
なお、ストライプ図を使った計算の例は:
ストライプ図については何度も書いているので:
- 「ストライプ図」の検索結果
さてところで、後で出てくるプロ関手は、関手の一種であり、2つの圏の直積圏を域とします。そのような関手を双関手〈bifunctor〉と呼びますが、二項関手〈functor {with | of} two arguments〉と呼んだほうが分かりやすいし、三項関手、四項関手、‥‥、n項関手と一般化しやすいです。
多項関手〈n項関手 | functor {with | of} many arguments〉を図示するときは、ボックスやストライプの内部をスイムレーン〈swim lane〉に分けることにします。ボックス/ストライプの内部がn本のレーンに分かれていて、各レーンに関手の引数〈argument of functor〉を描きます。レーンの区切りは点線にしましょう。例えば、三項関手 $`G:\cat{C}\times\cat{D}\times\cat{E} \to \cat{A}`$ なら3つのレーンを持ったボックス/ストライプで描きます。
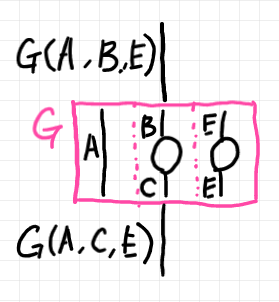
n-項関手の域に反対圏〈opposite category〉が含まれるときは、反対圏の射はレーンを逆行するように描きます。例えば、$`H:\cat{C}\times \cat{D}^\op \to \cat{A}`$ ならば、第二引数である $`\cat{D}`$ の射を逆行させます。
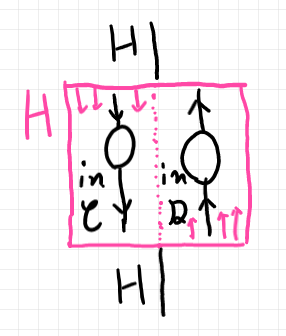
図のなかで下から上に逆行している射も、反対圏 $`\cat{D}^\op`$ の射としての方向は上から下です。
プロ関手と2レーン描画法
「プロ関手とは何であるか?」におおよそのイメージを抱くには、次の“比例式”が役に立ちます。
- 関数 : 関係 = 関手 : プロ関手
集合 $`A`$ から集合 $`B`$ への関係 $`R:A \not\to B`$ (この矢印で書くとする)は、関係圏〈category of relations〉の射ですが、実体としては部分集合 $`R\subseteq A\times B`$ です。部分集合は述語(ブール値集合 $`{\bf B}`$ への関数)で定義できるので、関係は関数 $`R:A\times B \to {\bf B}`$ とみなしてもかまいません。
似たような状況で、圏 $`\cat{C}`$ から圏 $`\cat{D}`$ へのプロ関手〈profunctor〉 $`P:\cat{C} \not\to \cat{D}`$ (この矢印で書くとする)は、プロ関手圏〈category of profunctors〉の射ですが、実体としては、プロ関手は関手 $`P:\cat{D}^\op \times \cat{C} \to {\bf Set}`$ です。圏を直積する順番が $`\cat{C}\times \cat{D}^\op`$ の逆なのが気になるかも知れませんが、単なる習慣です。他の習慣との整合性からこの順番を採用しているだけで特に意味はありません。
プロ関手(の実体)は集合圏への二項関手なので、2つのレーンを持つボックス/ストライプで描けます。2つの引数は反変-共変なので、第一引数が逆行〈backward〉、第二引数が順行〈forward〉です(あくまで習慣!)。人により場合により、共変-反変にするかも知れませんが、もちろん本質的な違いはありません。
2レーンの関手ボックス/ストライプは、順行方向が上から下、逆行方向が下から上で描くことにします。いつも注意してますが、描画方向の選択はまったく恣意的なので、人により場合により、あらゆる可能性があります。
プロ関手 $`P: \cat{D}^\op \times \cat{C} \to {\bf Set}`$ の2レーン関手ボックスは、例えば次のようになります。
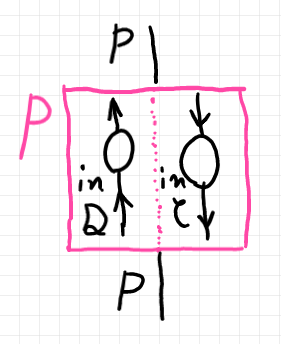
コエンドを定義するためのセットアップ
一般的なコエンドは、$`F:\cat{C}^\op \times \cat{C} \to X`$ という関手(圏 $`X`$ は良い性質を持つとして)に対して定義できます。が、ここでは $`X = {\bf Set}`$ の場合だけを考えます。つまり、ここでのコエンドは、自己プロ関手 $`P:\cat{C} \not\to \cat{C}`$ に対して定義されます。
今考えている圏 $`\cat{C}`$ は小さい圏だと仮定します。つまり、対象の集まり $`|\cat{C}|`$ や射の集まり $`\mrm{Mor}(\cat{C})`$ は通常の集合だとします。そうでないと、サイズの問題が出てきて厄介です。
自己プロ関手 $`P`$ のコエンドは、$`P`$ から作られた“写像の平行対”のコイコライザー(の余域)として定義されます。よって、コエンドを作る際のセットアップは次のようになります。
$`\xymatrix {
\boldsymbol{A} \ar@/^/[r]^{L} \ar@/_/[r]_{R}
& \boldsymbol{B}\ar@{.>}[r]^{?}
& \cdot
} \text{ where } L;? = R;?\In {\bf Set}`$
ここに出てくる $`\boldsymbol{A}, \boldsymbol{B}, L, R`$ を「察しろ」とか「悟れ」とか言わないでちゃんと定義します。これらがハッキリしたなら、コイコライザーの作り方は既に述べたので、コイコライザーの余域=コエンドが作れるはずです。
上記の図の $`\boldsymbol{A}`$ に相当する集合は次の集合です。
$`\quad \displaystyle{
\sum_{f\in \mrm{Mor}(\cat{C}) } P(\mrm{cod}(f), \mrm{dom}(f) )
}`$
$`\sum`$ は集合に対する総和記号です。$`\coprod`$ もよく使われますが、より馴染みがあるシグマにしました。圏 $`\cat{C}`$ のすべての射(すべての対象ではない!)$`f`$ に渡って、集合 $`P(\mrm{cod}(f), \mrm{dom}(f) )`$ 達を直和で足し合わせています。足し合わせるサマンド〈summand〉に $`P`$ が出現するので、$`P`$ から決まる集合です。
直和の定義をブレークダウンすると:
$`\quad \displaystyle{
\bigcup_{f\in \mrm{Mor}(\cat{C}) } \{f\}\times P(\mrm{cod}(f), \mrm{dom}(f) )
}`$
$`X = \mrm{dom}(f),\; Y = \mrm{cod}(f)`$ と置いて書き換えると:
$`\quad \displaystyle{
\bigcup_{ (f: X \to Y) \in \mrm{Mor}(\cat{C}) } \{f:X\to Y\}\times P(Y, X)
}`$
この集合の要素がどんなものかというと、射 $`f:X\to Y`$ と集合 $`P(Y, X)`$ の要素 $`s`$ のペア $`(f, s)`$ です。
さて次に、コイコライザーの図の $`\boldsymbol{B}`$ に相当する集合ですが、これは
$`\quad {\displaystyle
\sum_{X\in |\cat{C}|} P(X, X)
}`$
です。プロ関手 $`P`$ を対象 $`|\cat{C}^\op \times \cat{C}| = |\cat{C}|\times |\cat{C}|`$ 上に制限すると、集合係数の正方行列になりますが、その対角成分の総和、つまり正方行列のトレースに相当する量です。このトレース集合に、写像の平行対 $`L, R`$ から誘導される同値関係を入れて、その商集合を作ればコエンドを入手できます。
当然ながら、写像 $`L`$ と写像 $`R`$ をハッキリさせないと話になりません。それは次節で。
射の左作用と右作用
与えられたプロ関手 $`P:\cat{C} \not\to \cat{D}`$ に対して、写像 $`L`$ と写像 $`R`$ は次のようなプロファイル(域と余域)を持つのでした。
$`\quad \displaystyle{
\sum_{ (f: X \to Y) \in \mrm{Mor}(\cat{C}) } P(Y, X) \to
\sum_{ X \in |\cat{C}| } P(X, X) \In {\bf Set}
}`$
$`L`$ はleft、$`R`$ はrightのつもりで、左は第一引数、右は第二引数を意図しています。
上のプロファイルを少し書き換えます。
- 被っている束縛変数 $`X`$ を $`Z`$ に置き換える。「スコープが違う束縛変数は、被っても(同名でも)無関係」なのですが、意外と混乱・誤解する人が多いので、念のため。
- 直和を合併に書き換える。そのほうが具体性が増すと思うので。
$`L, R`$ のプロファイルは次のようになります。
$`\displaystyle{
\bigcup_{ (f: X \to Y) \in \mrm{Mor}(\cat{C}) } \{f:X\to Y\}\times P(Y, X) \to
\bigcup_{ Z \in |\cat{C}| } \{Z\}\times P(Z, Z) \In {\bf Set}
}`$
$`L, R`$ に引数を渡して戻り値を得るプロセスは次のようになります。
- $`\cat{C}`$ 内で、任意に適当な〈arbitrary〉対象 $`X, Y`$ と射 $`f:X \to Y`$ を選ぶ。
- 集合 $`P(Y, X)`$ の要素 $`s`$ を選ぶ。
- ペア $`(f, s)`$ を写像に渡す。
- 戻り値の情報として、$`\cat{C}`$ 内のとある対象 $`Z`$ が決まる。
- さらに、集合 $`P(Z, Z)`$ の要素 $`y`$ が決まる。
- ペア $`(Z, y)`$ が戻り値となる。
以上をまとめると、次のように書けるでしょう。
$`L, R:\;
(f:X\to Y, s\in P(Y, X)) \;\mapsto\; (Z, y\in P(Z, Z))
`$
簡略に書くなら:
$`L, R:\;
(f, s) \;\mapsto\; (Z, y)
`$
$`L, R`$ を具体的に定義するとは、与えられた $`(f, s)`$ から $`Z`$ と $`y`$ をどう計算するかの手順を具体的に書き下すことです。
$`L, R`$ を定義するために、その素材としてプロ関手 $`P`$ を使います。繰り返しになりますが、$`P`$ は次のような“集合間の写像”の族を定めます。
$`\For f:X→Y,\, g:S\to T \In \cat{C}\\
\quad P(f, g):P(Y, S) \to P(X, T) \In {\bf Set}
`$
特に、
$`\For f:X→Y,\, \id_X: X\to X \In \cat{C}\\
\quad P(f, \id_X):P(Y, X) \to P(X, X) \In {\bf Set}\\
\For \id_Y: Y\to Y,\, f:X→Y \In \cat{C}\\
\quad P(\id_Y, f):P(Y, X) \to P(Y, Y) \In {\bf Set}
`$
これを使って $`L, R`$ を具体的に書き下すと:
$`L(f, s) := (X, P(f, \id_X)(s)) \;\in \{X\} \times P(X, X)\subseteq \bigcup_{ Z \in |\cat{C}| } \{Z\}\times P(Z, Z)\\
R(f, s) := (Y, P(\id_Y, f)(s)) \;\in \{Y\}\times P(Y, Y)\subseteq \bigcup_{ Z \in |\cat{C}| } \{Z\}\times P(Z, Z)
`$
別な書き方をすれば:
$`\text{about }L\\
\For f:X\to Y,\, s\in P(Y, X)\\
\quad Z := X = \mrm{dom}(f)\\
\quad y := P(f, \id_X)(s)\\
\;\\
\text{about }R\\
\For f:X\to Y,\, s\in P(Y, X)\\
\quad Z := Y = \mrm{cod}(f)\\
\quad y := P(\id_Y, f)(s)
`$
$`f`$ を固定した場合の $`L, R`$ の軽量版を定義しておくと便利です。
$`L_f : P(Y, X) \to P(X, X)\\
\quad L_f(s) := P(f, \id_X)(s)\\
\:\\
R_f : P(Y, X) \to P(Y, Y)\\
\quad R_f(s) := P(\id_Y, f)(s)
`$
$`L_f`$ を、射 $`f`$ による左作用〈left action〉、$`R_f`$ を、射 $`f`$ による右作用〈right action〉といいます。$`P`$ (の一部)を集合係数の正方行列とみなすなら、左作用/右作用により、非対角成分も対角成分に変換されます。
固定した $`P`$ に対して、$`P(f, g)(s)`$ を、$`f, s, g`$ の三項に対する演算結果だと考えて $`f\cdot s \cdot g`$ と書くと、簡潔になって便利です。さらに、
$`\quad f\cdot s := f\cdot s \cdot \id,\, s\cdot g := \id \cdot s \cdot g`$
という略記も導入します。すると:
$`\quad L_f(s) := P(f, \id_X)(s) = f\cdot s \cdot \id = f\cdot s \\
\quad R_f(s) := P(\id_Y, f)(s) = \id \cdot s \cdot f = s\cdot f
`$
この書き方なら、左作用/右作用の“感じ”が出ます。
[/補足]
コエンド同値関係
コイコライザーの図
$`\xymatrix {
\boldsymbol{A} \ar@/^/[r]^{L} \ar@/_/[r]_{R}
& \boldsymbol{B}\ar@{.>}[r]^{?}
& \cdot
} \text{ where } L;? = R;?\In {\bf Set}`$
における $`\boldsymbol{A}, \boldsymbol{B}, L, R`$ は前節でハッキリしました。コイコライザーを作る手順は、
$`L, R`$ から定まる関係を同値関係にまで拡張して、その同値関係で商集合を作るのでした。
基本となる関係(それ自体は同値関係とは限らない)は次のように書けます。
$`\For (Z, y), (Z', y') \in \sum_{Z\in |\cat{C}|}P(Z,Z)\\
\quad (Z, y) \sim (Z', y') :\Iff\\
\qquad \exists (f, s)\in \sum_{f:X\to Y\in \mrm{Mor}(\cat{C})} P(Y, X).\\
\qquad\quad L(f, s) = (Z, y) \;\land\; R(f, s) = (Z', y')
`$
この条件を、左作業 $`L_f`$ と右作用 $`R_f`$ を使って集合圏のなかのストリング図で描けば次のようになります。
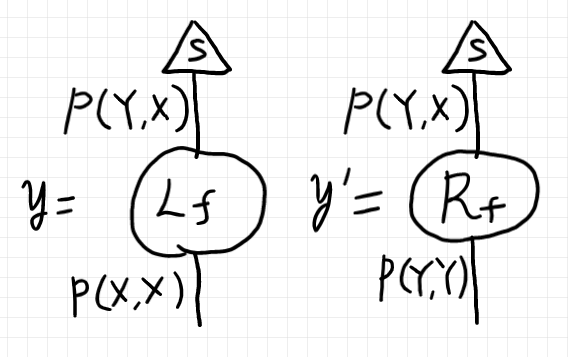
ノードをボックスに膨らませれば次の図になります。
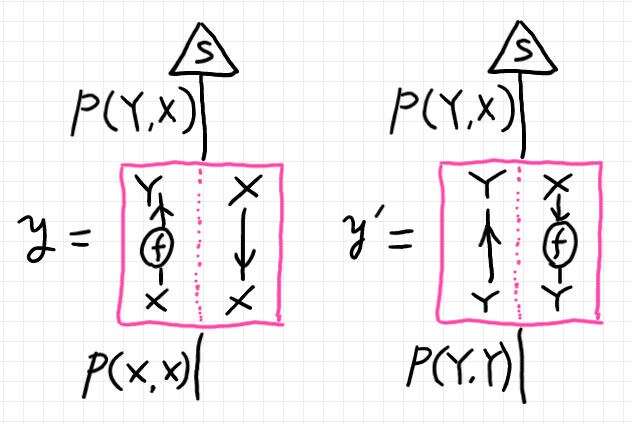
過去記事で描いた図(下)は、このことを表そうとした絵です。
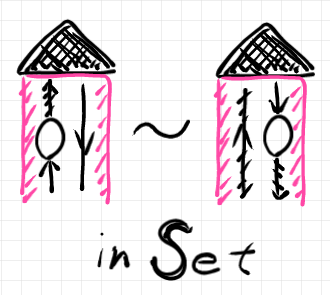
この記事の内容を念頭に「米田テンソル計算 1: 経緯と発想 // 関手ボックス」の短い説明を読んでもらえれば、簡潔(というか雑)ながらもコエンド同値関係の説明をしていることが分かるでしょう。
*1:既にコエンドを知っている人へのリマインドという位置づけなのでしょう、たぶん。
*2:カンフーの先生(映画のなかのブルース・リー)が弟子に教える場面でこの言葉を発しています。2012年に書いた記事「抽象的と具体的、自分の日本語が変で困った」参照。