記号の乱用〈記法の{乱用 | 濫用} | abuse of notation〉は、ものごとを分かりにくくして誤解と混乱のもとになります。しかし、非常に広く使われていて、使わないで済ますことが困難です。人間にとってだけではなく、プログラミング言語や証明支援系などのソフトウェアが記号の乱用を解釈・処理するのも難しい課題となっています。$`\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\In}{\text{ in } }
`$
内容:
記号の乱用の例と型クラス
記号の乱用の例を挙げます。
$`M = (M, *, e)`$ をモノイドとする。ここで、$`M`$ はモノイドの台集合、$`*`$ は二項演算、$`e`$ は単位元である。
文字〈一文字の名前〉 $`M`$ が、モノイド構造とその台集合〈underlying set〉の両方の意味で使われています。$`M`$ が出現したとき、モノイド構造なのか?その台集合なのか?は、文脈で判断します。
記号の乱用のソフトウェア的実装方式のひとつとして、型クラスがあります。僕は型クラスにはだいぶ不満をいだいてますが、今はその話は置いときます。最近よく話題にするLean 4(「プログラミング言語Lean 4の現状」参照)も型クラスを持っています。
Lean 4の型クラス・メカニズムでは、“記号の乱用の仕方”の情報をデータベース*1に保存しておいて、データベースを検索して曖昧な表現を解決〈resolve〉します。Lean 4の型クラス・メカニズムについては次の論文で解説されています。
- Title: Tabled Typeclass Resolution
- Authors: Daniel Selsam, Sebastian Ullrich, Leonardo de Moura
- Submitted: 13 Jan 2020 (v1), 21 Jan 2020 (v2)
- Pages: 18p
- URL: https://arxiv.org/abs/2001.04301
素朴な(あまり工夫しない)方法でデータベース検索をすると、検索・計算のコストが指数関数的に増大してしまうようです。以下のグラフ(上記論文)を見ると、Lean 4(青い線)以外の現存の処理系は複雑・大規模な検索には耐えられないようです。
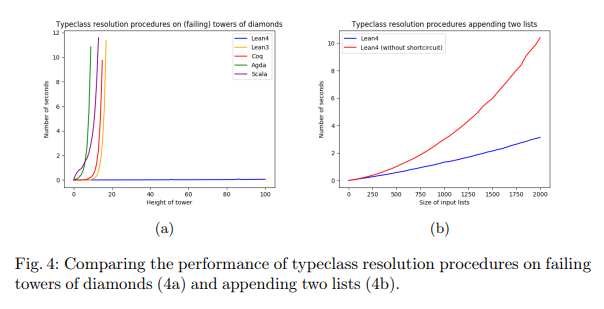
人間が、機械〈ソフトウェア〉より検索やパターンマッチングの能力が高いとも思えないので、記号の乱用を多用した記述を解釈することは、人間にも大きな負荷をかけるでしょう。ソフトウェアの曖昧性解決能力が上がるのはけっこうなことですが、人間には到底解釈できないような“超絶・記号の乱用”でも処理できてしまう、ってのはどうなんでしょうね? 乱用は乱用(よくない事)なので、その使用はほどほどにとどめたいところです*2。
付点半群の例
前節の例のモノイドは簡単な代数構造ですが、それでも事例としてはちょっと複雑なので、もっと簡単な付点半群を例にします。付点半群は次の指標〈signature〉で記述できます。
// 付点半群〈pointed semigroup〉
signature PtSemigroup {
sort U in Set // 台集合
operation op : U×U → U in Set // 二項演算
operation e : 1 → U in Set // 基点(単位元というわけではない)
// 法則は二項演算の結合法則のみ
law assoc : True → ∀(x, y, z∈U).( op(op(x, y), z) = op(x, op(y, z)) ) in Prop
}法則は、集合圏の2-射ではなくて、命題の圏 $`{\bf Prop}`$ の1-射(つまり証明)を要求する形で書いています。e はポインティング写像ですが、台集合の要素と同一視します。単位法則を要求してないので、e が単位元というわけではないです。
付点半群(という概念)を定義する指標には、4つの記号〈ラベル〉が登場します。
- U
- op
- e
- assoc
4つの記号のなかから幾つかを選ぶと、別な概念を定義することができます。例えば、U, e を選ぶと付点集合を定義できます。
// 付点集合〈pointed set〉
signature PtSet {
sort U in Set // 台集合
operation e : 1 → U in Set // 基点
}しかし、U, assoc を選ぶわけにはいきません。assoc が op を必要としているからです。U, op, assoc なら選べます。
指標に出現する記号の部分集合から定義される指標は、もとの指標が定義する概念の上位概念を定義します。下位概念じゃなくて上位概念です。もっとも、上か下かなんてのは恣意的に決めた比喩なんで無意味なんですけど、世間的な合意では「上位概念」です。
不点集合の上位概念を定義する記号の組み合わせには次があります。
- U, op, e, assoc : 付点半群(もとの概念)
- U, op, assoc : 半群
- U, op : マグマ
- U, e : 付点集合
- U : 集合
- (何もない) : voidな構造(ひとつだけ存在する)
もとの指標の記号〈ラベル〉達の部分集合から作られる指標を(もとの指標の)部分指標〈subsignature〉と呼びます。先に注意したように、部分指標はもとの概念の上位概念を定義します。一方、オブジェクト指向のサブクラス〈派生クラス | 導出クラス〉は下位概念を定義します。2006年の過去記事に書いています。
「サブ/スーパー」だの「上/下」などの言い方は、所詮はその場の思い付きによる比喩なので、違う人/違う場面では違う比喩になります。言い回しはまったく当てになりません。
相対指標と相対モデル
指標 $`\Sigma`$ に対して、そのモデル〈インスタンス | 実装〉の全体と、モデルのあいだの準同型写像達は圏を形成します。その圏を $`\mrm{Model}(\Sigma)`$ と書きます。今日はモデル達の圏の対象だけを考えるので、次のように定義します。
$`\quad \mrm{ModelCalss}(\Sigma) := |\mrm{Model}(\Sigma)|`$
例えば、
$`\quad \mrm{ModelCalss}(\text{PtSemigroup}) := |\mrm{Model}(\text{PtSemigroup})| = |{\bf PtSemigroup}|`$
ここで出てくる"Class"は、オブジェクト指向のクラスとも型クラスとも何の関係もなくて、大きいかも知れない集合(圏 $`{\bf SET}`$ の対象)という意味です。
指標 $`\Delta`$ が指標 $`\Sigma`$ の部分指標であることを $`\Delta \sqsubseteq \Sigma`$ と書きます。$`\Delta \sqsubseteq \Sigma`$ であるとき、忘却写像〈forgetful map〉が定義できます。
$`\quad \mrm{U}_{\Delta \sqsubseteq \Sigma} : \mrm{ModelCalss}(\Sigma) \to \mrm{ModelCalss}(\Delta) \In {\bf SET}`$
忘却写像は、構造の一部を捨て去って、より上位の(よりプアな)構造にする写像です。典型的な忘却写像は、構造の台集合だけを取り出す写像ですが、それに限りません。付点半群から付点集合にすることも、付点半群を半群にすることも忘却写像です。台集合さえ捨ててしまうと、唯一のvoidな構造になります。唯一のvoidな構造は、肉体を持たない精神だけの神様みたいな最上位概念です。しかし、それは全てを捨て去った無でもあるのです。色即是空 -- よく知らんけど。
$`\Delta \sqsubseteq \Sigma`$ であるような指標のペア $`(\Delta, \Sigma)`$ を相対指標〈relative signature〉、$`\mrm{U}_{\Delta \sqsubseteq \Sigma}(Y) = X`$ であるモデルのペア $`(X, Y)`$ を相対モデル〈relative model〉と呼びます。モデルをしばしばインスタンスとも呼ぶので、相対モデルは相対インスタンス〈relative instance〉と呼んでもいいでしょう。単にインスタンスと呼んでいるケースが一番多そうです。
相対モデル・データベースと検索
以下で述べるのは特定の実装の説明ではなくて、一般的な原理です。ここでは述べない他の方式もあります。また、今のところ人間しか解釈できない曖昧表現もあります。
記号の乱用を解釈するためのデータベースには、相対モデル〈so-called インスタンス〉を記録しておきます。実例を出しましょう。付点半群の指標は $`\mrm{PtSemigroup}`$ でした。単なる集合の指標は $`\mrm{Set}`$ とします。$`\mrm{Set}\sqsubseteq \mrm{PtSemigroup}`$ なので、次のような忘却写像があります。
$`\quad \mrm{U}_{\mrm{Set}\sqsubseteq \mrm{PtSemigroup}} : |{\bf PtSemigroup}| \to |{\bf Set}| \In {\bf SET}`$
これは、台集合以外捨てる写像で、典型的な忘却写像です。この忘却写像に対する相対モデルを考えます。自然数の集合 $`{\bf N}`$ に対して、台集合が $`{\bf N}`$ であるような付点半群 $`S`$ を取れば、$`({\bf N}, S)`$ は相対モデルになります。
$`{\bf N}`$ を台集合とする付点半群というと、通常の足し算や掛け算の半群構造と、単位元を基点に取りたくなります。が、そうである必要はありません。次のような付点半群を $`{\bf S}`$ と置きます。
- $`{\bf S}`$ の台集合は $`{\bf N}`$ 。
- $`{\bf S}`$ の二項演算は、右自明演算。つまり、$`\mrm{op}(x, y) = y`$ 。
- $`{\bf S}`$ の二項演算の基点 $`e`$ は、$`1\in {\bf N}`$ 。
- 右自明演算は結合法則を満たす(証明できる)。
$`({\bf N}, {\bf S})`$ は相対モデルになるので、これをデータベースに登録します。自然数の集合にはもともと固有名詞が付いてましたが、付点半群には特に呼び名を与えません。固有名詞の代わりに「$`{\bf N}`$ を台集合とする付点半群」という言い方で参照することにします。
「自然数の集合 $`{\bf N}`$」と「$`{\bf N}`$ を台集合とする付点半群」は別なものですが、「付点半群 $`{\bf N}`$」という表現が出てきたらデータベースを引いて $`{\bf S}`$ のことだと理解します。それが、記号の乱用/曖昧な参照の解決になります。
明白に「付点半群 $`{\bf N}`$」と書いてあるなら記号の乱用の解決は簡単ですが、$`{\bf N}`$ の存在が暗黙的な状況で、暗黙の $`{\bf N}`$ を $`{\bf S}`$ に置き換える操作は、文脈を精緻に解析しないといけないので複雑なアルゴリズムになります。記号の乱用が何段階にも使われていると、データベース検索も文脈解析も一筋縄ではいかなくて、パターンマッチングやトライ・アンド・エラーの技法を使うことになり、(工夫しないと)重い操作になります。
先の「$`{\bf N}`$ を台集合とする付点半群」の例では、わざと天邪鬼な相対モデルを出しましたが、通常は「$`{\bf N}`$ を台集合とする付点半群」に対して多くの人が連想するであろう“標準的な”相対モデルを登録するようにします。そうすれば、多くの人が自然な連想から理解できるだろう、ということです。
しかし、多くの人が連想する標準的な相対モデルが一意に決まるわけもなく、うまく連想できない事態も発生します。やはり乱用は乱用(よくない事)です。乱用に溺れて破綻しないように注意しましょう。