半グラフは、グラフの拡張概念で、辺の両端に頂点があることを要求しません。片側しか頂点がない辺、頂点と接続してない辺も認めます。
ツリーは、グラフのなかでも特によく使われるものです。ツリーを半グラフ・ベースで考えたらどうなるでしょうか? グラフのときとは様子が変わってきます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\bdry}{\partial }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\slt}{\mathrel{\dot{\lt}}}% successor lt
`$
内容:
半グラフ
以下は半グラフ〈semi-graph〉の例です。複数の半グラフではなくて1つの半グラフです。頂点〈vertex〉は裸の番号で識別し、辺〈edge〉は括弧付きの番号で識別しています。
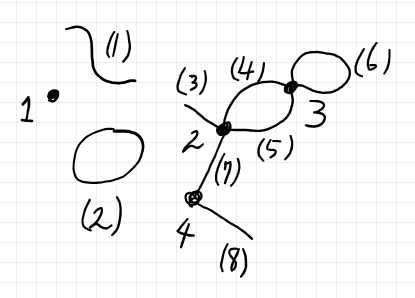
- 頂点 1 は、孤立頂点です。辺と接続していません。
- 辺 (1) は、無頂点辺です。頂点と接続していません。
- 辺 (2) は、無頂点ループ〈例外ループ〉です。
- 辺 (3)、(8) は外部辺〈開放辺〉です。片側だけ頂点と接続しています。
- 辺 (4)、(5)、(6)、(7) は内部辺です。両側で頂点と接続しています。
- 辺 (4)、(5) は、両端の頂点を共有します。多重辺と呼びます。
- 辺 (6) は、自己ループ辺です。両端が同一の頂点と接続しています。
- この半グラフは、4つの連結成分(繋がったかたまり)を持ちます。
半グラフについては、次の過去記事で説明しています。
半グラフには様々な定義があります。定義によって表現できない構成素もあります。例えば、よく使われているボリソフ/マニン方式の定義だと、無頂点辺と無頂点ループを表現できません。
次の節で述べる境界写像を使う方式では、無頂点ループと自己ループ辺が表現できません。ツリーを表現することが目的なので、ループを表現できなくても問題になりません。どうせツリーにはループがないので。
境界写像
[追記]注意: ここで述べる半グラフの定義は、「半グラフの様々な定義」で紹介したどの定義とも違います。半辺〈フラグ〉の概念を使わずにいきなり辺を定義しています。辺の境界写像は、非決定性写像として与えられます。[/追記]
以下、無頂点ループも自己ループ辺も持たない半グラフだけを考えます。例えば、次は前節の例から無頂点ループと自己ループ辺を取り除いたものです。
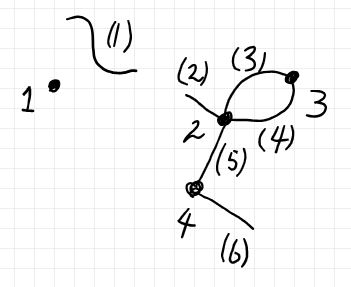
半グラフ(無頂点ループ・自己ループ辺は無し)の頂点の有限集合を $`V`$ 、辺の有限集合を $`E`$ とします。辺に、接続している頂点の集合を対応させる写像を $`\bdry`$ とします。この写像 $`\bdry`$ を境界写像〈boundary map〉と呼びます。
$`\quad \bdry : E \to \mrm{Pow}_{\le 2}(V) \In {\bf Set}`$
ここで、$`\mrm{Pow}_{\le 2}(V)`$ は $`V`$ のベキ集合ですが、要素の個数が2以下の部分集合だけを含むものです。つまり、辺 $`e`$ に対する写像 $`\bdry`$ の値 $`\bdry(e)`$ は、次のいずれかです。
- $`\bdry(e)`$ は空集合: $`\bdry(e) = \emptyset = \{\}`$
- $`\bdry(e)`$ は単元集合: とある頂点 $`v`$ があって、$`\bdry(e) = \{v\}`$
- $`\bdry(e)`$ はニ元集合: 異なる2つの頂点 $`v, w`$ があって、$`\bdry(e) = \{v, w\}`$
それぞれの場合を、次のように表現します。
- 辺 $`e`$ は、無頂点辺〈edge with no vertices | nodeless edge〉である。
- 辺 $`e`$ は、外部辺〈external edge | outer edge〉である。
- 辺 $`e`$ は、内部辺〈internal edge | inner edge〉である。
外部辺は開放辺〈open edge〉とも呼びます。無頂点辺を外部辺〈開放辺〉の仲間に入れるかどうかは人によりますが、この記事では、無頂点辺も特殊な外部辺とみなします。
頂点 $`v\in V`$ に対して、$`v`$ に接続している辺の集合は次のように書けます。
$`\quad \mrm{NbE}(v) := \{e\in E \mid v\in \bdry(e)\}`$
$`\mrm{NbE}(v)`$ を、頂点 $`v`$ の近傍辺集合〈set of neighbourhood edges〉と呼びます。近傍辺集合 $`\mrm{NbE}(v)`$ の基数(要素の個数)を、頂点 $`v`$ の次数〈degree〉または価数〈valency〉と呼びます。価数 0 の頂点は孤立した頂点です。
この記事で扱う半グラフ〈semi-graph〉をあらためて定義すれば、上記の集合・写像の3つ組 $`(V, E, \bdry)`$ のことです。絵に描くときは、$`V`$ の要素(有限個です)をドットで描いて、辺 $`e\in E`$ ごとの境界の値 $`\bdry(e)`$ を見て辺と頂点を接続して〈繋いで〉いきます。$`E`$ も有限集合なので、有限ステップで描き終わります。
開放ツリーの雰囲気
半グラフであって、ツリー〈木〉の形をしたものを開放ツリー〈open tree〉と呼びます。例えば、次の図は開放ツリーの例です。
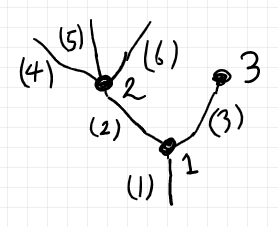
これは開放ツリーの定義にはなってなくて、単に気持ち・雰囲気を伝えただけです。
「開放〈open〉」を付けたのは、開放辺〈外部辺〉を持つかも知れないからです。開放辺を持つかも知れないグラフを開放グラフ〈open graph〉と呼んだのは、ディクソン/ダンカン/キッシンジャーの次の論文です。
- [DDA10-]
- Title: Open Graphs and Computational Reasoning
- Authors: Lucas Dixon, Ross Duncan, Aleks Kissinger
- Submitted: 22 Jul 2010
- Pages: 12p
- URL: https://arxiv.org/abs/1007.3794
この論文の手法は今回使いませんが、open XXX というネーミングだけ拝借します。
開放ツリーの形式的定義としては、ワイスの次の論文のアイディアを採用します。
- [Wei10-11]
- Title: From Operads to Dendroidal Sets
- Author: Ittay Weiss
- Submitted: 20 Dec 2010 (v1), 12 Jun 2011 (v3)
- Pages: 40p
- URL: https://arxiv.org/abs/1012.4315
半グラフの辺(頂点ではない)の集合に順序構造を考えることがワイスの着眼点です。ワイスはそもそも、頂点という概念はない状態で開放ツリーを定義しています。辺の集合しか考えないのです。しかし、これはちょっと分かりにくいので、前節で述べた半グラフを前提にすることにします。
辺の集合に入る順序関係が、ツリーをツリーたらしめるキモになるのですが、その順序構造を次節で説明します。
ツリー順序
$`X`$ を有限集合として、$`(X, \le)`$ を順序集合だとします。$`\lt, \slt`$ という関係を次のように定義します。
$`\text{For }x, y\in X\\
\quad x \lt y \;:\Iff\; x \le y \land x \ne y\\
\quad x \slt y \;:\Iff\; x \lt y \land \forall t\in X.(\, x\le t \le y \Imp (x = t \lor y = t)\,)
`$
$`x \slt y`$ の意味は、$`y`$ は $`x`$ より真に大きくて、$`x, y`$ の中間にその他の要素がないことです。別な言い方をすると、$`y`$ は $`x`$ の直後の要素(後者ともいいます)です。しかし、全順序〈線形順序〉とは限らないので、直後の要素が1つだけとは限りません。直後の要素が無いときも、複数あるときもあります。
$`x \slt y`$ のとき、次の言い方をします。
- $`x`$ は、$`y`$ の親〈parent〉である。
- $`y`$ は、$`x`$ の子〈child〉である。
つまり、関係 $`\slt`$ は親子関係ということです。順序 $`\le`$ の最小元があれば、それは、他のすべての要素の祖先ということになります。
さて、台が有限である順序集合 $`(X, \le)`$ がツリー順序集合〈tree ordered set〉であるとは次のことです。
- 最小元が存在する。
- 最小元以外の要素の親(直前の要素)はただ1つだけ存在する*1。
この定義だと、空集合はツリー順序集合になれません(最小元が存在しないので)。最小元以外の親は一意に確定しますが、子が一意とは限りません。
$`(X, \le)`$ がツリー順序集合のとき、最小元をルート〈root | 根〉と呼びます。
台が有限である順序集合 $`(X, \le)`$ がツリー順序集合のとき、最小元であるルート $`r`$ を添えて $`(X, \le, r)`$ と書くことにします。ツリー順序集合では、親(直前の要素)を対応させる関数 $`\mrm{parent}`$ を定義できます。
$`\quad \mrm{parent} : X\setminus\{r\} \to X \In {\bf Set}`$
$`\mrm{parent}`$ の逆像関数(逆関数ではない)として、$`\mrm{Children}`$ を定義できます。
$`\quad \mrm{Children} := \mrm{parent}^{-1}\; : X \to \mrm{Pow}(X\setminus\{r\}) \In {\bf Set}
`$
開放ツリーの定義
この記事における開放ツリーとは、半グラフ・ベースの根付きツリー〈rooted tree〉のことです。半グラフ・ベースのツリーの定義として、その幾何実現〈geometric realization〉を使う方法があります。「亜群をベースとする圏類似構造: コステロの事例」で紹介したコステロの論文ではそのような方法でツリーを定義しています。
- [Cos04-04]
- Title: The A-infinity operad and the moduli space of curves
- Author: Kevin Costello
- Submitted: 2 Feb 2004 (v1), 15 Sep 2004 (v2)
- Pages: 14p
- URL: https://arxiv.org/abs/math/0402015
幾何実現が連結(連結成分が1つ)で、サイクルを持たないとき、半グラフはツリー〈tree〉だと呼びます。この意味でのツリーは辺に向きがなく、ルートも持ちません。例えば、次の図はツリーです。
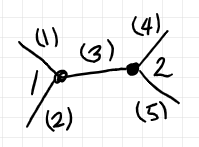
ルート辺(ルート頂点ではない!)として外部辺の1つを指定したツリーを根付きツリー〈rooted tree〉と呼びます。上の図のツリーの辺 (5) をルートだと指定すると根付きツリーになります。ルート辺が下に来るようにレイアウトすると次の図になります。
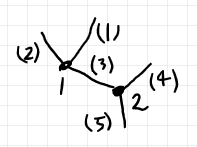
ここでは、幾何実現に頼らず、組み合わせ的に半グラフ・ベースの根付きツリーを定義します。
半グラフ $`(V, E, \bdry)`$ が開放ツリー〈open tree〉であるとは、次のことです。
- 辺の集合(頂点の集合ではない)を台としたツリー順序集合 $`(E, \le, r)`$ がある。ルート辺 $`r`$ は外部辺(無頂点辺でもよい)である。
- 任意の頂点に“すぐ下の辺”を対応させる写像 $`\mrm{under}`$ がある(詳細後述)。
一番目の条件に出てくるツリー順序集合の構造と写像 $`\mrm{under}`$ を組み込むと、開放ツリーは $`(V, E, \bdry, \le, r, \mrm{under})`$ と書けます。$`(E, \le, r)`$ はツリー順序集合で、$`r\ \in E`$ は1つの頂点とだけ接続しているか、または頂点とまったく接続していません(無頂点辺)。
前々節の開放ツリーの絵から、辺だけを抜き取ると次のようです。頂点があったところは点線で示しています。
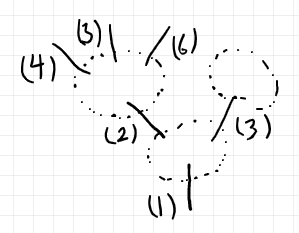
辺 (1) が一番小さくて、上に行くほど大きくなるという順序を考えると、辺達のあいだのツリー順序になります。一方、祖先・子孫の順序では、下にいくほど祖先、上に行くほど子孫になります。この例の $`\mrm{parent}`$ 関数を示すと:
$`\quad \mrm{parent}(\,\text{(4)}\,) = \text{(2)}\\
\quad \mrm{parent}(\,\text{(3)}\,) = \text{(2)}\\
\quad \mrm{parent}(\,\text{(6)}\,) = \text{(2)}\\
\quad \mrm{parent}(\,\text{(2)}\,) = \text{(1)}\\
\quad \mrm{parent}(\,\text{(3)}\,) = \text{(1)}
`$
写像 $`\mrm{under}`$ は次の条件を満たします*2。
$`\quad \mrm{under} : V \to E \In {\bf Set}\\
\:\\
\quad \forall v \in V. \{\mrm{under}(v)\} \cup \mrm{Children}(\mrm{under}(v)) = \mrm{NbE}(v)
`$
この条件を日本語で書けば:
- 頂点 $`v`$ の“すぐ下の辺”と、“すぐ下の辺”の子の辺達が、$`v`$ の近傍辺集合を構成する。
順序構造と“すぐ下の辺”(写像 $`\mrm{under}`$)を備えた半グラフは、我々が直感的に思っている“ツリー”を表現しています。特に重要なことは、ツリーの各部に、地面からの高さが定義できることです。
高さ関数
$`(V, E, \bdry, \le, r, \mrm{under})`$ を開放ツリーとします。辺の集合 $`E`$ 上に、高さ関数 $`\mrm{height}`$ を定義しましょう。
$`\quad \mrm{height} : E \to {\bf N} \In {\bf Set}`$
まず、ルート辺 $`r`$ の高さは 0 だとします。
$`\quad \mrm{height}(r) := 0 `$
ルート辺だけからなる(頂点はなし)半グラフも開放ツリーと認めますが、その場合は高さ関数の定義は完了です。一般には、ルート辺以外の辺もあるでしょうから、まだ定義が続きます。
ルート辺のすぐ上の辺は $`\mrm{Children}(r)`$ で列挙できるので、これらには 高さ 1 を与えます。以下順次、「親の高さ + 1」の値を与えていけばいいわけです。
が、ほんとにこの方法で矛盾なく辺の高さを定義できるのでしょうか? 上記の方法は、“ルート辺から当該の辺に至るパスの長さ” 引く 1 として高さを与えています。もし、“ルート辺から当該の辺に至るパス”が2本以上あると、それらのパスの長さが食い違う可能性が出てきます。「パスは一本しかないはずだ」と思うのですが、ほんとうでしょうか?
おおよその議論は; ルート辺 $`r`$ から当該の辺 $`e`$ に至る異なる2本のパスがあったと仮定すると、次のような辺 $`x, y, z`$ が存在することが言えます。
$`\quad x \ne y\\
\quad x \slt z\\
\quad y \slt z
`$
これは、「親が唯一に決まる」という開放ツリーの条件(元を正せばツリー順序集合の条件)に反するので、異なる2本のパスなんてない、ってことになります。
開放ツリーの下部構造であるツリー順序集合の利用者としては、ツリー順序集合の上で「再帰的関数定義をしてよい」と思っておけばいいでしょう。
$`(X, \le, r)`$ がツリー順序集合であるとき、$`f:X \to Y`$ を定義する際に、次の手順で $`f`$ を定義してかまいません。
- $`f(r)`$ の値を決める。
- $`x \in X`$ に対して、$`x`$ の先祖達に対する $`f`$ の値を使って $`f(x)`$ の値を計算する方法を決める。
特に、$`f(x)`$ の値が $`f(\mrm{parent}(x))`$ の値から決まるなら、($`f(r)`$ の値とともに)$`f`$ 全体を定義したことになります。
[/追記]
次に、頂点の集合 $`V`$ 上にも、高さ関数 $`\mrm{height}`$ (名前をオーバーロードする)を定義しましょう。
ルート辺の“すぐ上の頂点”があれば、それに高さ 1 を与えます。その他の頂点に関しても、“すぐ下の辺”の高さに 1 を足して頂点の高さとします。“すぐ下の辺”は写像 $`\mrm{under}`$ で一意に決まります。
以上の手順で、すべての辺/すべての頂点に高さを与えることができて、関数 $`\mrm{height}`$ は次のような関数になります。
$`\quad \mrm{height} : (E + V) \to {\bf N} \In {\bf Set}`$
関数 $`\mrm{height}`$ の最大値を開放ツリーの高さ〈height〉とします。開放ツリーの高さは、辺/頂点の高さと混同しないで区別してください。
以下の図は、(ひとつのツリーではなくて)5本の開放ツリーです。
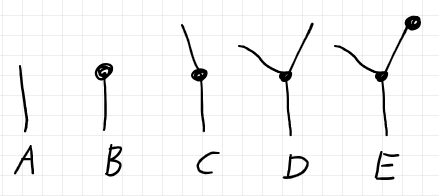
それぞれの高さは次のようになります。
- 開放ツリー A の高さは、0 である。
- 開放ツリー B の高さは、1 である。
- 開放ツリー C の高さは、1 である。
- 開放ツリー D の高さは、1 である。
- 開放ツリー E の高さは、2 である。
兄弟順序付き開放ツリー
$`(V, E, \bdry, \le, r, \mrm{under})`$ を開放ツリーとします。親子関係/祖先・子孫関係とは別に、兄弟のあいだの“長幼の序”を与える順序を持つとき、兄弟順序付き開放ツリー〈sibling ordered open tree〉と呼びます。単に順序付き開放ツリー〈ordered open tree〉と言ったときも、兄弟のあいだの順序があることを意味します。
$`e, f\in E`$ に対して、「兄弟である」という意味の述語 $`\mrm{areSiblings}`$ を定義します。
$`\quad \mrm{areSiblings}(e, f) :\Iff \mrm{parent}(e) = \mrm{parent}(f)`$
辺の集合 $`E`$ 上の関係 $`\sqsubseteq`$ が兄弟順序〈sibling order〉だとは、次を満たすことです。
- $`\sqsubseteq`$ は順序関係である。
- $`f \sqsubseteq g \Imp \mrm{areSiblings}(f, g)`$
- $`\mrm{areSiblings}(f, g) \Imp f \sqsubseteq g \lor g \sqsubseteq f`$
これは、順序関係 $`\sqsubseteq`$ が、兄弟のあいだでは全順序〈線形順序〉関係になると言っています。兄弟ではない二辺 $`f, g`$ に関しては、$`f\sqsubseteq g`$ も $`g\sqsubseteq f`$ も成立しません(比較不能)。
開放ツリーに兄弟順序があれば、兄弟である辺の集合をリストとして一意的に表示できます。
開放ツリーの切り分け分解
バーガー/カウフマンは、次の論文内でグラフの「解剖〈dissection〉」という言葉を使ってましたが、意訳して「切り分け分解」とします。
- [BK22-]
- Title: Trees, graphs and aggregates: a categorical perspective on combinatorial surface topology, geometry, and algebra
- Authors: Clemens Berger, Ralph M. Kaufmann
- Submitted: 25 Jan 2022
- Pages: 48p
- URL: https://arxiv.org/abs/2201.10537
切り分け分解〈dissection〉とは、与えられた半グラフの内部辺にハサミを入れて、単純なグラフの集まりにすることです。コステロの半グラフ圏でも、グラフ置換射の域を求めるために切り分け分解をしてます。
開放ツリーを切り分け分解すると、単にパランパランの半グラフに分解するのではなくて、高さごとのグルーピングができます。
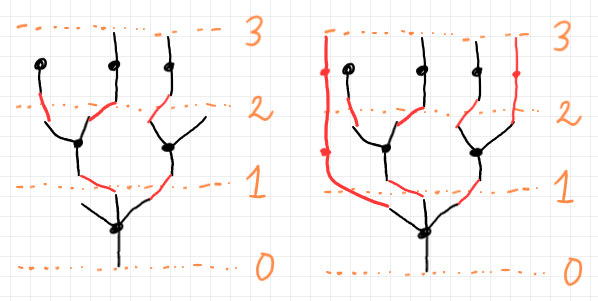
開放ツリーの切り分け分解を、絵を使って大雑把に説明します。以下のように、高さレベルのレベル線を引きます。内部辺がレベル線と交差した位置が切り分ける(辺を切断する)場所です。赤いバッテンが描いてあります。外部辺は切り分けに関係しません。
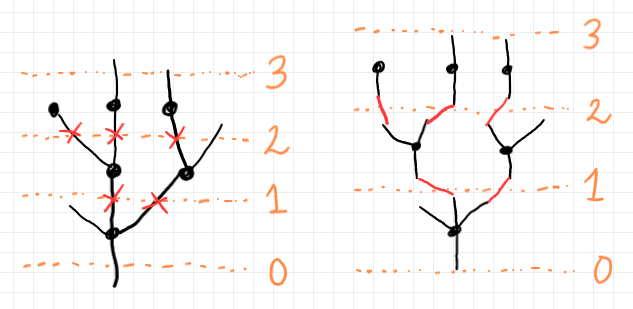
上図の右側は切り分け分解した後です。一本のツリーが、6本の小さいツリー(カローラ〈corolla〉と呼ぶ)に分けられました。赤い線は、もとのツリーを再現するためのリンク情報です。リンクで結ばれた辺を接ぎ木〈grafting〉で繋ぐともとのツリーができます。
開放ツリーが兄弟順序付きで、恒等射に相当するダミーのカローラが使えるときは、切り分け分解と再現がもっと容易になります。赤で描いたダミーのカローラを追加すると、横に並んだカローラのリストを単純に積み上げるだけでもとのツリーを再現できます。
おわりに
圏の射を図示するために、アローやパスが使われます。同様に、オペラッド〈複圏〉のオペレーション〈複射〉の図示にはツリーが必要です。この記事で定義した開放ツリーと兄弟順序付き開放ツリーは、オペレーション〈複射〉の組み合わせ的議論や視覚化の基礎となるものです。