データベースに関する説明では、一見して理論的に見えても、その実、内容が曖昧だったり残念だったりすることがあります。例えば、数年前に次の記事を書きました。
最近、ER図に出てくる“カラスの足”記法がよく分からないので調べてみたのですが、説明読んでも結局分からないままですわ。なにあれ?$`\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }
\newcommand{\For}{\Keyword{For }}
\newcommand{\Define}{\Keyword{Define }}
\newcommand{\IsA}{\Keyword{ is-a }}
\newcommand{\Is}{\Keyword{ is }}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\hyp}{\text{-}}
\newcommand{\Iff}{\Leftrightarrow}
`$
内容:
続き:
“カラスの足”記法
“カラスの足”記法〈crow's foot notation〉とは、例えば、下の図の左右の箱を結ぶ線に付いている飾りのようなものです。
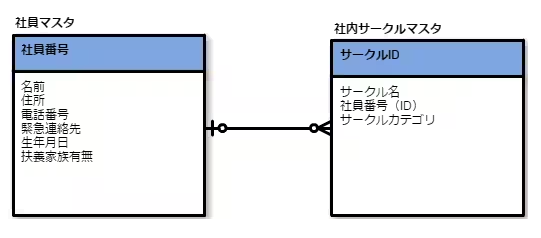
この図は、「若手プログラマー必読!5分で理解できるER図の書き方5ステップ」(別URLもあるようです)にあったものです。
左右の箱は、モノの種類なり集合なりを表していて、線は関係〈関連〉を表します。で、関係付けられているモノの個数を表すのが“カラスの足”のような記号で、「若手プログラマー必読!5分で理解できるER図の書き方5ステップ」(以下、『5分で理解できる』として参照)にあった説明を画像コピーすると:

これらの記号に対する適当な文字がないので、「0」「1」「<」で代用します。「<」では3本指の“カラスの足”っぽくないのですが、ご容赦ください。
『5分で理解できる』には6つの例がありますが、代替記法で6つの例を書けば次のようです。
- 1対1の関係: A 1----1 B
- 1対多の関係(あいまいな表現): A ----< B
- 1対0以上の関係: A 1----0< B
- 1対1以上の関係: A 1----1< B
- 多対多の関係: A >0----0< B
- 0または1対多の関係: A 1,0---0< B
6つの例に付いている説明の一部を引用すると(表記のゆれがありますが、そのまま引用します):
- 「1対1の関係」であることを表現している例です。
- 「1対多という関係は決まっているが、それ以上は決まっていない」という、データベース設計の初期段階の時に使います。
- 「1対0以上の関係」であることを表現している例です。「1対多」の関係性をより詳細に表現しています。
- 「1対1以上の関係」であることを表現している例です。「1対多」の関係性をより詳細に表現しています。
- 「多対多の関係」であることを表現している例です。「多対多の関係」でも、「0以上」「1以上」「0以上1以上どちらも表現しない(あいまい)」という表現が可能です。
- 「0または1対多の関係」であることを表現しています。上述の「多対多」の例との違いは、[檜山注: 社員とサークルのあいだの所属関係の例で] 社員は0以上の複数サークルに所属できるが、1つのサークルに所属できる社員は0か1名になります。[檜山注: そんなサークルある? 架空の例だからまーいいけど]
「多」ってなに?
『5分で理解できる』から次の3つの例を考えてみましょう。
- 1対多の関係(あいまいな表現): A ----< B
- 1対0以上の関係: A 1----0< B
- 1対1以上の関係: A 1----1< B
Aに属するモノを1つ選ぶと、それに関係付けられる、Bに属するモノがたくさんあるってことでしょう。「たくさん」を“ちゃんと”言うと「多 --<」「0以上 --0<」「1以上 --1<」となる、と。ウーン、ほんとに“ちゃんと”したのかぁ?
「--<」に対して「あいまいな表現」と言っており、「--0<」「--1<」は「「1対多」の関係性をより詳細に表現しています。」と言ったりしているんで、「--0<」は「--<」より精密な情報を提供している認識のようですが、ほんとにそうかなぁ??
日本語だから曖昧なのかと思ったら、英語でも同様な曖昧さでした。
- --0 Zero
- --1 One
- --< Many
- --0,1 Zero or One
- --0< Zero or Many
- --1,1 Only One
- --1< One or Many
いずれにしても、自然言語(日本語や英語)で議論していてはサッパリ埒が明かないですね。
関係と非決定性関数
$`A, B`$ を集合として、これらの集合のあいだの関係(二項関係だけを扱います)とは、直積集合の部分集合のことです。つまり、
$`\quad R \text{ は } A, B \text{ のあいだの関係}\\
\Iff R \subseteq A\times B\\
\Iff R \in \mrm{Pow}(A\times B)
`$
$`\mrm{Pow}(\hyp)`$ はベキ集合〈power set〉を表します。
一方、$`A, B`$ のあいだの〈$`A`$ から $`B`$ への〉非決定性関数〈非決定性写像〉*1とは次のようなものです。
$`\quad F \text{ は } A, B\text{ のあいだの非決定性関数}\\
\Iff F : A \to \mrm{Pow}(B) \:\text{ 関数}
`$
$`A, B`$ のあいだのすべての関係の集合を $`\mrm{Rel}(A, B)`$ 、$`A, B`$ のあいだのすべての非決定性関数の集合を $`\mrm{NDFun}(A, B)`$(NDFun = non-deterministic function)とします。これら2つの集合は同型です。つまり、
$`\quad \mrm{Rel}(A, B) \cong \mrm{NDFun}(A, B)`$
この同型を与える写像〈関数〉を書き出すと:
$`\mrm{ndf} : \mrm{Rel}(A, B) \to \mrm{NDFun}(A, B)\\
\quad \For R \in \mrm{Rel}(A, B)\\
\quad \Define \mrm{ndf}(R) := \lambda\, x\in A. \{y \in B\mid (x, y)\in R \}
`$
$`\mrm{rel} : \mrm{NDFun}(A, B) \to \mrm{Rel}(A, B) \\
\quad \For F \in \mrm{NDFun}(A, B)\\
\quad \Define \mrm{rel}(F) := \{ (x, y) \in A\times B \mid y \in F(x) \}
`$
次が成立します。
$`\For R \in \mrm{Rel}(A, B)\\
\quad \mrm{rel}(\mrm{ndf}(R)) = R\\
\For F \in \mrm{NDFun}(A, B)\\
\quad \mrm{ndf}(\mrm{rel}(F)) = F
`$
関係 $`R\in \mrm{Rel}(A, B)`$ に対応する非決定性関数 $`\mrm{ndf}(R)\in \mrm{NDFun}(A, B)`$ も、同じく $`R`$ と書いてしまうことにします。すると、次が成立します。
$`\For x \in A, y\in B\\
\quad (x, y) \in R \Iff y \in R(x)
`$
関係 $`R \in \mrm{Rel}(A, B)`$ の転置〈transpose〉を $`R^\mrm{T}\in \mrm{Rel}(B, A)`$ と書くことにします。転置の定義は:
$`\For x \in A, y\in B\\
\quad (y, x) \in R^\mrm{T} :\Iff (x, y) \in R
`$
非決定性関数としての転置の定義は:
$`\For y\in B\\
\quad R^\mrm{T}(y) := \{ x \in A\mid y \in R(x) \}
`$
関係のカーディナリティの制約
関係/非決定性関数の仕様記述として、関数〈写像〉と同様に、矢印の左右に域〈domain〉と余域〈codomain〉を書きます。域と余域の情報はプロファイルと呼びます。プロファイルの書き方を同じにすると、関係/関数/非決定性関数の区別が付かなくなるので、次のように「それが何であるか」を記入することにします。
$`\quad f :A \to B \IsA \text{function}\\
\quad R:A \to B \IsA \text{relation}\\
\quad F: A \to B \IsA \text{non-det function}
`$
もっとも、前節で約束したように、我々は関係と非決定性関数を同じ名前で呼んでしまうので、次のようなことになります。
$`\quad R:A \to B \IsA \text{relation}\\
\quad R: A \to B \IsA \text{non-det function}
`$
関係と非決定性関数をあまり区別しない方針です。
さて、“カラスの足”記法は、関係〈関連〉のカーディナリティ〈多重度〉(の制約)を表すのですが、『5分で理解できる』の定義(?)は:
「カーディナリティ」とは、「1対1」「1対多」「多対多」など、リレーションの詳細を表現する記号のことです。「0以上」や「0または1」といったことも表現することができます。
これだけです。他の記事も見たけど似たりよったりで、ちょっと何言ってるかわかんない((c)サンドウィッチマン)。
「正確な定義を探せ」と言われそうですが、なかなか見つからないので、「たぶんこんな意味なんだろう」を述べます。まず、考える非決定性関数 $`R:A \to B`$ に次の条件を付けます*2。
$`\quad \forall x\in A.(\, R(x) \text{ は有限集合} \,)`$
この条件を日本語で書けば:
集合 $`A`$ の任意の要素 $`x`$ に対して、非決定性関数 $`R`$ の値である集合 $`R(x)`$ は有限集合である。
すると、$`\mrm{card}(R(x))`$ は自然数として意味を持ちます。今出てきた $`\mrm{card}`$ は有限集合のカーディナリティ〈基数〉です。これは、有限集合の個数を勘定するだけなのでハッキリした意味を持ちます。$`n, m\in {\bf N},\; n \le m`$ に対して、以下の命題も意味を持ちます。
$`\quad n \le \mrm{card}(R(x)) \le m`$
便宜上の無限大 $`\infty`$ を導入すれば、次も意味を持ちます。
$`\quad n \le \mrm{card}(R(x)) \lt \infty`$
これは、$`\mrm{card}(R(x))`$ はいくら大きくなってもいいということで、上限は無条件になります。
カーディナリティの記号は線の右側だけに付けてもいいようなので(下図、「ER図(Entity Relationship Diagram)」より)、右側のカーディナリティ記号の意味を考えます。
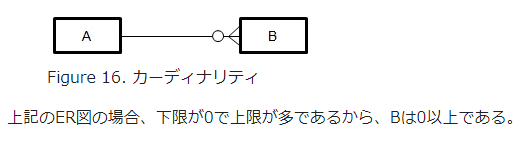
関係のカーディナリティを制約するとは、$`A`$ 全体(すべての要素)において $`\mrm{card}(R(x))`$ に条件を付けることでしょう。全体的な条件は次のように書けます。
$`\quad \forall x\in A.\, n \le \mrm{card}(R(x)) \le m`$
日本語で書けば:
集合 $`A`$ の任意の要素 $`x`$ に対して、集合 $`R(x)`$ のカーディナリティは $`n`$ 以上 $`m`$ 以下である。
上限が無条件なら、
$`\quad \forall x\in A.\, n \le \mrm{card}(R(x)) \lt \infty`$
日本語で書けば:
集合 $`A`$ の任意の要素 $`x`$ に対して、集合 $`R(x)`$ のカーディナリティは $`n`$ 以上である。
「多」について考えてみよう
次のようにカーディナリティの記号〈“カラスの足”〉が付いた関係を考えます。
- A ---- B
- A ----< B
- A ----0< B
- A ----1< B
1番は無条件です。カーディナリティが無条件とは、「0以上無限大未満」と同じことですから、論理式で書けば:
$`\quad \forall x\in A.\, 0 \le \mrm{card}(R(x)) \lt \infty`$
2番は「多〈Many〉」です。意味不明の「多〈Many〉」です。「0以上」「1以上」が「--0<」「--1<」なので、ひょっとして「多」は「2以上」ってこと? いやいや、それはない。『5分で理解できる』には「関係性をより詳細に表現」とあるので、「--0<」「--1<」のほうが情報が精密なはず。つまりは、「--<」はより漠然としているはず。‥‥ って、それって無条件のことじゃないの。
$`\quad \forall x\in A.\, 0 \le \mrm{card}(R(x)) \lt \infty`$
3番は明白に「0以上」です。つまり、
$`\quad \forall x\in A.\, 0 \le \mrm{card}(R(x)) \lt \infty`$
アリッ? 1番、2番、3番は全部同じになってしまった。4番は明白に「1以上」だから、
$`\quad \forall x\in A.\, 1 \le \mrm{card}(R(x)) \lt \infty`$
僕がハナから勘違いしている可能性もありますが、前節の解釈をとると、1番、2番、3番は同じで区別する意味はありません。
『5分で理解できる』に、「--<」は「データベース設計の初期段階の時に使います。」とあり、「--0<」は「より詳細に表現」とのことなので、カーディナリティ記号〈“カラスの足”〉って、気持ちを伝える記号なのかな? 例えば(あくまで架空の例え話)
| カーディナリティ記号 | 気持ち |
|---|---|
| -- (記号無し) | 何も考えてない |
| --< | あまり考えてない |
| --0< | 考えた結果こうなった |
まさかねぇ。
左側のカーディナリティ記号
左側のカーディナリティ記号は、関係〈非決定性写像〉の向きを逆にして考えればいいでしょう(たぶんだけど)。つまり、$`R`$ の代わりにその転置 $`R^\mrm{T}`$ を考えるのです。左右にカーディナリティ記号がついていれば、左側の条件と右側の条件の論理ANDを取ればいいでしょう(たぶんだけど)。
次の3つを考えてみます。
- A 1---- B
- A 1----0< B
- A 1----1< B
1番は次の条件を表しています。
$`\quad \forall y\in B.\, \mrm{card}(R^\mrm{T}(y)) = 1`$
$`R^\mrm{T}(y)`$ の定義で展開すれば:
$`\quad \forall y\in B.\, \mrm{card}( \{x\in A\mid y \in R(x) \} ) = 1`$
あるいは、$`R`$ を関係(直積集合の部分集合)とみなすならば:
$`\quad \forall y\in B.\, \mrm{card}( \{ (x, y)\in A\times B \mid (x, y) \in R \} ) = 1`$
日本語で書けば:
集合 $`B`$ の任意の要素 $`y`$ に対して、$`(x, y) \in R`$ となるような $`(x, y)`$ はただ1つだけ存在する。
これは $`y`$ を決めると $`(x, y)`$ が、したがって $`x`$ がただ1つだけ決まることです。言い方を変えると、$`B \to A`$ の方向の関数があることです。このことは次のように書けます。
$`\quad R^\mrm{T} : B \to A \IsA \text{function}`$
前節で述べた僕の憶測が正しいなら、「--0< B」は何の条件も課してないので、2番と1番は同じです。
3番は次の2つの条件を課します。
$`\quad \forall y\in B.\, \mrm{card}(R^\mrm{T}(y)) = 1\\
\quad \forall x\in A.\, 1 \le \mrm{card}(R(x))
`$
論理式を少し変形して、それを日本語で書けば:
集合 $`B`$ の任意の要素 $`y`$ に対して、$`(x, y) \in R`$ となるような $`(x, y)`$ はただ1つだけ存在する。
集合 $`A`$ の任意の要素 $`x`$ に対して、$`(x, y) \in R`$ となるような $`(x, y)`$ は存在する。
$`S := R^\mrm{T}`$ と置くと、$`S:B \to A`$ は関数(より正確には、関数とみなせる関係)になります。すると、もとの関係(あるいは非決定性関数) $`R`$ は、関数 $`S`$ と逆向きの対応となります。これは、関数 $`S`$ の逆像対応です。2番の条件は、「$`S`$ の各点での逆像が空でない」ということです。言い換えれば、「$`S`$ は全射である」ことです。
先の2つの条件は、次のように言っても同じです。
関係 $`R`$ の転置(逆向きの対応) $`S := R^\mrm{T}`$ は、関数とみなしてよい。
$`S`$ は、関数として全射である。
関係/非決定性関数の性質の記述
関係と非決定性関数は区別しないことにして、単葉〈たんよう | univalent | 一価〉、全域〈total〉、一意的〈unique〉という性質を定義しましょう。
$`\For R \IsA \text{relation / non-det function}\\
\Define R \Is \text{univalent} :\Iff
\forall x\in A.\, \mrm{card}(R(x)) \le 1\\
%
\Define R \Is \text{total} :\Iff
\forall x\in A.\, 1 \le \mrm{card}(R(x))\\
%
\Define R \Is \text{unique} :\Iff
\forall x\in A.\, \mrm{card}(R(x)) = 1
`$
次のことが言えます。
- $`R`$ が単葉かつ全域ならば一意である。
- $`R`$ が一意的なら関数(とみなしてよい関係)である。
- したがって、$`R`$ が単葉かつ全域ならば関数である。
- $`R`$ が単葉なら部分関数(未定義を許す関数 partial function)である。
カーディナリティ記号を使うと、単葉、全域、一意的は次のように書けます。
- A ----0,1 B ⇔ 関係は単葉である ⇔ 関係は部分関数である
- A ----1< B ⇔ 関係は全域である
- A ----1 B ⇔ 関係は一意的である ⇔ 関係は関数である
また、次の事実があります。
- 転置(逆向きの対応)が単葉である関数は単射である。
- 転置(逆向きの対応)が全域である関数は全射である。
- 転置(逆向きの対応)が単葉かつ全域である関数は全単射(可逆な関数)である。
これらのことを、カーディナリティ記号を使って書くと次のようになります。
- A 1,0----1 B ⇔ 関係は単射な関数である
- A >1----1 B ⇔ 関係は全射な関数である
- A 1----1 B ⇔ 関係は全単射な関数である ⇔ 関係は可逆な関数である
おわりに
この記事は、カーディナリティ記号〈“カラスの足”〉に関する解説を3つほど読んでみて、あまりに曖昧・意味不明なことにイラッとして、それ以上調べもせずに憶測に基づいて書いたものです。よって、「正式な定義はそうじゃない」という事態もあり得ます。
とはいえ、この記事に書いたカーディナリティ記号の使い方は悪くはないでしょう。「0〈Zero〉」「1〈One〉」「<〈Many〉」の組み合わせで、関係/非決定性写像の次の性質を表現できます。
- 単葉
- 全域
- 一意的(単葉かつ全域)
- 転置(逆向きの対応)が単葉
- 転置(逆向きの対応)が全域
- 転置(逆向きの対応)が一意的
これらの性質は実際重要なものだし、図に注釈したいことも多いでしょう。カーディナリティ記号はその目的で使うんじゃないのかな(知らんけど)。
続きがあります。