「米田埋め込みの書き方(色々ありすぎ)」において、米田埋め込みの記法がたくさんあることを紹介しました。別名/別記法の氾濫は、鬱陶しくて面倒な事ですが、メリットもあります。それは、用途・場面に応じて適切な呼び名と記法が選べることです。
今言った「適切さ」は、メンタル/エモーショナル、あるいは認知的な「適切さ」です。だって、別名/別記法の指す対象物〈denotation〉は同一なので、「何を指すか」に違いは無いのですから。
もうひとつ、記法には機能性・効率性があります。例えば、「視認性の良し悪し」「誤解されるリスクの大小」「短さ・簡潔さ」などの評価基準があります。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\hyp}{\text{-}}
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\In}{\text{ in } }
\newcommand{\On}{\text{ on } }
\newcommand{\id}{\mathrm{id} }
`$
この記事で話題にするのは、外部ホム関手の書き方に対する、認知的な適切さや機能性・効率性です。僕は、圏 $`\cat{C}`$ の外部ホム関手 $`\mrm{Hom}_{\cat{C}} :\cat{C}^\mrm{op}\times \cat{C} \to {\bf Set}`$ の射パートを $`(f, g)\mapsto g^f`$ と書くことがあります。これは、「短さ・簡潔さ」は申し分ないのですが、「誤解されるリスク」は大きく、「メンタルな違和感・抵抗感」の原因にもなりそうです。
なので、$`g^f`$ の代替記法を出します。幾つかの記法を見ることで、「別にどれでもいいや」という“悟り”に至るかも知れません。
内容:
米田の補題の補題
「米田の補題とストリング図」の最後のほうで、「米田の補題の補題」として次の絵図等式〈{graphical | pictorial} equation〉を挙げました。
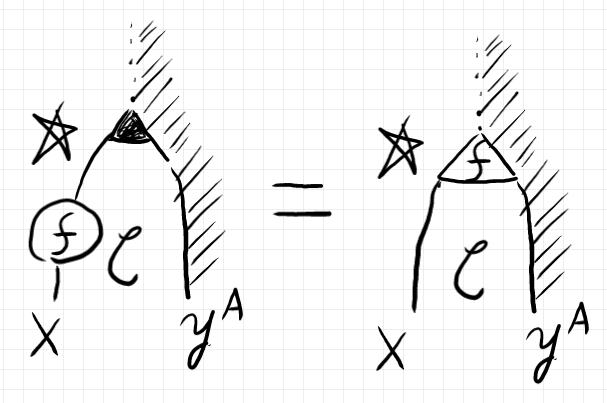
この絵で:
- ワイヤーの方向はどこでも上から下
- '☆' は、単一対象と恒等射だけの自明な圏
- 斜線網掛けは、集合圏 $`{\bf Set}`$
- 点線は、単元集合(集合圏の終対象) $`{\bf 1}`$ のポインティング関手
$`\quad {\bf 1}^\sim : ☆ \to {\bf Set} \In {\bf CAT}`$
- 黒三角は、$`\id_A \in \cat{C}(A, A)`$ のポインティング自然変換(ポインティング関手のあいだの自然変換)
$`\quad {\id_A}^\sim :: {\bf 1}^\sim \Rightarrow \cat{C}(A, A)^\sim : ☆ \to {\bf Set} \In {\bf CAT}`$
- $`f: A \to X \In \cat{C}`$
- $`y^A := \cat{C}(A, \hyp)`$
最近は、「ワイヤーの方向はどこでも上から下」には固執しないで、一部「下から上へのワイヤー」も許して、$`y^A`$(共変関手)の代わりに $`A^y`$(反変関手)を使う設定と描画法を採用してます。
それはともかく、いずれにしても、上の絵図等式の主張していることは:
$`\quad (f^\sim * y^A)(\id_A) = f`$
アスタリスクは関手の図式順結合記号です。
次のように計算で示せます。
$`\quad (f^\sim * y^A)(\id_A)\\
= (f^\sim * \cat{C}(A, \hyp) )(\id_A) \\
= (\cat{C}(A, \hyp)(f))(\id_A) \\
= \cat{C}(A, f)(\id_A) \\
= \cat{C}(\id_A, f)(\id_A) \\
= \id_A; \id_A ; f \\
= f
`$
一般的に(上の $`f`$ とは少し違う設定で)、 $`f:A \to B \In \cat{C}`$ に対して、次の等式が成立します。$`\On`$ は、等式が成立している集合を示します。
- $`\cat{C}(f, B)(\id_B) = f \On \cat{C}(A, B)`$
- $`\cat{C}(A, f)(\id_A) = f \On \cat{C}(A, B)`$
これらの等式は、米田の補題を支えているという意味で“米田の補題の補題”と呼んでいいでしょう。
冒頭で触れた、短く・簡潔な累乗記法を使うと、“米田の補題の補題”は次のように書けます。
- $`B^f (\id_B) = f \On B^A`$
- $`f^A (\id_A) = f \On B^A`$
簡潔すぎて当惑してしまうでしょう。が、慣れればかなり便利です。
外部ホムの記法
外部ホムセットは通常のホムセットです。内部ホム対象は、デカルト閉圏における指数対象です(もっと一般化できますが、とりあえずはコレ)。外部ホムセット、内部ホム対象は次のように書きます。
$`\quad \mrm{Hom}_\cat{C}(\hyp, \hyp) = \cat{C}(\hyp, \hyp) \\
\quad \mrm{hom}_\cat{C}(\hyp, \hyp) = \cat{C}[\hyp, \hyp]
`$
圏 $`\cat{C}`$ が周知なら、下付きの $`\cat{C}`$ は省略し、$`[\hyp,\hyp] = \cat{C}[\hyp, \hyp]`$ と略記します。
累乗記法 $`\hyp^\hyp`$ は、内部ホム対象を表す別記法です。
$`\quad \hyp^\hyp = [\hyp, \hyp] = \mrm{hom}(\hyp, \hyp)`$
無名変数(ハイフン)の場所には圏の対象だけでなくて、射が入ってもかまいません。つまり、外部ホム/内部ホムは関手(二項関手〈双関手〉)になります。
$`\quad \mrm{Hom}_\cat{C} : \cat{C}^\mrm{op}\times \cat{C} \to {\bf Set} \In {\bf CAT}\\
\quad \mrm{hom}_\cat{C} : \cat{C}^\mrm{op}\times \cat{C} \to \cat{C} \In {\bf CAT}
`$
外部ホム関手 $`\mrm{Hom}_\cat{C}`$ の射パートの具体的な定義は次のようになります。セミコロンは、図式順結合記号です。
$`\text{For } f: A \to B, g : C \to D \In \cat{C}\\
\quad \mrm{Hom}_\cat{C}(f, g) : \cat{C}(B, C) \to \cat{C}(A, D) \In {\bf Set}\\
\quad \mrm{Hom}_\cat{C}(f, g) :=\\
\qquad \lambda\, u \in \cat{C}(B, C). f;u;g
`$
集合 $`\cat{C}(B, C)`$ の要素(射)を、$`f, g`$ でサンドイッチ結合するだけです。
集合圏では、外部ホムと内部ホムが一致するので、次のように書けます。
$`\text{For }A, B \in |{\bf Set}|\\
\quad B^A = [A, B] = {\bf Set}(A, B)\\
\text{For } f: A \to B, g : C \to D \In {\bf Set}\\
\quad g^f = [f, g] = {\bf Set}(f, g) = \mrm{Hom}_{\bf Set}(f, g)
`$
一般的には(集合圏以外では)、外部ホムと内部ホムが一致する保証はないし、そもそも内部ホムが存在しないかも知れません。
しかし、$`B^A, g^f`$ という短い・簡潔な記法は魅力的です。そこで、内部ホムの別記法ではなくて、外部ホムの別記法として使ってしまえ、というのが「スピヴァックの指数記法(米田不定元)」の提案です。
この方式では、一般の圏 $`\cat{C}`$ において、次の記法を使います。
$`\text{For }A, B \in |\cat{C}|\\
\quad B^A := \cat{C}(A, B) \;\in |{\bf Set}|\\
\text{For } f: A \to B, g : C \to D \In \cat{C}\\
\quad g^f = \cat{C}(f, g) : \cat{C}(B, C) \to \cat{C}(A, D)\In {\bf Set}\\
\text{For }A, B \in |\cat{C}|\\
\quad y^A := \cat{C}(A, \hyp) : \cat{C} \to {\bf Set} \In {\bf CAT}\\
\quad B^y := \cat{C}(\hyp, B) : \cat{C}^\mrm{op} \to {\bf Set} \In {\bf CAT}
`$
象形文字記法
象形文字記法とは、絵図に似せて文字や記号を選んで、できるだけ容易に絵図をイメージできるようにした記法です。例えば、恒等射、対称〈スワップ〉、対角射〈コピー〉を $`\mrm{I}, \mrm{X}, \Delta`$ で表したり、$`f`$ の右カリー化を $`f^\cap`$ 、その反カリーを $`{f^\cap}_\cup`$ と書く、とかです。
象形文字記法は描画方向に影響されてしまいます。例えば、対角射〈コピー〉を $`\Delta`$ と書くのは、上から下の描画方向を前提しています。下から上なら $`\nabla`$ 、左から右なら $`\triangleleft`$ が適切でしょう。
さて、累乗記法 $`B^A`$ の象形文字記法は、$`A`$ を右肩に置くのをやめて、単純に上に乗せます。
$`\quad \overset{A}{B}\, := \cat{C}(A, B) \;\in |{\bf Set}|`$
ほんとは、優劣がない対等な関係なので字の大きさも同じにしたいのですが、配列・行列にすると場所を取るのでこれで我慢します。
射の累乗記法 $`g^f`$ の代替記法には飾りを付けます。適用(関数への引数渡し)が右引数なら '$`\sqsupset`$' を、左引数なら '$`\sqsubset`$' を飾りに付けます。
$`\text{For } f: A \to B, g : C \to D \In \cat{C}\\
\text{For } u \in \cat{C}(B, C)\\
\quad \overset{f}{g}\sqsupset(u)\, := \cat{C}(f, g)(u) \;\in \cat{C}(A, D)\\
\quad u.\sqsubset\overset{f}{g} := \cat{C}(f, g)(u) \;\in \cat{C}(A, D)
`$
これがなぜ象形文字なのか? は、次の絵図でわかるでしょう。
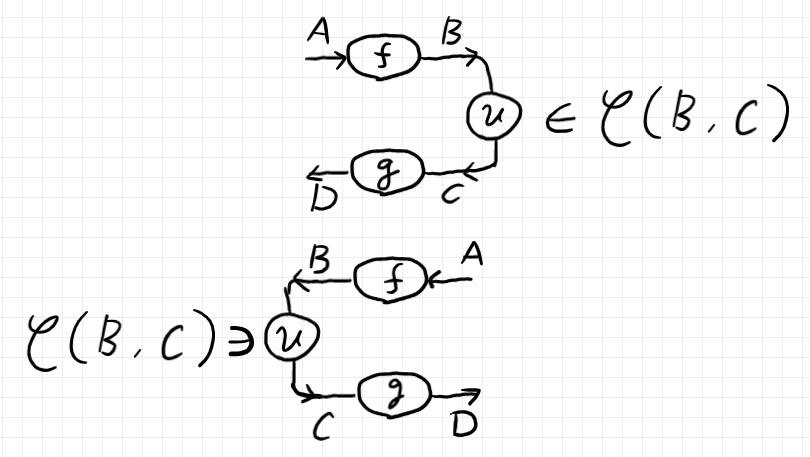
$`\overset{f}{g}\sqsupset`$ と書くか $`\sqsubset\overset{f}{g}`$ と書くかは好みの問題です。
- 引数を右から渡したい、あるいは、$`f`$ (上段)の向きを左から右と考えたいなら $`\overset{f}{g}\sqsupset`$
- 引数を左から渡したい、あるいは、$`g`$ (下段)の向きを左から右と考えたいなら $`\sqsubset\overset{f}{g}`$
どちらを選んだにしろ、しばらくすれば「どっちでもいいや」という気分になるでしょう。そしたら、単に $`\overset{f}{g}`$ でもいいとします。$`\overset{f}{g}`$ のプロファイル(域と余域の仕様)は次のように書けます。
$`\quad \overset{f}{g} = \overset{f}{g}\sqsupset \;: \overset{A}{D} \leftarrow \overset{B}{C} \In {\bf Set}\\
\quad \overset{f}{g} = \,\sqsubset\overset{f}{g} \;: \overset{B}{C} \to \overset{A}{D} \In {\bf Set}
`$
ホムセットのあいだのホム写像(外部ホム関手の射パートの値)は、下段の第二引数の向きで、上段の第一引数とは反対の向きになります。言い方を変えると、上段=第一引数を $`\cat{C}^\mrm{op}`$ の射とみなせば、ホム写像の向きは第一引数($`\cat{C}^\mrm{op}`$ の射)とも同じ向きです。
外部ホムの計算法則
外部ホム=ホム関手 は、反変・共変の二項関手〈双関手〉です。つまり、第一引数に関しては反変関手として振る舞い、第二引数に関しては共変関手として振る舞います。そのことを象形文字記法で書けば次のようになります。
$`\text{For }f:A \to B, f': B \to C \In \cat{C}\\
\text{For }g:D \to E \In \cat{C}\\
\quad \overset{f ; f'}{g} = \overset{f'}{g} ; \overset{f}{g} \;: \overset{C}{D} \to \overset{A}{E} \In {\bf Set}\\
\quad \overset{\id_A ; f}{g} = \overset{f}{g} \;: \overset{B}{D} \to \overset{A}{E} \In {\bf Set}\\
\quad \overset{f ; \id_B}{g} = \overset{f}{g} \;: \overset{B}{D} \to \overset{A}{E} \In {\bf Set}\\
%
\text{For }f:A \to B \In \cat{C}\\
\text{For }g:D \to E, g': E \to F \In \cat{C}\\
\quad \overset{f}{ g; g'} = \overset{f}{g} ; \overset{f}{g'} \;: \overset{B}{D} \to \overset{A}{F} \In {\bf Set}\\
\quad \overset{f}{\id_D; g} = \overset{f}{g} \;: \overset{B}{D} \to \overset{A}{E} \In {\bf Set}\\
\quad \overset{f}{ g ; \id_E} = \overset{f}{g} \;: \overset{B}{D} \to \overset{A}{E} \In {\bf Set}
`$
しばしば、$`\id_A`$ の代わりに単に $`A`$ と書きます。プログラミング言語の言い回しなら、次のようなコアージョン〈coercion | 強制〉規則があります。
- 射が出現すべき文脈で対象が出現したら、それは恒等射とみなす。
例えば、上の恒等射に関する法則をコアージョンを前提に書くと次のようになります。
$`\quad \overset{A ; f}{g} = \overset{f}{g} \;: \overset{B}{D} \to \overset{A}{E} \In {\bf Set}\\
\quad \overset{f ; B}{g} = \overset{f}{g} \;: \overset{B}{D} \to \overset{A}{E} \In {\bf Set}\\
%
\quad \overset{f}{D; g} = \overset{f}{g} \;: \overset{B}{D} \to \overset{A}{E} \In {\bf Set}\\
\quad \overset{f}{ g ; E} = \overset{f}{g} \;: \overset{B}{D} \to \overset{A}{E} \In {\bf Set}
`$
ここに挙げた計算法則(双関手性)は、定義から(あるいは絵を描けば)明らかでしょう。