このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

半グラフの様々な定義

グラフの一種と考えられる組み合わせ構造〈combinatorial structure〉があるのですが、その構造の呼び名が安定してなてく困っています。nLab項目 semi-graph に従い、ここでは「半グラフ〈semi-graph〉」という呼称を採用します。

様々な著者が半グラフを定義して使っているのですが、定義も用語もバラバラで、可視化した図形との関係の説明がまったくないか、あってもミスリーディングだったりします。僕が一番分かりやすいと感じたのは上記nLab項目です。nLab項目のもとになった定義は、ABC予想で有名な望月新一さんによるものです。なお、記事本文中では、望月新一さんを敬称なしの「望月」で参照します。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\parto}{\supseteq\!\to}
\newcommand{\Iff}{\Leftrightarrow }
`$

内容：

参考文献

まず、半グラフに関する参考文献を列挙します。半グラフを主題的に扱っているとは限りませんが、半グラフの定義を含むものです。印象的な部分の画像コピーも貼っておきます。

nLab項目

冒頭に書いたとおり、比較的分かりやすいです。この記事では、nLab項目の定義と説明を基準に考えます。



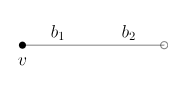
望月

nLab項目から参照されている原典です。



半グラフの定義自体は、次の論文の付録（Appendix: Terminology of Graph Theory）でされています。

ジョイアル／コック

僕が初めて半グラフ（この論文ではファインマン・グラフ〈Feynman graph〉）の定義を見た論文です。唐突で、わけわからんかったです。

  • [JK09-]
  • Title: Feynman graphs, and nerve theorem for compact symmetric multicategories (extended abstract)
  • Authors: André Joyal, Joachim Kock
  • Submitted: 19 Aug 2009
  • Pages: 9p
  • URL: https://arxiv.org/abs/0908.2675



コック

ジョイアル／コック（2009）の発展的内容と言えそうです。このコック論文に有向半グラフ〈directed semi-graph〉（論文内では単に graph）の定義が出てくるので、ファインマン・グラフが無向グラフなのだと察しが付きました。ジョイアル／コック（2009）もコック（2015）も、説明のための絵は一切出てこないです。分かりにくい。

  • [Koc14-15]
  • Title: Graphs, hypergraphs, and properads
  • Author: Joachim Kock
  • Submitted: 14 Jul 2014 (v1), 3 Apr 2015 (v3)
  • Pages: 40p
  • URL: https://arxiv.org/abs/1407.3744
ハックニー

半グラフ（この論文内では単に graph）の定義は、ジョイアル／コックと同じです。しかし、説明のための絵が付いています（後で使います）。有向半グラフやサークル付き半グラフ〈semi-graph with circles〉（後述）も定義しています。



ボリソフ／マニン

ジョイアル／コックより簡略な定義を採用しています。無頂点辺／無頂点ループ（後述）を持たない半グラフだけを扱います。

  • [BM06-11]
  • Title: Generalized operads and their inner cohomomorphisms
  • Authors: D. Borisov, Yu. I. Manin
  • Submitted: 27 Sep 2006 (v1), 7 Jan 2011 (v5)
  • Pages: 71p
  • URL: https://arxiv.org/abs/math/0609748



パターソン

半グラフ（パターソンは半辺グラフ〈half-edge graph〉と呼んでます）と、プログラミング言語Juliaによる半グラフの実装に関する解説です。半グラフの定義はボリソフ／マニンと同じです。半辺〈half edge〉をダート〈dart〉とも呼ぶことは、この解説で知りました。



その他

開放辺〈{open | half | dangling} edge〉を持つグラフ（主に有向グラフ）を、ストリンググラフ〈string graph〉として定義するアプローチは、以下の過去記事で紹介しています。

上記過去記事に幾つかの参考文献を挙げていますが、ひとつだけ引用すると：

  • [KMS12-14]
  • Title: Pattern graph rewrite systems
  • Authors: Aleks Kissinger, Alex Merry, Matvey Soloviev
  • Submitted: 30 Apr 2012 (v1), 1 Apr 2014 (v3)
  • Pages: 13p
  • URL: http://arxiv.org/abs/1204.6695

ディクソン／ダンカン／キッシンジャー〈Lucas Dixon, Ross Duncan, Aleks Kissinger〉達の用語法では、有向半グラフをオープングラフ〈open graph〉と呼びます。

半グラフとは

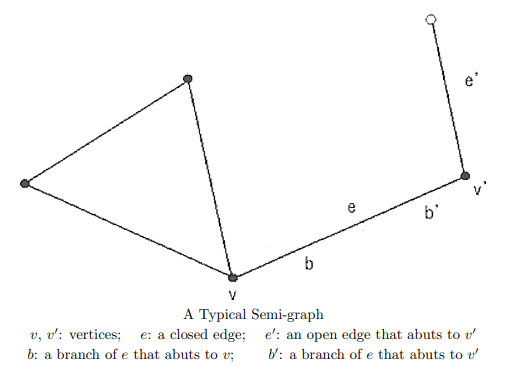
半グラフ〈semi-graph〉とは何であるか？ に対する直感的な説明がなかなかないんですよね。ハックニー論文には絵があるので助かります。

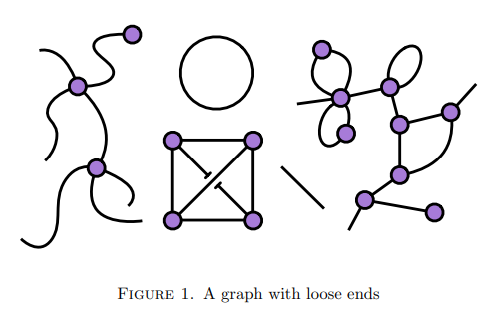
半グラフは、辺〈edge | arc〉が向きを持たない無向グラフ〈undirected graph〉の変種です。通常の無向グラフは、辺の両端に頂点〈vertex | node〉がありますが、半グラフでは頂点を1個しか持たない／全然持たない辺を許します。両端の頂点があるかないかで、辺〈無向辺〉を次のように分類します。

  • 二頂点辺〈two-vertex edge〉 ： 両端ともに頂点を持つ。
  • 単頂点辺〈single-vertex edge〉 ： 片一方だけ頂点を持つ。
  • 無頂点辺〈vertexless edge〉 ： 頂点を持たない。

他に、ループ辺があります。

  • 自己ループ辺〈self-loop edge〉 ： 1つの頂点を持つループ辺。
  • 無頂点ループ〈vertexless loop〉 ： 頂点を持たないループ辺。

ここで、上のハックニーの絵を見て下さい。“$`\boxtimes`$”の形の部分で、辺が切れているように見えますが、これは辺が下を通っていることを示すシルシで、切れているわけではありません。"A graph" とタイトルされているので、全体としてひとつの半グラフですが、5つの連結成分に分けることができます。それぞれの連結成分を、「左連結成分、中央連結成分、右連結成分、円周、線分」と呼びましょう。円周と線分は無頂点ループと無頂点辺であり、ひとつの辺（広義の無向辺）でひとつの連結成分を形成しています。

それぞれの連結成分ごとに、頂点と辺（広義の無向辺）が幾つあるかを勘定してみます。

頂点 二頂点辺 単頂点辺 無頂点辺 自己ループ辺 無頂点ループ
左連結成分 3個 2本 5本 0本 0本 0本
中央連結成分 4個 6本 0本 0本 0本 0本
右連結成分 9個 11本 3本 0本 1本 0本
円周 0個 0本 0本 0本 0本 1本
線分 0個 0本 0本 1本 0本 0本

素朴愚直な定義

前節の絵と説明で、半グラフとは何であるかの直感的イメージはできたと思います。より形式的な定義をしましょう。まずは、前節の辺の分類をそのまま利用して、素朴愚直な定義を構成します。

半グラフの辺（広義の無向辺）の集合を $`E`$ とすると、それは5種類に分類できます。

  1. $`E_2`$ ： 二頂点辺の集合
  2. $`E_1`$ ： 単頂点辺の集合
  3. $`E_0`$ ： 無頂点辺の集合
  4. $`L_1`$ ： 自己ループ辺の集合
  5. $`L_0`$ ： 無頂点ループの集合

これらの集合に空集合があってもかまいません。例えば、通常の無向グラフは、$`E_2, L_1`$ 以外すべて空集合です。

これらの集合は互いに交わらないので、すべての辺（広義の無向辺）の集合 $`E`$ は次のように書けます。（プラス記号は直和の記号ですが、もともと共通部分がないので、タギングで分離する必要はありません。）

$`\quad E = E_2 + E_1 + E_0 + L_1 + L_0`$

辺（広義の無向辺）に接続する頂点の集合を指定すれば、グラフ構造を定義できます。辺に接続する頂点の個数が辺の種類により変わります。また、辺は無向辺なので、接続する頂点を順番付けることはしません。

準備として、“ちょうど$`n`$個の要素からなる部分集合の集合”を定義します。集合 $`X`$ と 自然数 $`n`$ に対して、

$`\quad \mrm{Pow}_n(X) = \{A \in \mrm{Pow}(X) \mid \mrm{card}(A) = n\}`$

ここで、$`\mrm{Pow}(X)`$ は集合 $`X`$ のベキ集合〈powerset〉、$`\mrm{card}(A)`$ は集合 $`A`$ の基数〈cardinality〉（要素の個数）です。

半グラフの頂点の集合を $`V`$ として、次のような写像〈関数〉を考えます。これらは、各種の辺に対し、接続する頂点の集合を対応させます。

$`\quad \varepsilon_2 : E_2 \to \mrm{Pow}_2(V)\\
\quad \varepsilon_1 : E_1 \to \mrm{Pow}_1(V)\\
\quad \varepsilon_0 : E_0 \to \mrm{Pow}_0(V)\\
\quad \lambda_1 : L_1 \to \mrm{Pow}_1(V)\\
\quad \lambda_0 : L_0 \to \mrm{Pow}_0(V)
`$

これらの写像を境界写像〈boundary map〉と呼ぶことにします。辺に、その境界である頂点の集合を対応させるからです。

以上の構成素達をまとめると、

$`\quad (E_2, E_1, E_0, L_1, L_0, V, \varepsilon_2, \varepsilon_1,\varepsilon_0, \lambda_1, \lambda_0)`$

この11項目のタプルがひとつの半グラフを定義します。

この素朴愚直な定義は、論理的に問題があるわけではありませんが、冗長でめんどくさくダサいのは確かです。そこで、もっとスマートな定義を模索することになります。

[注意]
頂点の集合と辺の集合は、通常有限集合だと仮定します。この記事では、特に有限集合の条件は付けていません。半グラフを定義するだけなら、有限性が必須な状況に出会わないからです。
[/注意]

望月の定義： 辺を枝に分割する

nLabの定義＝望月の定義を見ましょう。望月の定義の要点は次のニ項目です。

  1. 無頂点ループは扱わない。
  2. 1本の辺（広義の無向辺）を2本の枝〈branch〉に分割する。

半グラフ（無頂点ループは無い）を $`G`$ として、$`G`$ のすべての辺（広義の無向辺）の集合を $`E`$ とします。辺 $`x\in E`$ を、“真ん中で”（比喩です）チョキンと切って2本に分けます。分割されたそれぞれを、辺 $`x`$ の枝〈branch〉と呼びます。枝という概念が、望月の定義のキモです。

辺 $`x`$ の枝の集合が $`\{x_1, x_2\}`$ のとき、辺と“枝の二元集合”を同一視して、次のように書きます。

$`\quad x = \{x_1, x_2\}`$

したがって、辺とは枝を要素とする二元集合であると言えます。枝に順番はないので「右の枝」とか「根本〈ねもと | source〉の枝」とかは言えませんが、区別できる2本の枝があるのは確実です。

[補足]
辺 $`e\in E`$ と書かずに文字 $`x`$ を使ったのは、すぐ後の具体例で、辺 $`e`$ を具体的な辺の固有名として使うからです。もちろん、名前の種別（束縛変数か自由変数か）とスコープを考慮すれば、同じ名前を使ってもいいのですが、いらぬ混乱を避けるため。
[/補足]

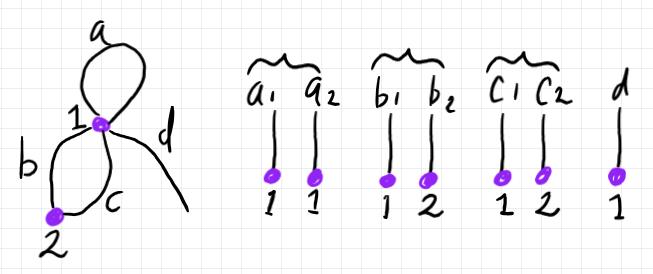
例として、次の単純な半グラフを考えましょう。

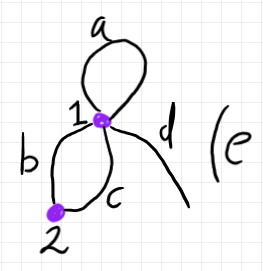
この半グラフの5本の辺 $`a, b, c, d, e`$ を真ん中でチョキンと切ると、10本の枝〈ブランチ〉ができます。すべての枝を描けば次のようです。

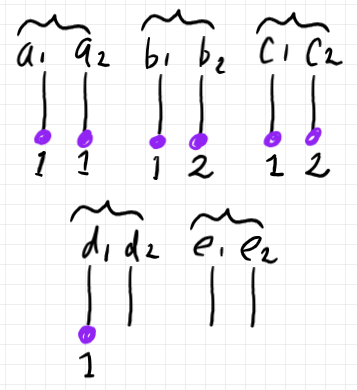
この枝の集合を $`B`$ と書けば、

$`\quad B = \{
a_1, a_2,
b_1, b_2,
c_1, c_2,
d_1, d_2,
e_1, e_2
\}`$

枝のペア〈二元集合〉と辺は同一視していたので、

$`\quad E = \{
\{a_1, a_2\},
\{b_1, b_2\},
\{c_1, c_2\},
\{d_1, d_2\},
\{e_1, e_2\}
\}`$

集合 $`B`$ や $`E`$ だけだと、枝の端にどんな頂点が付いているか／付いてないかわからないので、境界写像（望月のオリジナルの用語では一致写像〈coincidence maps〉）を定義します。境界写像の値は頂点ですが、「頂点が付いてない」ことを表すために $`\bot`$〈ボトム〉を使います。

オリジナルの定義では、各辺 $`x \in E`$ ごとに境界写像〈一致写像〉がひとつずつあります。$`V`$ を頂点の集合として、

$`\quad \zeta_x : x = \{x_1, x_2\} \to V + \{\bot\}`$

例えば、今の例なら：

$`\quad \zeta_a : a = \{a_1, a_2\} \to \{1, 2, \bot\}\\
\qquad \zeta_a(a_1) := 1\\
\qquad \zeta_a(a_2) := 1\\
%
\quad \zeta_b : b = \{b_1, b_2\} \to \{1, 2, \bot\}\\
\qquad \zeta_b(b_1) := 1\\
\qquad \zeta_b(b_2) := 2\\
%
\quad \zeta_c : c = \{c_1, c_2\} \to \{1, 2, \bot\}\\
\qquad \zeta_c(c_1) := 1\\
\qquad \zeta_c(c_2) := 2\\
%
\quad \zeta_d : d = \{d_1, d_2\} \to \{1, 2, \bot\}\\
\qquad \zeta_d(d_1) := 1\\
\qquad \zeta_d(d_2) := \bot\\
%
\quad \zeta_e : e = \{e_1, e_2\} \to \{1, 2, \bot\}\\
\qquad \zeta_e(e_1) := \bot \\
\qquad \zeta_e(e_2) := \bot
`$

境界写像は、すべての枝の集合 $`B`$ で定義されているとしても同じです。

$`\quad \zeta : B \to \{1, 2, \bot\}\\
\qquad \zeta(a_1) := 1\\
\qquad \zeta(a_2) := 1\\
%
\qquad \zeta(b_1) := 1\\
\qquad \zeta(b_2) := 2\\
%
\qquad \zeta(c_1) := 1\\
\qquad \zeta(c_2) := 2\\
%
\qquad \zeta(d_1) := 1\\
\qquad \zeta(d_2) := \bot\\
%
\qquad \zeta(e_1) := \bot \\
\qquad \zeta(e_2) := \bot
`$

境界写像 $`\zeta`$〈ゼータ〉と枝と辺の関係 $`\pi`$〈パイ〉は、次の形で捉えることにします。

$`\require{AMScd}
\begin{CD}
B @>{\zeta}>> V + \{\bot \}\\
@V{\pi}VV @. \\
E {}
\end{CD}\\
\text{ in } {\bf Set}/{\bf FinSet}
`$

ここで$`\pi`$ は、枝に、それを含む辺を対応させる写像です。例えば：

$`\quad \pi(a_1) = a = \{a_1, a_2\}\\
\quad \pi(a_2) = a = \{a_1, a_2\}\\
\quad \pi(b_1) = b = \{b_1, b_2\}\\
\quad \pi(b_2) = b = \{b_1, b_2\}
`$

$`\pi`$ は全射であり、ファイバー（逆像集合）はすべて二元集合で、その二元集合は辺を再現します。

部分写像の表現法

部分写像 $`f:X \parto Y`$ とは、未定義を許す写像〈関数〉です。$`f(x)`$ が未定義のとき、$`f(x) = \bot`$ だとすれば、部分写像 $`f`$ を、$`Y + \{ \bot \}`$ への写像だと思えます。

$`\quad f:X \to Y + \{\bot\}`$

半グラフの定義に使った $`V + \{\bot\}`$ は、部分写像 $`\zeta`$ を表現する方法だったわけです。

部分写像 $`f:X \parto Y`$ があるとき、値が定義されている部分集合を $`A\subseteq X`$ として、

$`\quad f:X \supseteq A \to Y`$

とも書けます。$`X \supseteq A`$ の包含写像（埋め込み写像）を $`\sigma`$ とすると（文字 $`\sigma`$ に特に意味はない）、部分写像は次の形で表現できます。

$`\quad \begin{CD}
X @<{\sigma}<< A @>{f}>> Y
\end{CD}`$

部分写像 $`\zeta: B \to V +\{\bot \}`$ を、上の形に変更しましょう。半グラフの枝の集合 $`B`$ を次の2つの部分にわけます。

  • $`B_1`$ ： 頂点を1つ持つ枝の集合
  • $`B_0`$ ： 頂点を持たない枝の集合

すると、$`B = B_1 + B_0`$ であり、部分写像 $`\zeta`$ は $`B_1`$ 上で定義されていると分かります。よって、次の形に書けます。

$`\require{AMScd}
\begin{CD}
B @<{\sigma}<< B_1 @>{\zeta}>> V\\
@V{\pi}VV @. \\
E {}
\end{CD}\\
\text{ in } {\bf Set}/{\bf FinSet}
`$

半グラフは、この形でも定義できます。$`\pi`$ は今までと同じで、$`\sigma`$ は単射である、という条件は付きます。

パートナー指定対合と同値関係

枝の集合 $`B`$ の要素（つまり枝）には、必ずパートナーがいます。例えば、$`a_1`$ のパートナーは $`a_2`$ であり、$`a_2`$ のパートナーは $`a_1`$ です。枝にそのパートナーを対応させる写像（パートナー指定対合〈partner designation involution〉）を次のように書きます。

$`\quad \iota : B \to B\\
\text{For }x = \{x_1, x_2\}\in E,\; x_1, x_2 \in B\\
\quad \iota(x_1) = x_2\\
\quad \iota(x_2) = x_1
`$

パートナーを指定する写像 $`\iota`$〈イオタ〉は次の性質を持ちます。

  1. $`\iota ; \iota = \iota \circ \iota =\mrm{id}_B`$
  2. $`\forall x \in B.\, \iota(x) \ne x`$

一番目の性質を持つ写像を対合〈involution〉といいます。二番目は、$`\iota`$ が不動点を持たないことです。合わせて、不動点無し対合〈fixpoint-free involution〉です。

$`j:X \to X`$ を対合（不動点はあってもよい）だとして、少し一般論をします。対合 $`j`$ により、集合 $`X`$ 上に同値関係 $`\sim_j`$ を次のように定義できます。

$`\text{For }x, y \in X\\
\quad x \sim_j y :\Iff x = y \lor x = j(y)
`$

$`j`$ が対合であることから、$`\sim_j`$ が同値関係になることはすぐに分かります。また、同値関係 $`\sim_j`$ の同値類は単元集合か二元集合です。

  • $`x`$ が $`j`$ の不動点のとき、$`x`$ の同値類 $`[x]`$ は単元集合 $`\{x\}`$ 。
  • $`x`$ が $`j`$ の不動点でないとき、$`x`$ の同値類 $`[x]`$ はニ元集合 $`\{x, j(x)\}`$ 。

逆に、$`X`$ 上の同値関係が、「同値類が単元集合または二元集合である」とき、$`X`$ 上の対合を定義できます。つまり、次の2つの命題は同値で、対合 $`j`$ と 同値関係 $`\sim`$ が1：1に対応します。

  • 集合 $`X`$ 上に、対合 $`j:X \to X`$ が在る。
  • 集合 $`X`$ 上に、同値類が単元集合または二元集合である同値関係 $`\sim`$ が在る。

対合 $`j`$ に不動点がないと、対応する同値関係 $`\sim`$ の同値類はすべて二元集合になります。つまり、次の2つの命題は同値です。

  • 集合 $`X`$ 上に、不動点無し対合 $`j:X \to X`$ が在る。
  • 集合 $`X`$ 上に、同値類が二元集合である同値関係 $`\sim`$ が在る。

半グラフの枝の集合 $`B`$ に戻ると、次はすべて同値です。全射 $`\pi`$ 、同値関係 $`\sim`$ 、不動点無し対合 $`\iota`$ の三者が相互に移りあえるのです。

  • ファイバー〈逆像集合〉がすべて二元集合である全射 $`\pi: B \to E`$ が在る。
  • 集合 $`B`$ 上に、同値類がすべて二元集合である同値関係 $`\sim`$ があり、商集合 $`B/\!\sim`$ が $`E`$ と同型である。
  • 集合 $`B`$ 上に、不動点無し対合 $`\iota :B \to B`$ が在り、対応する同値関係が $`\sim`$ である。

以上の状況をまとめると、次のような図式になります。

$`\xymatrix{
% @(inDir, outDir)
B \ar@(ul, dl)[0,0]_{\iota}
\ar[d]_{\pi}
\\
E
}\\
\text{where } E \cong B/\!\sim`$

ジョイアル／コックの定義： 埋め込みと不動点無し対合

望月の定義による半グラフを $`G`$ とすると、$`G = (E, B, V, \zeta, \pi)`$ （下の図）と書けます。

$`\begin{CD}
B @>{\zeta}>> V + \{\bot \}\\
@V{\pi}VV @. \\
E {}
\end{CD}\\
\text{ in } {\bf Set}/{\bf FinSet}
`$

次の条件があります。

  • $`\pi`$ は、すべてのファイバー〈逆像集合〉が二元集合である全射である。

部分写像である境界写像 $`\zeta`$ を、埋め込み $`\sigma`$ と通常の写像としての $`\zeta`$ を使って表現すると：

$`\begin{CD}
B @<{\sigma}<< B_1 @>{\zeta}>> V\\
@V{\pi}VV @. \\
E {}
\end{CD}\\
\text{ in } {\bf Set}/{\bf FinSet}
`$

$`B`$ 上の不動点無し対合 $`\iota`$ も書き込むと：

$`\xymatrix{
% @(inDir, outDir)
B \ar@(ul, dl)[0,0]_{\iota}
\ar[d]_{\pi}
& B_1 \ar[l]_{\sigma} \ar[r]^{\zeta}
& V
\\
E
}\\
\text{ in } {\bf Set}/{\bf FinSet}
`$

$`B`$ 上に不動点無し対合 $`\iota`$ があれば、$`E`$ は $`B/\!\sim_\iota`$ として再現できるので省略しましょう。

$`\xymatrix{
% @(inDir, outDir)
B \ar@(ul, dl)[0,0]_{\iota}
& B_1 \ar[l]_{\sigma} \ar[r]^{\zeta}
& V
}\\
\text{ in } {\bf Set}/{\bf FinSet}
`$

これが、ジョイアル／コックの半グラフ〈ファインマン・グラフ〉の定義です。つまり、ジョイアル／コック・スタイルの半グラフは $`G = (B, B_1, V, \iota, \sigma, \zeta)`$ であり、次の条件を満たすものです。

  • $`\iota : B \to B`$ は不動点無し対合である。
  • $`\sigma : B_1 \to B`$ は単射である。

ボリソフ／マニンの定義： 無頂点辺が不要な場合

ボリソフ／マニンの半グラフの定義では、無頂点辺は扱えません。その代わり定義が単純になります。

枝の集合 $`B`$ 上の対合 $`\iota: B \to B`$ は考えますが、不動点無しの条件は外します。すると、枝は次のどちらかになります。

  1. $`\iota(x) \ne x`$ である枝 $`x\in B`$
  2. $`\iota(x) = x`$ である枝 $`x\in B`$

一番目の種類の枝は、カップル $`x, \iota(x)`$ で一本の二頂点辺を表し、ニ番目の種類の枝は、単独で一本の単頂点辺を表すと約束します。

この約束のもとでは、$`G = (B, V, \iota, \zeta)`$ が、無頂点ループと無頂点辺を持たない半グラフを表現します。

$`\xymatrix{
% @(inDir, outDir)
B \ar@(ul, dl)[0,0]_{\iota}
\ar[r]^{\zeta}
& V
}\\
\text{ in } {\bf Set}/{\bf FinSet}
`$

次の条件は要請します。

  • $`\iota : B \to B`$ は対合である。

先の具体例から無頂点辺を取り除いた半グラフをボリソフ／マニンの定義で表すなら次のようになります。枝としての $`d`$ が対合 $`\iota`$ の不動点になり、単頂点辺を表します。

半グラフの各部の呼び名

半グラフ構造の呼び名は以下の表のようです。

望月 半グラフ〈semi-graph〉
ジョイアル／コック ファインマン・グラフ〈Feynman graph〉
ボリソフ／マニン グラフ〈graph〉
ハックニー グラフ〈graph〉
パターソン 半辺グラフ〈half-edge graph〉

単頂点辺や枝に対する呼び名は色々です。しかも、単頂点辺なのか枝なのか、二頂点辺以外の辺なのか、何を指しているのか判然としないこともあります。呼び名だけ列挙しておくと：

  1. 半辺〈half edge〉
  2. 開放辺〈{open | dangling} edge〉
  3. 枝〈branch〉
  4. フラグ〈flag〉
  5. ダート〈dart〉

呼び名は錯綜しているだけでなく、ミスリーディングなこともあります。呼び名がどうであれ、半グラフという概念は既に説明したような組み合わせ構造のことですから、呼び名に拘らないのが吉です。

おわりに

望月の半グラフと、ジョイアル／コックのファインマン・グラフは、定義の方法が違うだけで同じ概念です。ボリソフ／マニンのグラフは、ジョイアル／コック方式の簡略化で無頂点辺の記述は諦めます。ハックニーはジョイアル／コックの定義を採用しており、パターソンはボリソフ／マニンの定義を採用しています。

いずれの定義でも、無頂点ループは扱えません。無頂点ループはサークル〈circle〉とも呼ばれ、テンパリー／リーブ圏（例えば「テンパリー／リーブ圏とカウフマンのスケイン関係式」参照）の計算などではサークルが出現します。サークルを持つ半グラフ（サークル付き半グラフ〈semi-graph with circles〉）の扱い方は、ハックニー論文の付録Cにあります（ハックニーはサークルを nodeless loop と呼んでいます）。

この記事で述べた半グラフは辺に向きがありませんが、有向半グラフ〈directed semi-graph〉については、コックの論文とハックニーの論文に書いてあります。有向半グラフは、圏・複圏・多圏のストリング図の基礎として重要です。