亜群をベースとする圏類似構造：コステロの事例 - 檜山正幸のキマイラ飼育記 (はてなBlog)

ケビン・コステロが定義した“グラフの圏”は、実際には圏になってません。しかし、ほとんど圏と同様に扱えますし、役に立ちます。射の結合可能性条件を等式から同型に緩めた事例として興味深く示唆に富みます。$`\newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\In}{\text{ in } }`$

内容：

コステロの“グラフの圏”
半グラフ
- ツリー、林、根なし／根付き
有限バンドルの亜群
亜群上の圏類似構造

コステロの“グラフの圏”

コステロは以下の論文のなかで $`{\bf Graphs}`$ という“圏”を定義しています。

[Cos04-04]
Title: The A-infinity operad and the moduli space of curves
Author: Kevin Costello
Submitted: 2 Feb 2004 (v1), 15 Sep 2004 (v2)
Pages: 14p
URL: https://arxiv.org/abs/math/0402015

$`{\bf Graphs}`$ は奇妙な“圏”です。対象がグラフなのではなくて、射がグラフです。グラフは通常の有向グラフではなくて、無向半グラフ（「半グラフの様々な定義」参照）です。そればかりではなくて、射（実体は半グラフ）の結合可能性〈composability〉の定義も通常の圏とは違います。また、射の結合は一意的には決まりません。

コステロは何の断りもなくこの奇妙な構造を「圏」と呼んでいます。「ほぼ圏だ」とは言えますが、どう考えても通常の圏にはなっていません。こういった圏によく似た奇妙な構造をちゃんと考えてみるのは意味がありそうです。と言うのも、比較的最近、コステロの“圏”とは別な“圏もどき”に出会っているので、“圏もどき”はけっこう出現するみたいだからです。

「亜群上の豊穣複グラフ：豊穣化・基礎強化の例」より：

最近、豊穣圏と内部圏が混ざったような“圏もどき”に出会いました。ソレを扱うには豊穣化だけでは不十分で、内部化とはズレているので内部化でも片付きません。

今回の話題とは少し違う状況ですが、圏によく似ているが圏ではない例を以下の過去記事で扱っています。

いずれの場合も、等式的条件や等式的法則における等式を、亜群の射（定義より可逆）で置き換えています。亜群ベースの構造が、意外と遍在している（実は奇妙ではない）のかも知れません。

半グラフ

コステロの $`{\bf Graphs}`$ の基本となるのは半グラフ（コステロは単に「グラフ」と呼んでいます）です。過去記事「半グラフの様々な定義」において、半グラフ〈semi-graph〉の定義を幾つか挙げました。コステロの定義はボリソフ／マニンの定義（「半グラフの様々な定義」参照）と同じです。ボリソフ／マニンの繰り返しになりますが、半グラフは次の構成素からなります。

有限集合 $`V`$ ：頂点〈vertex〉達の集合
有限集合 $`H`$ ：半辺〈half-edge〉達の集合
写像 $`\pi : H \to V`$ ：半辺に端点〈境界点〉を対応させる。（望月の用語では一致写像〈coincidence map〉）
対合写像 $`\sigma:H \to H`$ ：半辺にそのパートナーを対応させる。

コステロは、半辺を辺の芽〈germm | ジャーム〉とも呼んでいます。この定義（ボリソフ／マニン流）の特徴は：

写像 $`\pi`$ は全域写像なので、端点がない半辺は許されない。
そのため、無頂点辺、無頂点ループは表現できない。
対合写像 $`\sigma`$ は不動点を持ってもよい。

半辺の幾何的実現は片一方が開いた区間 $`\{x\in {\bf R}\mid 0\le x\lt 1\}`$ です。$`\sigma`$ によるパートナーとくっ付くと、両端の境界点を含む閉区間の形状になりますが、パートナーがいない（正確には自分自身がパートナーである）半辺もあります。このような状況を表すために次の定義をします。

$`T := \mathrm{Fixpoint}(\sigma) \subseteq H`$ ： $`\sigma`$ の不動点をテール〈tail | 尾〉と呼ぶ。
$`E := H/\sim_\sigma`$ ： $`\sim_\sigma`$ は、$`\sigma`$ で互いに移れるという同値関係。同値類を辺と呼ぶ。

テールの集合 $`T`$ は、厳密に言えば $`E`$ の部分集合ではありませんが、商集合への標準射影を経由して $`T \subseteq E`$ と考えます。区別したいときは、$`E`$ の要素とみたテールは外部辺〈external edge〉と呼びます。ファインマン図〈Feynman diagram〉でいえば外線〈external line〉に相当します。

ここから先は、半グラフに関連する概念で、過去記事「半グラフの様々な定義」にはなかったものを定義します。この記事では使わない概念も“ついでに”書いています。

ツリー、林、根なし／根付き

半グラフ $`\gamma`$ の幾何的実現〈geometric realization〉は、目で見える1次元的図形になります。この図形が連結〈connected〉なとき、半グラフも連結〈connected〉だ、といいます。可縮〈contractible〉も幾何的概念・用語をそのまま使います。

連結かつ可縮な半グラフをツリー〈木〉といいます。今定義したツリーは根〈ルート〉は指定されていません。ツリーのテール（それが在るとして）を1つ指定したツリーが根付きツリー〈rooted tree〉です。コステロの定義では、根〈ルート〉は頂点ではなくてテールです。したがって、ひとつの頂点だけの半グラフはツリーですが、根付きツリーにはなれません。テールと外部辺を同一視するなら、ルートは外部辺だ、とも言えます。

半グラフ $`\gamma`$ に対して、その連結成分の集合〈set of connected components〉を $`C = C(\gamma)`$ と書きます。ここでも幾何的概念・用語を流用しています。$`C`$ の要素は $`\gamma`$ の部分半グラフと考えます。

半グラフ $`\gamma`$ の連結成分（部分半グラフと考えた $`C = C(\gamma)`$ の要素）がすべてツリーのとき、$`\gamma`$ を林〈forest〉と呼びます。林のすべての連結成分（定義よりツリー）にルートが指定されているときは根付き林〈rooted forest〉と呼びます

コステロは定義してないのですが、頂点をひとつだけ持つツリーをカローラ〈corolla〉とか低木〈shrub〉と呼びます。低木は、ひとつの頂点と幾つか（0かも知れない）のテールからなります。ルート〈根〉としてひとつのテールが指定された低木を根付き低木〈rooted shrub〉と呼びます。低木林〈shrub forest〉と根付き低木林〈rooted shrub forest〉の定義は明らかでしょう。

有限バンドルの亜群

$`{\bf FinSet}`$ を有限集合と写像の圏とします。$`I, J\in |{\bf FinSet}|`$ のとき、写像 $`p:I \to J \In {\bf FinSet}`$ を有限バンドル〈finite bundle〉と呼びます。単なる写像をバンドルと呼ぶココロは、逆像 $`p^{-1}(j)`$ をファイバーとみなして、ファイバーを束ねて $`I`$ ができ上がっているからです。幾何に出てくるバンドルとは違って、写像 $`p`$ に何の条件も付けません。ファイバーが空になることもあります。

有限バンドルを対象として、そのあいだの同型射を射とする亜群を $`{\bf FBG}`$ （finite bundle groupoid | groupoid of finite bundles）とします。この亜群の射は、次の図式を可換にする同型写像 $`f_0, f_1`$ のペアです。

$`\require{AMScd}
\quad \begin{CD}
I @>{f_1}>> I'\\
@V{p}VV @VV{p'}V \\
J @>{f_0}>> J'
\end{CD}\\
\quad \text{commutative in }{\bf FinSet}
`$

次のように書きます。

$`\quad f = (f_0, f_1) : [p:I \to J] \to [p':I' \to J'] \In {\bf FBG}`$

コステロは、$`[I \twoheadrightarrow J]`$ という変わった矢印記号を使っていますが、ここでは、ブラケットで囲むだけで普通の矢印記号を使います。

$`{\bf FBG}`$ の対象を一文字 $`A`$ などで書いたときは、$`A = [p_A :A_1 \to A_0]`$ とします。この書き方だと：

$`\quad f = (f_0, f_1) : [p_A:A_1 \to A_0] \to [p_B: B_1 \to B_0] \In {\bf FBG}`$

$`{\bf FBG}`$ の射は（定義より）すべて可逆であることに注意してください。

$`\quad f^{-1} = (f_0^{-1}, f_1^{-1}) : [p_B: B_1 \to B_0] \to [p_A: A_1 \to A_0] \In {\bf FBG}`$

亜群上の圏類似構造

半グラフ（コステロのグラフ）を $`\alpha, \beta`$ などで書くことにします。半グラフ $`\alpha`$ の構成素と半グラフから容易に構成できる集合・写像は次のように書きます。

$`V(\alpha)`$ ： $`\alpha`$ の頂点の集合
$`H(\alpha)`$ ： $`\alpha`$ の半辺の集合
$`\pi_\alpha: H(\alpha) \to V(\alpha)`$ ： $`\alpha`$ の半辺の境界写像
$`\sigma_\alpha : H(\alpha) \to H(\alpha)`$ ： $`\alpha`$ の半辺のパートナー指定対合
$`T(\alpha)`$ ： $`\alpha`$ のテール（外部辺と一対一対応）の集合
$`E(\alpha)`$ ： $`\alpha`$ の辺の集合
$`C(\alpha)`$ ： $`\alpha`$ の連結成分の集合
$`\rho_\alpha : T(\alpha) \to C(\alpha)`$ ： $`\alpha`$ のテールに所属する連結成分を対応させる写像

$`t\in T(\alpha)`$ は外部辺と同一視できます。どんな辺も（頂点も）、ひとつの連結成分に含まれます。外部辺とみなした $`t`$ が所属する連結成分が $`\rho_\alpha(t) \in C(\alpha)`$ です。

さて、コステロの“グラフの圏” $`{\bf Graphs}`$ を定義しましょう。$`{\bf Graphs}`$ があたかも圏であるかのようにみなして、用語・記法を使います。

“グラフの圏”の射の集合 $`\mrm{Mor}({\bf Graphs})`$ は、すべての半グラフからなる（大きい）集合です。対象の集合は、$`|{\bf FBG}|`$ です。つまり、有限バンドルが対象となります。射（半グラフ）の域・余域は次のように定義します。

$`\quad \mrm{dom}(\alpha) : = [\pi_\alpha : H(\alpha) \to V(\alpha)] \in |{\bf FBG}|\\
\quad \mrm{cod}(\alpha) : = [\rho_\alpha : T(\alpha) \to C(\alpha)] \in |{\bf FBG}|
`$

$`{\bf Graphs}`$ の対象（$`{\bf FBG}`$ の対象） $`A:[p_A : A_1 \to A_0]`$ に対する恒等射は例えば次のような半グラフになります。ちゃんと書き下すのは面倒なので絵で察してください。

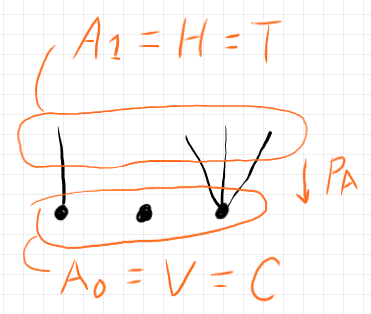
通常の意味で2つの射 $`\alpha`$ と $`\beta`$ が結合可能であるとは、$`\mrm{cod}(\alpha) = \mrm{dom}(\beta)`$ のときです。これは次を意味します。

$`\quad \begin{CD}
T(\alpha) @>{\rho_\alpha}>> C(\alpha)\\
@| @| \\
H(\beta) @>{\pi_\beta}>> V(\beta)
\end{CD}\\
\quad \text{commutative in }{\bf FinSet}
`$

この場合 $`\gamma = \alpha ; \beta`$ は定義できます。幾何的イメージに頼って大雑把に言うと； $`\beta`$ の頂点を、対応する（実は等しい）$`\alpha`$ の連結部分半グラフで置き換えて得られた半グラフが $`\gamma`$ です。この結合は、「回路代数とグラフ置換モナド」のグラフ置換操作と事実上同じものです。

$`{\bf Graphs}`$ における結合は、必ずしも $`\mrm{cod}(\alpha) = \mrm{dom}(\beta)`$ でなくても定義できます。結合可能性の条件は等式ではなくて、次の同型性です。

$`\quad \mrm{cod}(\alpha) \cong \mrm{dom}(\beta) \In {\bf FBG}`$

もっと詳しく言えば：

$`\quad \exists f.\, f : \mrm{cod}(\alpha) \to \mrm{dom}(\beta) \In {\bf FBG}`$

このような $`f`$ が存在すれば、自動的に逆 $`f^{-1}`$ は存在します（$`{\bf FBG}`$ は亜群だから）。

結合可能性を表す図式は次のようになります。

$`\quad \begin{CD}
T(\alpha) @>{\rho_\alpha}>> C(\alpha)\\
@V{f_1}VV @VV{f_0}V \\
H(\beta) @>{\pi_\beta}>> V(\beta)
\end{CD}\\
\quad \text{commutative in }{\bf FinSet}
`$

亜群 $`{\bf FBG}`$ の射 $`f = (f_0, f_1)`$ で対応を取って、$`\beta`$ の頂点を、$`\alpha`$ の連結部分半グラフで置き換えることができます。

このようにして定義した結合の結果は、亜群の射 $`f`$ に依存するので、$`\alpha, \beta`$ から一意的には決まりません。しかし、up-to-iso では決まります。

従来は等式で成立していた条件・法則が、亜群の射による up-to-iso にゆるくなる、という現象は次の過去記事でも述べています。

亜群による等式のリラクゼーション〈緩化〉は考慮に値する現象のようです。