「半グラフの様々な定義」に対する補遺です。
望月/ジョイアル/コック方式の半グラフの定義では、サークル〈無頂点ループ〉を表すことはできません。ボリソフ/マニン方式ではさらに、無頂点辺も表現できません。
枝〈ブランチ〉の集合上に、不動点のない対合を考えるジョイアル/コック方式と、不動点があってもいいとするボリソフ/マニン方式のアイディアを組み合わせると、サークル〈無頂点ループ〉を持つ半グラフも表現できます。その方法が良いかどうかは疑問だけど(最後の段落参照)。
次の例を考えます。
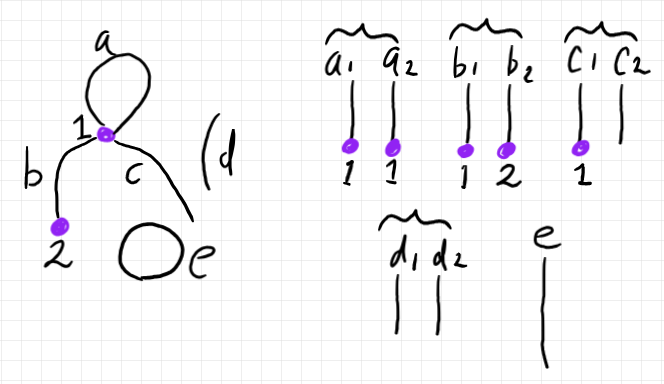
図の左側はサークルを持つ半グラフで、5本の辺〈広義の無向辺〉を持ちます。それぞれの辺の種類は次のようになります。
| 名前 | 種類 |
|---|---|
| a | 自己ループ辺 |
| b | 二頂点辺 |
| c | 単頂点辺 |
| d | 無頂点辺 |
| e | サークル〈無頂点ループ〉 |
それぞれの辺を、“真ん中で”チョキンと切ると、9本の枝ができます(上図の右側)。10本にならないのは、サークル $`e`$ を切っても2本の枝に分解されないからです。枝の集合 $`B`$ 上でパートナー指定写像(「半グラフの様々な定義」参照)$`\iota`$ を考えます。枝としての $`e`$ のパートナーは自分なので、$`e \in B`$ は対合 $`\iota`$ の不動点になります。
$`B'`$ はパートナーを持つ枝の集合とします。$`B' \subseteq B`$ であり、$`B'`$ 上に制限した対合 $`\iota'`$ は不動点を持ちません。頂点を持つ枝の集合を $`{B'}_1`$ とします。$`{B'}_1`$ の要素にその頂点を対応させる写像〈境界写像〉を $`\zeta : {B'}_1 \to V`$ とします。
これらの構成素をまとめると、次の図になります。
$`\xymatrix{
% @(inDir, outDir)
B \ar@(dr, dl)[0,0]^{\iota}
& B' \ar@(dr, dl)[0,0]^{\iota'} \ar[l]^{\sigma'}
& {{B'}_1} \ar[l]^{\sigma} \ar[r]^{\zeta}
& V
}`$
この図で表現される構造は、一般的な「サークルを持つかも知れない半グラフ」を表現可能です。ただし、次の条件は仮定します。
- $`\sigma`$ は単射である。
- $`\iota'`$ は不動点無し対合〈fixpoint-free involution〉である。
- $`\sigma'`$ は単射である。
- $`\iota`$ は対合である。
- $`x \in (B\setminus \sigma(B'))`$ は、$`\iota`$ の不動点である。
- 以下の図式が可換になる。
$`\require{AMScd}
\begin{CD}
B @<{\sigma'}<< B' \\
@V{\iota}VV @VV{\iota'}V\\
B @<{\sigma'}<< B'
\end{CD}\\
\text{commutative in }{\bf Set}/{\bf FinSet}
`$
けっこう面倒。望月/ジョイアル/コックの意味のサークル無し半グラフ $`G`$ に、サークルの集合 $`C`$ を指定したペア $`(G, C)`$ でも同じことですね。もっと安直な定義として、サークル無し半グラフ $`G`$ とサークル(有限個と仮定)が幾つ在るか勘定した自然数 $`n`$ のペア $`(G, n)`$ でサークル付き半グラフを表すこともできます。用途によっては、$`(G, n)`$ でもこと足りるかも知れません。
[追記]
有限半グラフを幾何的・位相的に考えることもできます。
$`J`$ は $`\{x\in {\bf R} \mid 0 \lt x \lt 1\}`$ という開区間とします。$`S^1`$ は円周です。位相空間 $`X`$ とその部分集合 $`V`$ の組 $`(X, V)`$ が次の条件を満たすとき、有限半グラフです。
- $`V`$ は有限集合である。k個の要素を持つとする。
- $`V`$ を取り除いた位相空間 $`X\setminus V`$ は、n個の $`J`$ とm個の $`S^1`$ の直和に同相である。
kが頂点の個数、nが辺の本数、mがサークルの個数になります。
[/追記]