強化ファインマン・グラフとバタニン／バーガー半グラフ - 檜山正幸のキマイラ飼育記 (はてなBlog)

「幾何半グラフの組み合わせ的表現（新方式）」で提案した組み合わせ半グラフを、ジョイアル／コック半グラフと比較してみます。新しい方式は、ジョイアル／コック方式より表現力が高くなっています。また、バタニン／バーガー半グラフを紹介し、新しい方式とバタニン／バーガー方式も比較してみます。新しい方式とバタニン／バーガー方式は同等な表現力を持ちます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\In}{\text{ in } }
\newcommand{\bdry}{\partial }
\newcommand{\Imp}{\Rightarrow }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{－} }
\newcommand{\base}[1]{ {{#1}\!\lrcorner} }
`$

半グラフの定義については、以下の過去記事を参照してください。

半グラフの様々な定義

内容：

ジョイアル／コックの半グラフ〈ファインマン・グラフ〉
強化ファインマン・グラフ
バタニン／バーガーの半グラフ

ジョイアル／コックの半グラフ〈ファインマン・グラフ〉

ジョイアル／コックの半グラフは、ファインマン・グラフ〈Feynman graph〉と呼ばれ、次の論文で定義されました。

[JK09-]
Title: Feynman graphs, and nerve theorem for compact symmetric multicategories (extended abstract)
Authors: André Joyal, Joachim Kock
Submitted: 19 Aug 2009
Pages: 9p
URL: https://arxiv.org/abs/0908.2675

ファインマン・グラフを定義する図式は以下のとおりです（画像コピー）。

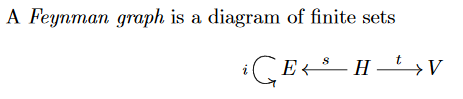
オリジナルの用語・記法はミスリーディングです。

$`E`$ ：辺〈edge〉の集合
$`H`$ ：半辺〈half-edge〉の集合
$`s`$ ：ソース写像
$`t`$ ：ターゲット写像
$`i`$ ：不動点なし対合

対合以外はまったく不適切な呼称です。$`E`$ の要素は辺ではなくて半辺〈フラグ〉です。$`H`$ の要素が境界点〈端点〉を持つのに対して、$`E`$ には境界点を持たない半辺も含まれます。ソース写像 $`s`$ とは、単なる埋め込みです。$`H \subseteq E`$ とみなすと、$`E\setminus H`$ が境界点を持たない半辺（辺じゃありません）です。

ターゲット写像 $`t`$ は、ソース写像 $`s`$（単なる埋め込み）との双対性や対称性は何もなくて、半辺に境界点を対応させる境界写像〈boundary map〉です。対合 $`i`$ で対応する2つの半辺〈フラグ〉のペア〈カップル〉が1つの辺を定義します。辺の集合は $`E`$ じゃなくて、$`E/\!\sim_i`$ です。$`\sim_i`$ は不動点なし対合が誘導する同値関係です。

というわけなので、次のようにリネームします。

$`\quad \xymatrix{
% @(inDir, outDir)
F \ar@(ul, dl)[0,0]_{\iota}
& F' \ar[l]_{j} \ar[r]^-{\bdry}
& V
}\\
\quad \iota; \iota = \mrm{id}_F \text{ (fixed-point free)}
`$

$`F`$ ：フラグ〈flag〉の集合
$`F'`$ ：境界点を持つフラグの集合
$`j`$ ：埋め込み写像
$`\bdry`$ ：境界写像
$`\iota`$ ：不動点なし対合

スパン $`F \leftarrow F' \to V`$ は左脚が単射のスパンなので、部分写像を定義していることになります。部分写像の表現として、未定義値〈ボトム〉 $`\bot`$ を使うと次の形になります。$`F'`$ は不要になります。

$`\quad \xymatrix{
% @(inDir, outDir)
F \ar@(ul, dl)[0,0]_{\iota} \ar[r]^-{\bdry}
& V + \{\bot\}
}\\
\quad \iota; \iota = \mrm{id}_F \text{ (fixed-point free)}
`$

以下、ファインマン・グラフ〈ジョイアル／コック半グラフ〉はこの形で考えます。

なお、ファインマン・グラフに関しては、以下の論文の第3章 Graphs and their morphisms が詳しいです。

[Ray19-22]
Title: Graphical combinatorics and a distributive law for modular operads
Author: Sophie Raynor
Submitted: 14 Nov 2019 (v1), 11 Oct 2022 (v3)
Pages: 66p
URL: https://arxiv.org/abs/1911.05914

強化ファインマン・グラフ

「幾何半グラフの組み合わせ的表現（新方式）」で提案した組み合わせ半グラフを強化ファインマン・グラフ〈enhanced Feynman graph〉と呼ぶことにします。ジョイアル／コックのファインマン・グラフは、強化ファインマン・グラフの特別なものになります。

強化ファインマン・グラフは、次の図式で定義されます。

$`\quad \xymatrix{
% @(inDir, outDir)
F \ar@(ul, dl)[0,0]_{\iota} \ar[r]^-{\bdry}
& V + W + \{\infty\}
}\\
\quad \iota; \iota = \mrm{id}_F \text{ (fixed-point free)}
`$

ファインマン・グラフは、$`W = \emptyset`$ である強化ファインマン・グラフです。特殊な要素の記号が $`\bot`$ か $`\infty`$ かはどうでもいいことです。

強化ファインマン・グラフで“強化”された点は、例外ループ〈無頂点ループ〉を表現できることです。$`W`$ の要素はダミー頂点〈dummy vertex〉で、例外ループと一対一に対応します*1。そのことは次の条件で規定されます。

$`\text{For }f\in F\\
\quad \bdry(f)\in W \Imp \bdry(\iota(f)) = \bdry(f)\\
\text{For }w\in W\\
\quad \mrm{card}(\bdry^{-1}(w)) = 2
`$

以下の図は、例外ループと例外辺を持つ半グラフを強化ファインマン・グラフとみなしたものです（詳細は「幾何半グラフの組み合わせ的表現（新方式）」参照）。レンガ色のバッテンはダミー頂点です。レンガ色の短い線は辺をフラグに切り分ける切断線、頂点を持たないフラグに $`\infty`$ をマークしています。

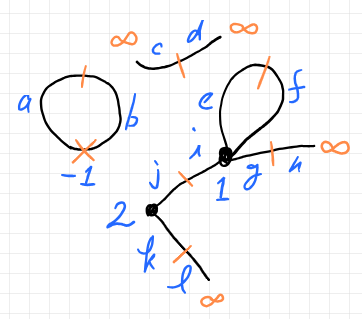
強化ファインマン・グラフの辺〈edge〉は、$`F/\!\sim_\iota`$ の要素です。同値類は、$`\iota`$ でペアリングされた二元部分集合〈カップル〉になります。辺は以下の4パターンのいずれかになります。

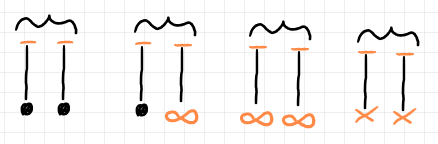
左から、内部辺〈internal edge〉、外部辺〈external edge | 開放辺 | open edge〉、例外辺〈exceptional edge〉、例外ループ〈exceptional loop〉です。例外辺は特殊な外部辺、例外ループは特殊な内部辺とみなします。

ちなみに、ボリソフ／マニン半グラフを強化ファインマン・グラフに変換するには、一点コンパクト化（「半グラフに関わる諸概念 // 半グラフの一点コンパクト化と一点削除」参照）すればOKです。強化ファインマン・グラフは、ジョイアル／コック半グラフとボリソフ／マニン半グラフの一般化になっています。

バタニン／バーガーの半グラフ

バタニン／バーガーの半グラフは、次の論文の Part 4. Graphs, trees and graph insertion で定義されています。

[BB13-17]
Title: Homotopy theory for algebras over polynomial monads
Authors: Michael Batanin, Clemens Berger
Submitted: 1 May 2013 (v1), 6 Feb 2017 (v7)
Pages: 95p
URL: https://arxiv.org/abs/1305.0086

[BB13-17] Part 4 には、他の半グラフの解説もあって便利です。ジョイアル／コック半グラフ以外に、ゲッツラー／カプラノフ〈Getzler-Kapranov〉、ジョンソン／ヤウ〈Johnson-Yau〉、ジョイアル／ストリート〈Joyal-Street〉の半グラフが解説されています。

バタニン／バーガーの定義はちょっと変わっていて、半グラフを有限圏（対象も射も有限個である圏）として定義します。半グラフの接続関係〈incidence relation〉を圏にエンコードして何が嬉しいのか？イマイチわからないのですが、自動的に2-圏が得られたりはします。

形式的な定義をいきなり見てもわかりにくいので、バタニン／バーガーのアイディアを説明します。フラグにより辺を表現するのは他の定義と同じですが、フラグ一本だけで辺を表現するのと、同じフラグを“ニ回使って”辺を表現するケースがあります。

2本の頂点付きフラグのペアは、内部辺を表現する。
1本の頂点付きフラグだけで、外部辺〈開放辺〉を表現する。
1本の無頂点フラグだけで、例外辺を表現する。
1本の無頂点フラグを“二回使って”、例外ループを表現する。

「表現する」とは、フラグ、頂点、辺を表す対象のあいだを射で結ぶことです。強化ファインマン・グラフの辺とのあいだには以下のような対応があります。この対応により、強化ファインマン・グラフとバタニン／バーガー半グラフの相互変換ができます。

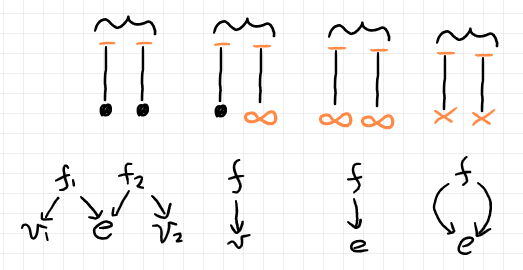
ここからは形式的な定義を述べます。有限圏 $`G`$ が（バタニン／バーガーの意味で）半グラフ〈semi-graph〉であるとは：

対象の集合 $`|G|`$ が3つの部分に直和分割されている； $`|G| = V + F + E`$
$`\phi : x \to y \In G`$ が恒等射でない射ならば、$`x\in F`$ かつ $`y \in (V + E)`$ である。この形の射以外は（恒等射しか）存在しない。
以下を満たす。
1. $`e \in E`$ に入る（恒等射以外の）射はちょうど2本である。上記の二番目の条件から、その2本の射は $`f_1 \to e \leftarrow f_2 \text{ for some }f_1, f_2\in F`$ （コスパン）と書ける。
2. $`f\in F`$ から出る（恒等射以外の）射は1本か2本のどちらかで、次のいずれかの形をしている。
  1. ケース1：出る射が1本だけで $`f \to e \text{ for some } e\in E`$
  2. ケース2：出る射が1本だけで $`f \to v \text{ for some } v\in V`$
  3. ケース3：出る射が2本あり $`f \to e, f \to v \text{ for some }e\in E, v\in V`$
  4. ケース4：出る射が2本あり $`f \to e, f \to e \text{ for some }e \in E`$ （射の平行対）

$`V, F, E`$ に含まれる対象をそれぞれ、頂点〈vertex〉、フラグ〈flag〉、辺〈edge〉と呼びます。$`G`$ の恒等射以外の射は半グラフの接続関係〈incidence relation〉を記述しているので、接続射〈incidence morphism〉と呼んでいいでしょう。

バタニン／バーガーの意味での辺（$`E`$ に含まれる対象）には開放辺は含まれていません。フラグと頂点だけで開放辺を表現します。通常の意味での辺は、$`E`$ の要素（対象）またはケース2のフラグです。ケース2のフラグは、ボリソフ／マニンの定義ではテール〈tail〉です。例外辺と例外ループは $`E`$ の要素（対象）としてエンコードされます。

バタニン／バーガーの用語では、$`f_1 \to e \leftarrow f_2`$ という接続射のコスパンがあると、フラグ $`f_1`$ と $`f_2`$ は隣接している〈adjacent〉といいます。ペアリング対合を使う定義で言えば、$`f_1, f_2`$ はペア〈カップル〉で辺 $`e`$ を構成します。

定義のケース1、ケース2であるフラグ $`f`$ を自由フラグ〈free flag〉と呼びます。自由フラグは、通常の用語法での外部辺に対応します。外部へのインターフェースを提供するものです。

定義のケース2のフラグは$`v`$-フラグ〈$`v`$-flag〉と呼びます。頂点に接続しているフラグの頂点は、ケース2の接続射から一意的に決まります。

辺 $`e\in E`$ が内部辺〈internal edge〉であるとは、次のどちらかが成立することです。

コスパン $`f_1 \to e \leftarrow f_2`$ において、$`f_1 = f_2`$ である。（例外ループ）
次の形の射のジグザグがある。$`v_1 \leftarrow f_1 \to e \leftarrow f_2 \to v_2`$ （通常辺、自己ループ辺含む）

内部辺以外の辺が外部辺〈external edge〉と定義されています。「辺」を $`E`$ の要素と解釈すると、ケース1の $`e`$ だけが外部辺（例外外部辺）です。しかし、ケース2も外部辺とみなしているようです。例えば、以下のカローラの定義における「外部辺」はケース2のフラグのことです。このあたりの概念と呼び名はイマイチすっきりしません。

自由生活辺、自由生活ループ、付点ループ、カローラは、半グラフの構成素ではなくて、ひとつの半グラフとして定義します。