ガーッ! また左と右が。カン拡張 - 檜山正幸のキマイラ飼育記 (はてなBlog)

以前、「カン拡張における上下左右：入門の前に整理すべきこと」というけっこう長い記事を書いたにもかかわらず、 -- にもかかわらずですね、カン拡張の左と右の定義を忘れた。どっちが左でどっちが右か分からなくなった。ハァ(ため息)。

カン拡張の左と右って、「根拠なき選択」なんですよね。左（resp. 右）カン拡張を「左」（resp. 「右」）と呼ぶべき必然性はどこにもないから覚えられないのです。必然性なき選択ですわ。

となると、なんかにコジツケて覚えるしかないです。コジツケ方の話をします。

内容：

左カン拡張と右カン拡張
随伴の左右と結びつける

左カン拡張と右カン拡張

最初に、「カン拡張における上下左右：入門の前に整理すべきこと」に載せていた、拡張／持ち上げの状況を表すストリング図を再掲。黒が与えられた圏・関手で、赤が拡張／持ち上げとなる関手・自然変換です。

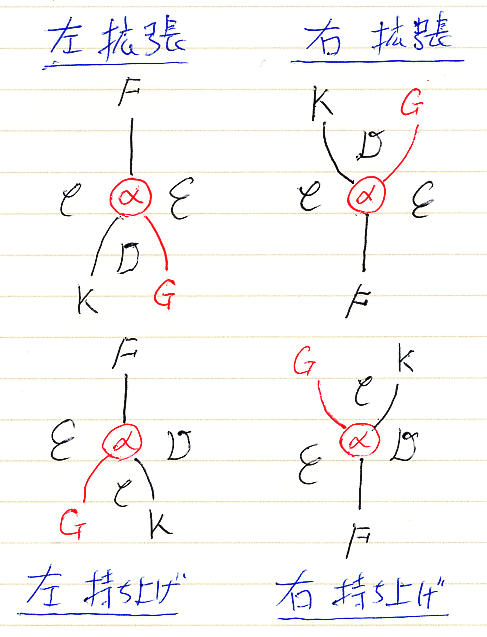
同じことをペースティング図でも書いておけば：

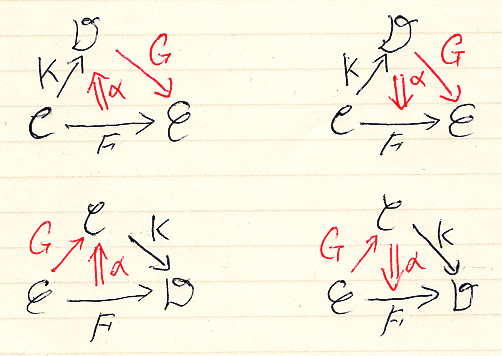
最近使い始めた、MathJaxで描く貧相なペースティング図なら：

$`\require{AMScd}
\newcommand{\hyph}{\mbox{-}}%
\newcommand{\cat}[1]{{\mathcal {#1}}}%
\newcommand{\incat}{\:\: \mbox{in}\:}%
\newcommand{\NE}{\nearrow\!\!\!\nearrow} %
\newcommand{\NW}{\nwarrow\!\!\!\nwarrow} %
\newcommand{\SE}{\searrow\!\!\!\searrow} %
\newcommand{\SW}{\swarrow\!\!\!\swarrow} %
%
\begin{CD}
\cat{D} @>{G}>> {} @= \cat{E} \\
@A{K}AA @.{\NW\alpha} @| \\
\cat{C}@= {} @>>{F}> \cat{E} \\
\end{CD} \\
\:\\
\begin{CD}
\cat{D} @>{G}>> {} @= \cat{E} \\
@A{K}AA @.{\SE\alpha} @| \\
\cat{C}@= {} @>>{F}> \cat{E} \\
\end{CD} \\
\:\\
\begin{CD}
\cat{E} @= {} @>{G}>> \cat{C} \\
@| @.{\NE\alpha} @VV{K}V \\
\cat{E} @>{F}>> {} @= \cat{D} \\
\end{CD} \\
\:\\
\begin{CD}
\cat{E} @= {} @>{G}>> \cat{C} \\
@| @.{\SW\alpha} @VV{K}V \\
\cat{E} @>{F}>> {} @= \cat{D} \\
\end{CD} \\
`$

以上は、カンとは限らない一般的な拡張／持ち上げの状況です。持ち上げはあまり使わないので、以下では拡張だけ扱います。

関手のあいだの自然変換が存在することを不等号'≦'で略記することにします。

F ≦ G :⇔ (FからGに向かう自然変換が在る)

この記法で、Gが、Kに沿ったFの左拡張であることは F ≦ K＊G と書けます。ここで、'＊'は関手の図式順結合記号です。左拡張Lが、この不等号に関する“最小性”を持つことは次のように書けます。

F ≦ K＊G ならば、L ≦ G

これは、Lが左拡張のなかでは最小であることを主張しています。Lが左カン拡張である条件がこれです。同様な書き方で、

K＊G ≦ F ならば、G ≦ R

これは「Rが右拡張のなかで最大である」こと -- 右カン拡張の条件です。

不等号で書いてみると、左拡張を優拡張、右拡張を劣拡張と呼びたくなります。（「順序集合のカン拡張と特徴述語論理」でそう呼んでます。）

優拡張のなかで最小のもの（最小優拡張）が、カン優拡張
劣拡張のなかで最大のもの（最大劣拡張）が、カン劣拡張

とかなら、まだしも覚えやすかったのだけど、実際は何の連想も働かない左と右、どうコジツケましょうか？

随伴の左右と結びつける

随伴の左右と結びつけることにします。随伴に関しては、左右の定義を覚えてます（僕は）。これもコジツケで覚えてるのですが、今日はそのコジツケの話はしないで、ともかくも「随伴の左右は知ってるよ」を前提します*1。

Lが、Kに沿ったFの左カン拡張（最小優拡張）であることを次のように書きましょう。

   F ≦ K＊G in [C, E]
 -----------------------↓↑
   L ≦ G in [D, E]

この意味は：

不等号 ≦ は、既に説明したとおりです。
[C, E] と [D, E] は関手圏です。
右端の ↓↑ は、上から下、下から上の両方向の推論が出来ることです。
つまり、不等号の根拠となる自然変換のあいだに1：1の対応があります。

これをホムセットの同型として書けば：

[C, E](F, K＊G) $`\cong`$ [D, E](L, G)

Lが、Kを固定した上でFから決まるとすれば、L = L_K(F) と書けます。

[C, E](F, K＊G) $`\cong`$ [D, E](L_K(F), G)

関手Kによる前結合引き戻しを K^*:[D, E]→[C, E] とすると、上のホムセット同型は、次の随伴関係を示唆します。

L_K -| K^*

実際に、L_KとK^*は随伴で、L_Kが随伴系の左関手になります。

オオーッ、左と左が一致した！ 次のように覚えましょう。

前結合引き戻し関手K^*の左随伴関手が、左カン拡張関手である。

同様に、

前結合引き戻し関手K^*の右随伴関手が、右カン拡張関手である。

これで覚えられるのかなぁ？

*1:随伴に関しては、「圏論の随伴をちゃんと抑えよう」参照。