随伴系とカン拡張

随伴系〈adjunction | adjoint system〉は既に知られているとして、随伴系をカン拡張の枠組みで解釈できるでしょうか？ できます。やってみます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{－} }
\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
\require{color} % 緑色
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }%
\newcommand{\For}{\Keyword{For } }%
%\newcommand{\Define}{\Keyword{Define } }%
\newcommand{\Where}{\Keyword{Where } }%
%\newcommand{\Subject}{\Keyword{Subject } }%
\newcommand{\iexcl}{ \style{display: inline-block; transform: rotate(180deg)}{!} }% inverted excl.
`$

内容：

はじめに

この記事の表題とリードパラグラフは、「米田の補題と左カン拡張」のそれと同じテンプレートです。意図も同じです。随伴系についてあらためて説明する記事ではなくて、「カン拡張を事例で理解しよう」の事例として随伴系を使います。「米田の補題と左カン拡張」の続きだと思ってください。

右カン拡張 $`\mrm{Ran}_K F`$ と 左カン拡張 $`\mrm{Lan}_K F`$ は、次のような自然なホムセット同型によって定義されました。

$`\For K:\cat{C} \to \cat{D} \In {\bf CAT}\\
\For F: \cat{C} \to \cat{E} \In {\bf CAT}\\
\quad [\cat{C},\cat{E}](K*\hyp, F) \cong [\cat{D}, \cat{E}](\hyp, \mrm{Ran}_K F) \:\text{ natural in }\hyp, F\\
\quad [\cat{C},\cat{E}](F, K*\hyp) \cong [\cat{D}, \cat{E}](\mrm{Lan}_K F, \hyp) \:\text{ natural in }\hyp, F
`$

この自然なホムセット同型達は、次のような随伴トリプルを定義します。

$`\quad \mrm{Lan}_K \dashv (K*\hyp) \dashv \mrm{Ran}_K`$

カン拡張の定義に随伴の概念を使っていたので、随伴系をカン拡張の枠組みで解釈したら循環論法ではないのか？ 確かに、様々な定義が循環してますが、議論の出発点や流れを変えることで生じる循環なので、それで矛盾が起きるとかではないです。別に循環してもかまいません。むしろ、概念の整合性や有効性を相互に担保しあうことになります。

右カン拡張と左カン拡張

右カン拡張は、$`K, F`$ を固定した柱体の圏 $`\mrm{Cyl}_{K, F}`$ の終対象だと考えます。圏 $`\mrm{Cyl}_{K, F}`$ の対象は次のように書けます。

$`\quad (G, \alpha) \\
\Where \alpha:: K*G \twoto F :\cat{C} \to \cat{E} \In {\bf CAT}`$

もうひとつの柱体 $`(G', \alpha')`$ があったとき、そのあいだの射は次のように書けます。

$`\quad (\sigma, e) : (G, \alpha) \to (G', \alpha') \In \mrm{Cyl}_{K, F}\\
\Where \\
\quad \alpha :: K*G \twoto F :\cat{C} \to \cat{E} \In {\bf CAT}\\
\quad \alpha' :: K*G' \twoto F :\cat{C} \to \cat{E} \In {\bf CAT}\\
\quad \sigma :: G \twoto G' : \cat{D} \to \cat{E} \In {\bf CAT}\\
\quad e ::: \alpha = (K*\sigma) ; \alpha' :: K*G \twoto F : \cat{C} \to \cat{E} \In {\bf CAT}
`$

柱体のあいだの射は、次のような記号の乱用で記述します。

$`\quad \sigma = (\sigma, \mrm{Eq}\,\sigma) \;: (G, \alpha) \to (G', \alpha') \In \mrm{Cyl}_{K, F}`$

文字 $`\sigma`$ が、射とその自然変換パートの両方を意味します（乱用オーバーロード）。

一般に、圏に終対象があるとき、終対象への唯一の射を $`!_X`$ のように感嘆符で書きます。$`\mrm{Cyl}_{K, F}`$ の場合も同じ記法を使うと、終対象である右カン拡張への射は次のように書けます。$`\alpha = (G, \alpha)`$ という略記も使っています。

$`\quad !_{\alpha} = (!_{\alpha}, \mrm{Eq}\,!_{\alpha}) \;: (G, \alpha) \to (R, \rho) \In \mrm{Cyl}_{K, F}\\
\Where \\
\quad \alpha :: K*G \twoto F :\cat{C} \to \cat{E} \In {\bf CAT}\\
\quad \rho :: K*R \twoto F :\cat{C} \to \cat{E} \In {\bf CAT}\\
\quad !_\alpha :: G \twoto R : \cat{D} \to \cat{E} \In {\bf CAT}\\
\quad \mrm{Eq}\,!_\alpha ::: \alpha = (K* !_\alpha) ; \rho :: K*G \twoto F : \cat{C} \to \cat{E} \In {\bf CAT}
`$

左カン拡張の場合は双対的になります。$`K, F`$ を固定した余柱体の圏 $`\mrm{Cocyl}_{K, F}`$ の始対象が左カン拡張です。圏 $`\mrm{Cocyl}_{K, F}`$ の対象は次のように書けます。

$`\quad (G, \beta) \\
\Where \beta::F \twoto K*G :\cat{C} \to \cat{E} \In {\bf CAT}`$

もうひとつの余柱体 $`(G', \beta')`$ があったとき、そのあいだの射は次のように書けます。

$`\quad (\tau, e) : (G, \beta) \to (G', \beta') \In \mrm{Cocyl}_{K, F}\\
\Where \\
\quad \beta::F \twoto K*G :\cat{C} \to \cat{E} \In {\bf CAT}\\
\quad \beta'::F' \twoto K*G' :\cat{C} \to \cat{E} \In {\bf CAT}\\
\quad e ::: \beta;K*\tau = \beta' :: K*G \twoto F : \cat{C} \to \cat{E} \In {\bf CAT}
`$

余柱体のあいだの射は、次のような記号の乱用で記述します。

$`\quad \tau = (\tau, \mrm{Eq}\,\tau) : (G, \beta), (G', \beta') \In \mrm{Cocyl}_{K, F}`$

一般に、圏に始対象があるとき、始対象からの唯一の射を $`\iexcl_X`$ のように逆感嘆符で書きます*1。右カン拡張と同様な略記を使って、始対象である左カン拡張からの射は次のように書けます。

$`\quad \iexcl_{\beta} = (\iexcl_{\beta}, \mrm{Eq}\, \iexcl_{\beta}) \;: (L, \lambda) \to (G, \beta) \In \mrm{Cocyl}_{K, F}\\
\Where \\
\quad \lambda :: F \twoto K*L :\cat{C} \to \cat{E} \In {\bf CAT}\\
\quad \beta :: F \twoto K*G :\cat{C} \to \cat{E} \In {\bf CAT}\\
\quad \iexcl_\beta :: L \twoto G : \cat{D} \to \cat{E} \In {\bf CAT}\\
\quad \mrm{Eq}\,\iexcl_\beta ::: \lambda ; (K* \iexcl_\beta) = \beta :: F \twoto K*G : \cat{C} \to \cat{E} \In {\bf CAT}
`$

「米田の補題と左カン拡張」においては、$`\beta = (G, \beta)`$ から決まる $`\iexcl_\beta`$ を次のように書きました。

$`\quad \iexcl_\beta = (\iexcl_\beta, \mrm{Eq}\, \beta) = (\beta^\sharp, e_\beta)`$

右随伴関手は左カン拡張

次のような随伴系があるとします。使っている構成素ラベル（随伴系の構成素に割り当てる記号）は、「代数的な随伴系から自然なホムセット同型へ」と同じです。

$`%
\quad F:\cat{C} \to \cat{D} \In {\bf CAT} \\
\quad G:\cat{D} \to \cat{C} \In {\bf CAT} \\
\quad \eta:: \mrm{Id}_{\cat{C}} \twoto F*G : \cat{C} \to \cat{C} \In {\bf CAT} \\
\quad \varepsilon :: G*F \twoto \mrm{Id}_{\cat{D}} : \cat{D} \to \cat{D} \In {\bf CAT} \\
\quad \Gamma ::: (\eta * F);(F * \varepsilon) = \mrm{ID}_F :: F\twoto F : \cat{C} \to \cat{D}
\In {\bf CAT}\\
\quad \Delta ::: (G*\eta); (\varepsilon * G) = \mrm{ID}_G :: G\twoto G : \cat{D} \to \cat{C}
\In {\bf CAT}
`$

これら一式は、次のような絵〈ストリング図〉に描けます。描画方向は上から下、左から右です。

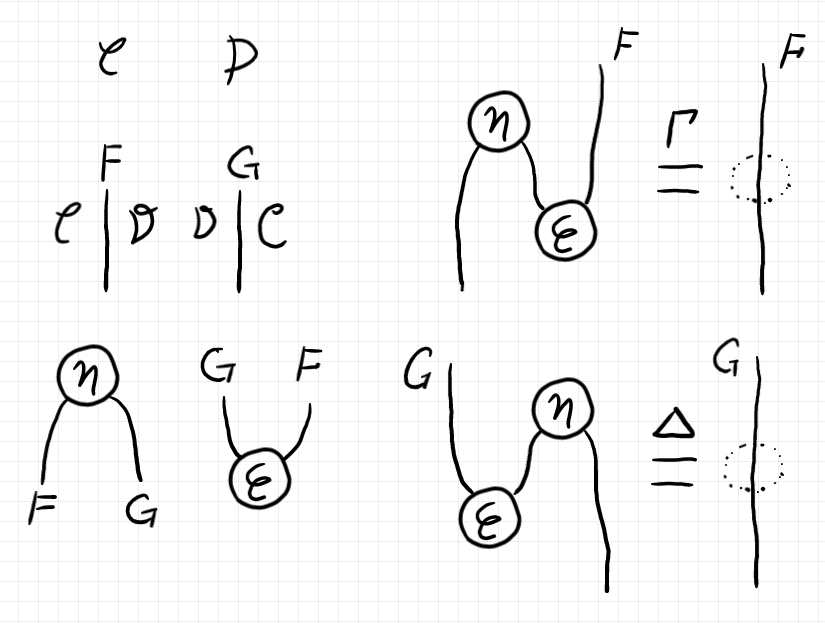
「米田の補題と左カン拡張」で書いたように、とある構造／系をカン拡張のフレームワークで表すとは、一般論と事例で使われている記号ラベルのあいだのパターンマッチングをすることです。以下に、記号ラベルの当てはめ〈パターンマッチング〉を一覧表で示します。一般論が左カン拡張で、事例が随伴系です。

$`\text{一般論}`$	$`\text{事例}`$	$`\text{事例への備考}`$
$`\cat{C}`$	$`\cat{C}`$	一般的な圏
$`\cat{D}`$	$`\cat{D}`$	一般的な圏
$`\cat{E}`$	$`\cat{C}`$	同じ圏
$`K`$	$`F`$	左随伴関手（先に与える）
$`F`$	$`\mrm{Id}_\cat{C}`$	恒等関手
$`L`$	$`G`$	右随伴関手（後から決まる）
$`\lambda`$	$`\eta`$	随伴系の単位

この当てはめによって、与えられた関手 $`F`$ （左カン拡張フレームワークの形状関手 $`K`$ に相当）と与えられた恒等関手 $`\mrm{Id}_\cat{C}`$ に対して左カン拡張を作ると（それが出来たとして）、左カン拡張関手は $`F`$ の右随伴関手となり、余柱体変換は随伴系の単位を与えることになります。

記号の乱用を使って書けば、次のようです。

$`\quad \mrm{Lan}_F \,\mrm{ID}_\cat{C} = (\mrm{Lan}_F\, \mrm{ID}_\cat{C}, \lambda) = (G, \eta)`$

左随伴関手は右カン拡張

前節では、随伴系の左関手が与えられて、それに対して左カン拡張の構成手続きによって、随伴系の右関手〈右随伴関手〉と随伴系の単位を定義しました。先に、随伴系の右関手を与えて、それに対して右カン拡張の構成手続きによって、随伴系の左関手〈左随伴関手〉と随伴系の余単位を定義することもできます。

以下に、記号ラベルの当てはめ〈パターンマッチング〉を一覧表で示します。一般論が右カン拡張で、事例が随伴系です。

$`\text{一般論}`$	$`\text{事例}`$	$`\text{事例への備考}`$
$`\cat{C}`$	$`\cat{C}`$	一般的な圏
$`\cat{D}`$	$`\cat{D}`$	一般的な圏
$`\cat{E}`$	$`\cat{D}`$	同じ圏
$`K`$	$`G`$	右随伴関手（先に与える）
$`F`$	$`\mrm{Id}_\cat{D}`$	恒等関手
$`R`$	$`F`$	左随伴関手（後から決まる）
$`\rho`$	$`\varepsilon`$	随伴系の余単位

この当てはめによって、与えられた関手 $`G`$ （左カン拡張フレームワークの形状関手 $`K`$ に相当）と与えられた恒等関手 $`\mrm{Id}_\cat{D}`$ に対して右カン拡張を作ると（それが出来たとして）、右カン拡張関手は $`G`$ の左随伴関手となり、柱体変換は随伴系の余単位を与えることになります。

記号の乱用を使って書けば、次のようです。

$`\quad \mrm{Ran}_G \,\mrm{ID}_\cat{D} = (\mrm{Ran}_G\, \mrm{ID}_\cat{D}, \rho) = (F, \varepsilon)`$

構造／系と考えた左カン拡張は、構造／系と考えた随伴系を包摂することが分かりました。双対的な手法で、右カン拡張も随伴系を包摂します。構造／系のあいだの包摂関係は、記号ラベルのパターンマッチングで了解できるわけで、名前の置き換えって大事です。

*1:逆感嘆符が書けない環境も多いので、僕は通常 $`\theta_X`$ を使っています。今回の逆感嘆符は、CSSによる180度回転を使っているので、うまく表示されない場合があるかも知れません。