一応書き終わってはいるのですがまだ投稿してないブログ記事があります。そのなかで、ちゃんと定義するのがめんどうなので雰囲気的な説明だけした上で、“生〈なま〉の2-関手”と“生〈なま〉の2-自然変換”という言葉を使っています。気持ちとしては、「料理の素材だけど調理してないからそのままでは食べられない、だから生〈raw | uncooked〉」です。
雰囲気と気持ちだけではどうにもならないので、当該の記事を投稿する前に、“生〈なま〉”なモノについて説明することにします。なお、「生の◯◯◯」という呼び名がいいとは思ってないので、いずれ変更するかも知れません。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
%\newcommand{\msf}[1]{\mathsf{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\pipe}{\mid }
\newcommand{\In}{\text{ in } }
%\newcommand{\Imp}{ \Rightarrow }
%\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{-} }
%\newcommand{\op}{\mathrm{op} }
\newcommand{\id}{\mathrm{id} }
%\newcommand{\pto}{ \supseteq\!\to }
%\newcommand{\u}[1]{\underline{#1}}
\newcommand{\rto}[1]{\;_{#1}\!\!\not\to }
\newcommand{\rtwoto}[1]{\;_{#1}\!\!\not\Rightarrow }
`$
内容:
2-圏
$`\cat{K}, \cat{L}`$ などは(必ずしも厳密とは限らない)小さい2-圏だとします*1。次の約束をします。
- 2-圏 $`\cat{K}`$ の対象〈0-射〉の集合を $`|\cat{K}|`$ と書く。$`|\cat{K}|`$ の要素〈対象 | 0-射〉は、ラテン文字小文字 $`a, b`$ などで表す。
- 2-圏 $`\cat{K}`$ の射〈1-射〉の集合を $`|\cat{K}|_1`$ と書く。$`|\cat{K}|_1`$ の要素〈射 | 1-射〉は、ラテン文字小文字 $`f, g`$ などで表す。
- 2-圏 $`\cat{K}`$ の2-射の集合を $`|\cat{K}|_2`$ と書く。$`|\cat{K}|_2`$ の要素〈2-射〉は、ギリシャ文字小文字 $`\phi, \psi`$ などで表す。
- 1-射と1-射、または2-射と2-射、または1-射と2-射の横結合は、図式順演算子記号 '$`*`$'(アスタリスク)で書く。
- 2-射と2-射の縦結合は、図式順演算子記号 '$`;`$'(セミコロン)で書く。
$`a, b\in |\cat{K}|`$ に対して、$`a, b`$ が定めるホム圏を $`\cat{K}(a, b)`$ と書きます。次は同じことです。
- $`f: a \to b \In \cat{K}`$ ($`f`$ は $`\cat{K}`$ 内の1-射)
- $`f \in |\cat{K}(a, b)|`$ ($`f`$ はホム圏 $`\cat{K}(a, b)`$ の対象)
$`f, g\in |\cat{K}(a, b)|`$ に対して、$`f, g`$ が定めるホムセット(ホム圏のホムセット)を $`\cat{K}(a, b)(f, g)`$ と書きます。次は同じことです。
- $`\varphi :: f\twoto g: a \to b \In \cat{K}`$ ($`\varphi`$ は $`\cat{K}`$ 内の2-射)
- $`\varphi : f \to g \In \cat{K}(a, b)`$ ($`\varphi`$ はホム圏 $`\cat{K}(a, b)`$ の射)
- $`\varphi \in \cat{K}(a, b)(f, g)`$ ($`\varphi`$ はホム圏 $`\cat{K}(a, b)`$ のホムセットの要素)
2-圏の対象集合は集合で、ホム圏は圏で、ホム圏の対象集合とホムセットは集合ですから、次が成立します。$`\cat{K}`$ は小さいと仮定していることに注意してください。
- $`|\cat{K}| \in |{\bf Set}|`$
- $`\forall a, b\in |\cat{K}|.\, \cat{K}(a, b) \in |{\bf Cat}|`$
- $`\forall a, b\in |\cat{K}|.\, |\cat{K}(a, b)| \in |{\bf Set}|`$
- $`\forall a, b\in |\cat{K}|. \forall f, g \in |\cat{K}(a, b)|.\, \cat{K}(a, b)(f, g) \in |{\bf Set}|`$
この記事では、2-圏を、対象のペアでインデックス付けられたホム圏達だとみなします。もちろん、2-圏の構造はそれだけではないのですが、今回の目的ではホム圏の束〈たば〉*2を考えるだけでも十分です。
生の2-関手と生の2-自然変換
2-圏のあいだの準同型射、準同型射のあいだの準同型射などを定義したいのですが、いきなりちゃんとした定義は難しいので、次の2段階に分けることにします。
- ちゃんとした定義のときに使う素材となる、比較的単純な概念を定義する。
- 定義済みの単純な概念を素材に使って、より複雑な概念を定義する。
今回定義する比較的単純な概念とは、2-圏のあいだの“生の2-関手”と、2つの“生の2-関手”のあいだの“生の2-自然変換”です。
生の2-関手とは、2-圏の対象のペア、または対象のトリプルでインデックス付けられた関手の族〈ファミリー〉です。族の成分〈component〉である各関手は、ホム圏のあいだの関手です。対象のトリプルでインデックス付けられる場合は各成分は二項関手〈双関手〉になります。
生の2-自然変換とは、2つの生の2-関手のあいだを結ぶ、自然変換の族です。生の2-関手が対象のペア、または対象のトリプルでインデックス付けられるので、生の2-自然変換も同様なインデックス付けを持つ族になります。
2インデックスの生の2-関手
$`S`$ が、小さい2-圏 $`\cat{K}`$ から $`\cat{L}`$ への2インデックスの生の2-関手であることを次のように書くことにします。
$`\quad S:\cat{K} \rto{2} \cat{L} \In {\bf 2Cat}`$
矢印の根本の 2 は、2つのインデックスが付くことを示します。矢印に斜線(否定の意味)をかぶせているのは、ほんとは $`{\bf 2Cat}`$ の射ではないことを示します。
さて、ここでやっと 生の2-関手〈raw 2-functor〉 $`S`$ の定義を述べます。$`S`$ は次の構成素からなります。
- 写像 $`S_0 : |\cat{K}| \to |\cat{L}| \In {\bf Set}`$
- 関手の2インデックス族 $`S_1`$
$`a, b \in |\cat{K}|`$ ごとに $`(S_1)_{a, b}: \cat{K}(a, b) \to \cat{L}(S_0(a), S_0(b) ) \In {\bf Cat}`$
下付きインデックスが煩雑なので省略していいとします。
$`\text{For }a \in |\cat{K}|\\
\quad S(a) := S_0(a)\\
\text{For }a, b \in |\cat{K}|,\; f \in |\cat{K}(a, b)|\\
\quad S(f) := S_{a, b}(f) := (S_1)_{a, b}(f) \\
\text{For }a, b \in |\cat{K}|,\; f, g \in |\cat{K}(a, b)|, \; \varphi \in \cat{K}(a, b)(f, g)\\
\quad S(\varphi) := S_{a, b}(\varphi) := (S_1)_{a, b}(\varphi)
`$
ペースティング図風の絵で描くと次のような感じです。
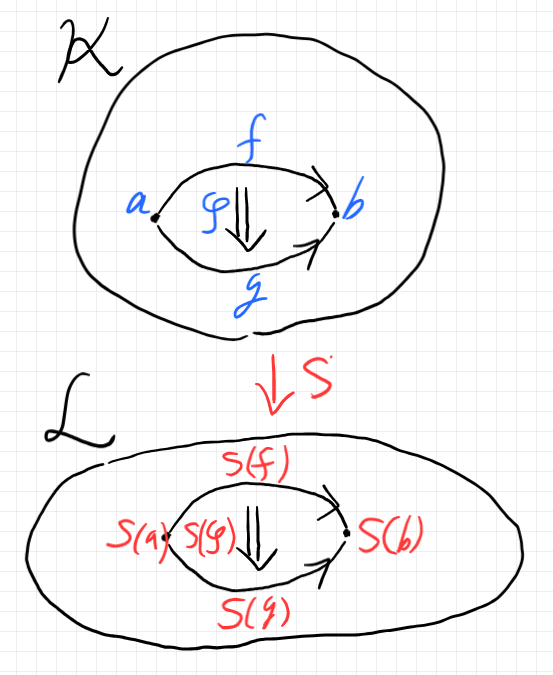
対象のペア $`(a, b)`$ ごとに $`S_{a, b}`$ は関手なので次は成立します。
$`\text{For }f, g, h \in |\cat{K}(a, b)|\\
\text{For }\varphi : f \to g \In \cat{K}(a, b)\\
\text{For }\psi : g \to h \In \cat{K}(a, b)\\
\quad S_{a, b}(\varphi ; \psi) = S_{a, b}(\varphi) ; S_{a, b}(\psi)
`$
$`\text{For }f \in |\cat{K}(a, b)|\\
\quad S_{a, b}(\mrm{vid}_f) = \mrm{vid}_{S_{a, b}(f)}
`$
ここで、$`\mrm{vid}`$ は縦結合〈vertical composition〉の恒等〈identity〉です。$`\mrm{vid}_f`$ は、ホム圏 $`\cat{K}(a, b)`$ 内の恒等1-射ですが、$`\cat{K}`$ 内で見れば2-射です。
生の2-関手は、ホム圏ごとに関手になっていることは要求してますが、その他の条件は何も課していません。例えば、$`f:a\to b, k : b \to c`$ であるとき、横結合に対する値 $`S(f*k)`$ がどうなるかは分かりません。生の2-関手は、2-圏の横方向の情報にまったく無頓着です。ホム圏達がパランパランに分解されてシャフルされても、生の2-関手にとっては痛くも痒くもありません(シャフルを認識できないので)。
3インデックスの生の2-関手
小さい2-圏 $`\cat{K}`$ から $`\cat{L}`$ への3インデックスの生の2-関手 $`T`$ を次のように書くことにします。
$`\quad T : \cat{K} \rto{3} \cat{L} \In {\bf 2Cat}`$
3インデックスの生の2-関手〈raw 2-functor with 3 indexes〉 $`T`$ は次の構成素からなります。
- 写像 $`T_0 : |\cat{K}| \to |\cat{L}| \In {\bf Set}`$
- 二項関手〈双関手〉の3インデックス族 $`T_1`$
$`a, b, c \in |\cat{K}|`$ ごとに $`(T_1)_{a, b, c}: \cat{K}(a, b)\times \cat{K}(b, c) \to \cat{L}(T_0(a), T_0(c) ) \In {\bf Cat}`$
下付きインデックスが煩雑なので省略していいとします。
$`\text{For }a \in |\cat{K}|\\
\quad T(a) := T_0(a)\\
\text{For }a, b, c \in |\cat{K}|,\; f \in |\cat{K}(a, b)|,\; g \in |\cat{K}(b, c)|\\
\quad T(f, g) := T_{a, b, c}(f, g) := (T_1)_{a, b, c}(f, g) \\
\text{For }a, b, c \in |\cat{K}|,\; f, g \in |\cat{K}(a, b)|, \; h, k\in |\cat{K}(b, c)|\\
\text{For } \varphi \in \cat{K}(a, b)(f, g),\; \tau \in \cat{K}(b, c)(h, k)\\
\quad T(\varphi, \tau) := T_{a, b, c}(\varphi, \tau) := (T_1)_{a, b, c}(\varphi, \tau)
`$
ペースティング図風の絵で描くと次のような感じです。
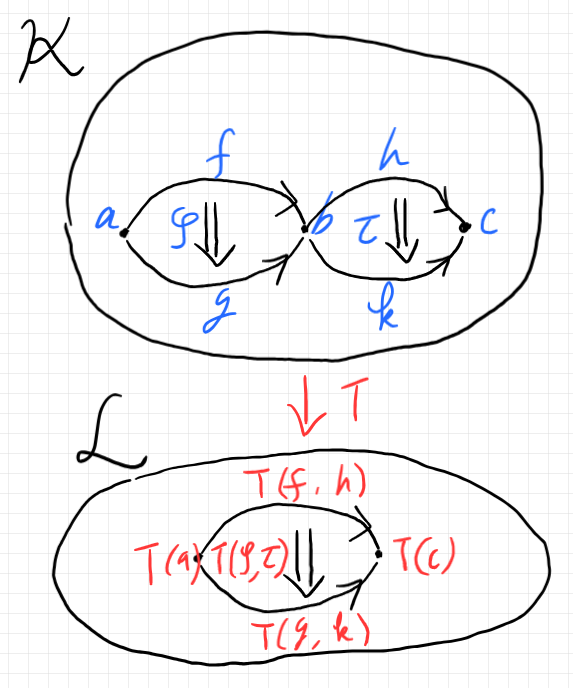
2つのホム圏 $`\cat{K}(a, b)`$ と $`\cat{K}(b, c)`$ は、$`\cat{K}`$ 内で隣接してますが、生の2-関手 $`T`$ はそのことを知りません。3インデックスの場合でも、2-圏の横方向には無頓着です。3インデックスの生の2-関手は、与えられた2つの圏(独立な2つの圏だと認識)に対する二項関手を提供するだけです。3インデックスの生の2-関手の成分〈component〉は二項関手なので、二項関手の条件 -- 例えば交替律〈interchange law〉は満たしています。
2インデックスの生の2-関手は“関手の族”であり、3インデックスの生の2-関手は“二項関手の族”です。となると、1インデックスの生の2-関手は“無項関手の族”となるでしょう。実際、$`a \in |\cat{K}|`$ に $`R(a) \in |\cat{L}|`$ を対応させる写像 $`R`$ は、1インデックスの生の2-関手(無項関手の族)といえます。
実際に使うのが2インデックスと3インデックスというだけで、nインデックスの生の2-関手も定義はできます。それは、対象集合のあいだの写像と、n個のインデックスを持つ(n -1)項関手達の族です(n と (n - 1) とズレるのは植木算の原理です)。
$`\quad P_{a_1, a_2, \cdots, a_n} : \cat{K}(a_1, a_2) \times \cdots \times \cat{L}(a_{n -1},a_n ) \to \cat{K}(P(a_1), P(a_n)) \In {\bf Cat}`$
n = 1, 2, 3 の場合は既に述べたようになります。
多インデックスの生の2-関手〈raw 2-functor with many indexes〉の場合、インデックスの個数を注釈情報として添えたほうが分かりやすいでしょう。
- $`S^{(2)} = (S_0, S_1^{(2)})`$ ($`S`$ は2インデックスの生の2-関手)
- $`T^{(3)} = (T_0, T_1^{(3)})`$ ($`T`$ は3インデックスの生の2-関手)
1インデックスのときも形式を揃えたいなら:
- $`R^{(1)} = (R_0, R_1^{(1)})`$ ($`R`$ は1インデックスの生の2-関手、$`R_1^{(1)} = R_0`$)
関手と自然変換からの準備
今まで、$`\cat{K}`$ や $`\cat{L}`$ は小さい2圏だから $`{\bf 2Cat}`$ の対象だと言ってきました。小さい2圏達が作る“圏” $`{\bf 2Cat}`$ は、実は3-圏です。3-圏 $`{\bf 2Cat}`$ の1-射/2-射/3-射が何であるか、現時点の我々はまったく知りません。生の2-関手が $`{\bf 2Cat}`$ の1-射なのか? というと、そうではありません。そうではないことを明示するため '$`\not\to`$' という矢印記号を使ったのです。
3-圏 $`{\bf 2Cat}`$ の1-射/2-射/3-射をきちんと記述・決定するのは難しい問題で、この記事では扱いません(別な記事で扱う予定)。一方で、小さな圏達の2-圏 $`{\bf Cat}`$ については十分に知っていると仮定しています。2-圏 $`{\bf Cat}`$ の1-射は関手で、2-射は自然変換です。
関手と自然変換に関して幾つか約束をしておきます。2-圏 $`\cat{K}, \cat{L}`$ などが備えている横結合・縦結合と区別するため、関手と自然変換の横結合は '$`\star`$'(黒星印)、自然変換の縦結合は '$`\pipe`$'(パイプ記号)とします。
$`\alpha :: F \twoto G : \cat{C} \to \cat{D} \In {\bf Cat}`$ だとします。このとき、次の図式は可換です。
$`\require{AMScd}\\
\text{For } f:a \to b \In \cat{D}\\
\quad \begin{CD}
F(a) @>{\alpha_a}>> G(a) \\
@V{F(f)}VV @VV{G(f)}V \\
F(b) @>{\alpha_b}>> G(b)
\end{CD}\\
\quad \text{commutative in }\cat{D}
`$
したがって、四角形の対角線の射が一意に決まるので、それを $`\alpha(f)`$ または $`\alpha_f`$ と書きます。
$`\text{For } f:a \to b \In \cat{D}\\
\quad \alpha(f) : F(a) \to G(b) \In \cat{D}`$
$`F(f), \alpha(f), G(f)`$ の関係はストライプ図で描くと分かりやすいです。
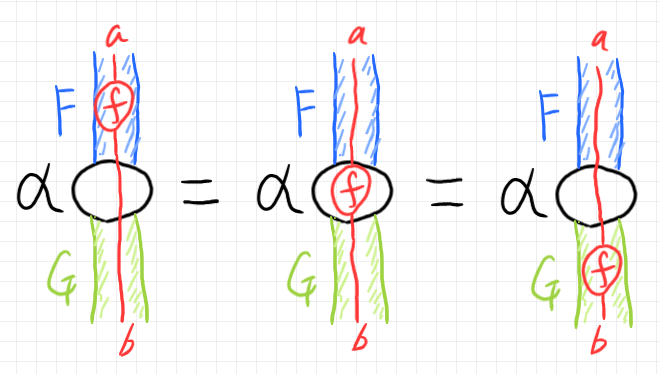
テキストだと、$`\alpha(f)`$ だったり $`\alpha_f`$ だったり、あるいは $`f.\alpha`$(図式順記法)だったりと記法が安定しなくて癪に障るのですが、ストライプ図で見ると、$`\alpha :: F \twoto G`$ によるストライプのなかで射 $`f`$ をスライドさせてもかまわんよ、ってことです。上記の3本のストライプ状況をテキストで書けば:
- $`F(f) * \alpha_b * \id_{G(b)} \In \cat{D}`$
あるいは、ヒゲ結合を許すなら $`F(f) * \alpha_b * G(b) \In \cat{D}`$ - $`\id_{F(a)} * \alpha(f) * \id_{G(b)} \In \cat{D}`$
あるいは、ヒゲ結合を許すなら $`F(a) * \alpha(f) * {G(b)} \In \cat{D}`$ - $`\id_{F(a)} * \alpha_a * G(f) \In \cat{D}`$
あるいは、ヒゲ結合を許すなら $`F(a) * \alpha_a * G(f) \In \cat{D}`$
ストライプ図で描くメリットは:
- $`\alpha(f), \alpha_f, f.\alpha`$ などの記法の違いに苛つくことはない。
- 対象 $`a`$ と恒等射 $`\id_a`$ をいちいち区別しなくてもよい(どちらもストレートワイヤー)。
生の2-自然変換
$`\cat{K}`$ と $`\cat{L}`$ は小さい2-圏とします(i.e. $`\cat{K}, \cat{L} \in |{\bf 2Cat}|`$)。ここからの文脈では、$`S`$ と $`T`$ は、小さい2-圏 $`\cat{K}`$ から $`\cat{L}`$ への2インデックスの生の2-関手であるとします。
$`\quad S :\cat{K} \rto{2} \cat{L} \In {\bf 2Cat}\\
\quad T :\cat{K} \rto{2} \cat{L} \In {\bf 2Cat}
`$
このセットアップで、$`\alpha`$ が $`S`$ から $`T`$ への生の2-自然変換であることを次のように書くことにします。
$`\quad \alpha :: S \rtwoto{2} T : \cat{K} \rto{2} \cat{L} \In {\bf 2Cat}`$
生の2-自然変換は2-射っぽいので二重矢印にしています。根本の 2 はそれとは別で、インデックスの個数が2つであることを示します。生の2-自然変換は、3-圏 $`{\bf 2Cat}`$ のほんとの2-射ではないので、否定の斜線をかぶせています。
2インデックスの生の2-自然変換〈raw 2-natural transformation with 2 indexes〉 $`\alpha`$ も2つの構成素〈パート〉からなります。
- 写像 $`\alpha_0 : |\cat{K}| \to |\cat{L}|_1 \In {\bf Set}`$ 。これは、次の意味で $`S_0`$ から $`T_0`$ への“変換”になっている。
$`\text{For }a \in |\cat{K}|\\ \quad\alpha_0(a) : S(a) \to T(a)\In \cat{L}`$ - 自然変換の2インデックス族 $`\alpha_1`$
$`a, b \in |\cat{K}|`$ ごとに
$`(\alpha_1)_{a, b}:: S_{a, b} \star \alpha_0(b)_* \twoto \alpha_0(a)^* \star T_{a, b} : \cat{K}(a, b) \to \cat{L}(S(a), T(b)) \In {\bf Cat}`$
下付きインデックスが煩雑なので適宜省略していいのは今まで同じです。
この定義をいきなり見ても分かりにくいでしょうから、順番にほぐしていきましょう。
$`\alpha_0`$ は、0-射の集合 $`|\cat{K}|`$ から1-射の集合 $`|\cat{L}|_1`$ への写像です。「0-射 to 0-射」の写像であった $`S`$ と $`T`$ を繋ぐ役割りを担います。うまく繋がるための条件が次です。
$`\quad \forall a \in |\cat{K}|.\, \alpha_0(a) : S_0(a) \to T_0(a) \In \cat{L}`$
$`\alpha_0`$ は、自然変換から自然性〈naturality〉を抜いたものです。こういう自然性抜き自然変換に名前がなくて困っている、という話は何度かしたことがあります。例えば次の過去記事。
今回話題にしているような、変換手性〈transforiality〉を完全には満たさない中途半端なヤツラの系統的理論があれば色々と随分楽になると思うのですが、中途半端なヤツラは毛嫌いされているので名前さえありません。
次に、$`\alpha_0(a)^*,\; \alpha_0(b)_*`$ という記号について説明します。これは、(圏のあいだのちゃんとした)関手を表します。$`\alpha_0(a)`$ は前の段落で説明したように、$`\cat{L}`$ の1-射となります。
$`\quad \alpha_0(a) : S(a) \to T(a) \In \cat{L}`$
この1-射 $`\alpha_0(a)`$ から次のプロファイル(域と余域の仕様)の関手を作り出せます。
$`\quad \cat{L}(T(a), T(b)) \to \cat{L}(S(a), T(b)) \In {\bf Cat}`$
その関手とは:
$`\quad |\cat{L}(T(a), T(b))| \ni f \mapsto \alpha_0(a) * f \in |\cat{L}(S(a), T(b))|\\
\quad |\cat{L}(T(a), T(b))|_1 \ni \varphi \mapsto \alpha_0(a) * \varphi \in |\cat{L}(S(a), T(b))|_1
`$
$`\alpha_0(a) * \varphi`$ のなかの '$`*`$'($`\cat{L}`$ の横結合)は、1-射と2-射のヒゲ結合〈whiskering〉です。これはつまり、1-射 $`\alpha_0(a)`$ をプレ結合することにより得られる引き戻し関手です。
$`\quad \alpha_0(a)^* : \cat{L}(T(a), T(b)) \to \cat{L}(S(a), T(b)) \In {\bf Cat}`$
同様に、以下の1-射をポスト結合することにより押し出し関手を作れます。
$`\quad \alpha_0(b) : S(b) \to T(b) \In \cat{L}`$
押し出し関手:
$`\quad \alpha_0(b)_* : \cat{L}(S(a), S(b)) \to \cat{L}(S(a), T(b)) \In {\bf Cat}`$
$`\alpha_0(a)^*,\; \alpha_0(b)_*`$ は関手なので他の関手と(関手の)横結合ができます。以下の表現は、それぞれ関手を表します。
$`\quad S_{a, b} \star \alpha_0(b)_* : \cat{K}(a, b) \to \cat{L}(S(a), T(b)) \In {\bf Cat}\\
\quad \alpha_0(a)^* \star T_{a, b} : \cat{K}(a, b) \to \cat{L}(S(a), T(b)) \In {\bf Cat}
`$
ここまでの説明を前提にすれば、自然変換の2インデックス族 $`\left( (\alpha_1)_{a, b}\right)_{a, b \in |\cat{K}|}`$ の意味は解釈可能なはずです。とはいえ、だいぶシチメンドクサイので、図示の方法を次節で紹介します。
ストライプ図とストリング図
次のようなストライプ図のテンプレートを準備しておきます。
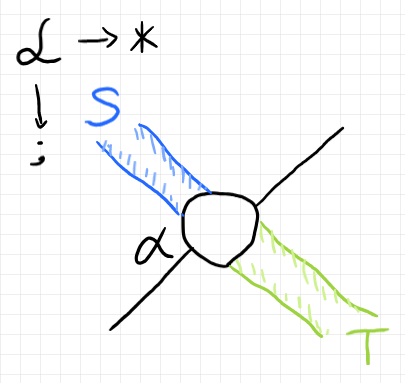
テンプレートのキャンバスは2-圏 $`\cat{L}`$ です。描画方向は、左から右が横結合「$`*`$」の方向、上から下が縦結合「$`;`$」の方向です。青いストライプは生の2-関手 $`S`$ を表し、緑のストライプは生の2-関手 $`T`$ を表します。黒は生の2-自然変換 $`\alpha`$ です。黒い線が $`\alpha_0`$ で黒いマルは $`\alpha_1`$ です。
2-圏 $`\cat{K}`$ 内の1-射 $`f:a \to b \In \cat{K}`$ を選びます。$`\cat{K}`$ が($`\cat{L}`$ もですが)2-圏なので、0-射〈対象〉がエリアで1-射はワイヤーになります。キャンバスとなる圏の次元により、エリア/ワイヤー/ボックス〈ノード〉の意味は変わりますから注意。
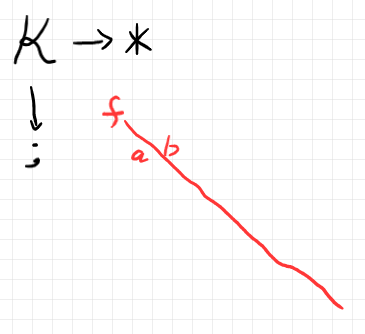
この1-射 $`f`$ をテンプレートのストライプ内にはめ込みます(テンプレートの具体化)。すると、次のようになります。
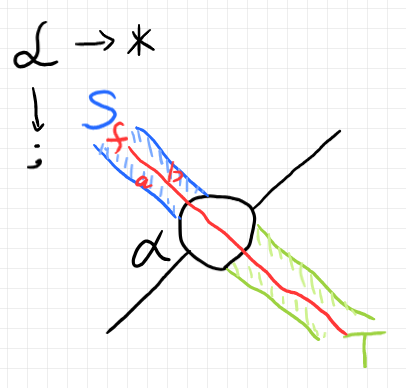
この具体化により、エリア、ワイヤー、ボックス〈ノード〉なども具体化されるので、ラベルを書き込みましょう。
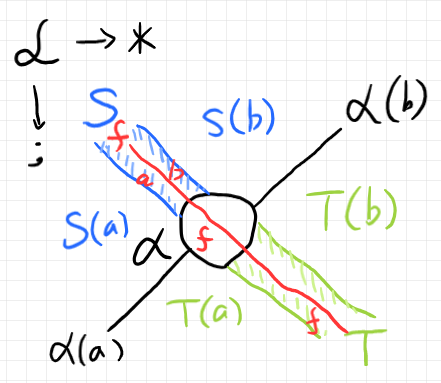
この絵を上下に分割して、上段を辿ってみると次のようです。
$`\quad S(a) \overset{S(f)}{\to} S(b) \overset{\alpha(b)}{\to} T(b) : S(a) \to T(b) \In \cat{L}`$
下段は次のようです。
$`\quad S(a) \overset{\alpha(a)}{\to} T(a) \overset{T(f)}{\to} T(b) : S(a) \to T(b) \In \cat{L}`$
中央の白抜き黒丸は2-射 $`\alpha(f)`$ なので、このプロファイルを書けば次のようです。
$`\quad \alpha(f) :: S(f) * \alpha(b) \twoto \alpha(a) * T(f) : S(a) \to T(b) \In \cat{L}`$
鬱陶しくなりますが、インデックスを完全に付けて書くと:
$`\quad (\alpha_1)_{a, b}(f) :: (S_1)_{a, b}(f) * \alpha_0(b) \twoto \alpha_0(a) * (T_1)_{a, b}(f) : S_0(a) \to T_0(b) \In \cat{L}`$
ストライプの幅やボックスの広がりを潰してストリング図にしてみましょう。例えば次のようになります。
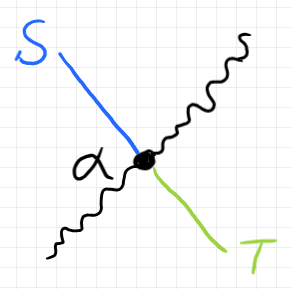
生の2-自然変換の0パートである $`\alpha_0`$ はストライプを潰したものではない(もともと幅がない)ので、波線にしています。波線と黒いドットが一体となってひとつの生の2-自然変換を表します。このような描画法を使うと、生の2-関手と生の2-自然変換が混じった法則を記述するのがとても簡単になります。以下の図は、とある法則を表しています。
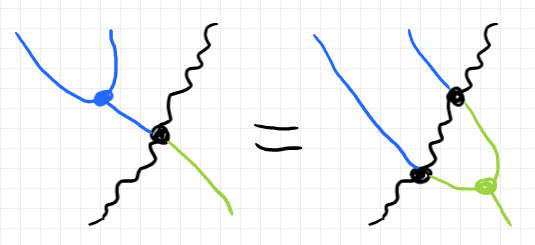
生の◯◯◯ → ?
生の2-自然変換は、2インデックスの場合だけ扱いましたが、3インデックスでも同様な扱いができます。様々なインデックスの個数の生の2-関手と2-自然変換の色々な組み合わせができます。そのような組み合わせの計算があまり注目も言及もされないのは残念です。
そもそも「生の◯◯◯」という呼び名も、合意された名前がないから苦し紛れに使っているわけです。有り体に言って、「生の◯◯◯」の仲間達は出来そこないの変換手〈transfor〉達です。あまりにも膨大な有象無象の群れなのでネーミングしにくいのは確かです。しかし、役立つヤツラもいるわけで、名前を付けてあげたいなー。