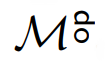大域米田の補題などを扱う場合は、関手や自然変換の向きに注意する必要があります。向きをどんな約束で決めているか、向きが保存されるか/変更されるかをちゃんと追跡しないと混乱します。
向きの約束や保存/変更の法則は、様々な要因が絡んできて思いのほか複雑です。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\o}[1]{\overline{#1}}
\newcommand{\bs}[1]{\boldsymbol{#1}}
%\newcommand{\Imp}{ \Rightarrow }
\newcommand{\In}{ \text{ in } }
\newcommand{\op}{\mathrm{op}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Id}{\mathrm{Id}}
\newcommand{\Rev}{\mathrm{Rev}}
\newcommand{\hyp}{\text{-}}
%\newcommand{\hypp}{ \;\style{display: inline-block; transform: rotate(90deg)}{\|}\; }
%\newcommand{\twoto}{\Rightarrow}
\newcommand{\Iff}{\Leftrightarrow}
\newcommand{\For}{\text{For } }
%\newcommand{\Where}{\text{Where } }
%\newcommand{\BR}[1]{ \left[\!\left[ {#1} \right]\!\right] }
\newcommand{\dimU}[2]{{#1}\!\updownarrow^{#2}}
`$
内容:
高次圏とモノイド圏
高次圏とは言っても、扱うのは2次元までの圏です。2次元の圏は、0-射、1-射、2-射を持ちます。3-射は2-射のあいだの等式(あるいは恒等射)です。2次元の圏 $`\cat{K}`$ に対して、各次元の射の集合は次のように書きます。
- $`|\cat{K}|_0 := |\cat{K}| = \mrm{Obj}(\cat{K})`$
- $`|\cat{K}|_1 := \mrm{Mor}(\cat{K})`$
- $`|\cat{K}|_2 := \mrm{2Mor}(\cat{K})`$
$`A, B \in |\cat{K}|`$ に対して、$`\cat{K}(A, B)`$ はホム圏です。ホム圏の結合は縦結合と呼び、図式順結合記号 '$`;`$' で書きます。それとは別に、$`A, B, C\in |\cat{K}|`$ ごとの二項関手〈双関手〉として与えられる横結合があります。横結合の図式順結合記号は '$`*`$' とします。
$`\quad *_{A,B,C} : \cat{K}(A, B)\times \cat{K}(B, C) \to \cat{K}(A, C)`$
2次元の圏〈2-圏〉の定義は、「この2つのミニマムな解説はほんとに便利だ」で紹介したレンスターの"Basic bicat"にあります。ただし、味気ない定義だけです。また、2-圏に関わる呼び名や記法は人により違います(「高次圏: 用語法と文脈(主に2次元)」参照)。
$`\cat{M} = (\cat{M}, \otimes, I)`$ (記号の乱用)がモノイド圏のとき、$`\cat{M}`$ から2-圏 $`\cat{K}`$ を作れます。
- $`|\cat{K}|_0 := {\bf 1} = \{0\}`$
- $`|\cat{K}|_1 := |\cat{M}|`$
- $`|\cat{K}|_2 := \mrm{Mor}(\cat{M})`$
単元集合 $`{\bf 1}`$ の唯一の要素はなんでもいいですが、今日は気分で $`0`$ にしました。2-圏 $`\cat{K}`$ の対象はひとつしかないので、ホム圏もひとつです。そのホム圏はもとのモノイド圏の台圏だとします。
- $`\cat{K}(0, 0) := (\cat{M} \text{ as a plain category})`$
モノイド積 $`\otimes`$ を2-圏の横結合として使います。
$`\quad *_{0,0,0} := \otimes : \cat{K}(0, 0)\times \cat{K}(0, 0) \to \cat{K}(0, 0)`$
モノイド圏 $`\cat{M}`$ からこうして作られた2-圏を $`\cat{M}[1]`$ と書きます。$`[1]`$ のココロは、次元番号を1ずらす、ということです。
$`\quad |\cat{M}|_{k} = |\cat{M}[1]|_{k + 1}`$
モノイド圏の場合は、$`|\cat{M}|_{-1} = {\bf 1}`$ と考えます。
モノイド圏の定義は、「この2つのミニマムな解説はほんとに便利だ」で紹介したバエズの"Should know"にあります。
高次圏とモノイド圏の反対圏
「高次圏の反対圏をどう書くか」において、ブーム〈Gabriella Böhm〉の論文で使われている反対圏の記法を紹介しました。
ちょっと笑ってしまったのが、次の記法。
横方向の反転は下付きのopですが、縦方向の反転はopを90度回転して使ってます。
文字列の90度回転は面倒だし高次元化もできないので、通常の右肩 $`\op`$ に情報を追加します。追加情報は $`\{0, 1\}^2`$ で示します。
- $`(\hyp)^{\op(00)}`$ : 何もしない。実際には使わない。
- $`(\hyp)^{\op(10)}`$ : 1-射を反対にする。通常の $`(\hyp)^\op`$ と同じ。2-射はそのまま。
- $`(\hyp)^{\op(01)}`$ : 2-射を反対にする。1-射はそのまま。
- $`(\hyp)^{\op(11)}`$ : 1-射も2射も反対にする。
2-圏 $`\cat{K}`$ があるとき、2-射を捨てた1-圏を $`\dimU{\cat{K}}{1}`$ とします。この書き方については「圏の次元調整」を見てください。反対圏構成が、2-圏の切り捨て〈truncation〉とホム圏にどう影響するかは次のようです。$`A, B\in |\cat{K}|`$ とします。
$`\quad \dimU{\cat{K}^{\op(10)}}{1} = (\dimU{\cat{K}}{1})^\op \\
\quad \cat{K}^{\op(10)}(A, B) = \cat{K}(A, B)\\
\:\\
\quad \dimU{\cat{K}^{\op(01)}}{1} = {\dimU{\cat{K}}{1}} \\
\quad \cat{K}^{\op(01)}(A, B) = \cat{K}(A, B)^\op\\
\:\\
\quad \dimU{\cat{K}^{\op(11)}}{1} = (\dimU{\cat{K}}{1})^\op \\
\quad \cat{K}^{\op(11)}(A, B) = \cat{K}(A, B)^\op
`$
$`\cat{K}^{\op} = \cat{K}^{\op(10)}`$ ですが、1-射を反対にしても、個々のホム圏には何の影響もありませんから注意してください。
モノイド圏 $`\cat{M} = (\cat{M}, \otimes, I)`$ に対して、モノイド積の順番を反対にしたモノイド圏を作れます。
$`\quad \cat{M'} := (\cat{M}, \otimes', I)\\
\text{Where } A\otimes' B := B \otimes A
`$
こうして作ったモノイド圏 $`\cat{M'}`$ は $`\cat{M}^\mrm{co}`$ と書くのが習慣のようです。2-圏の反対圏との対応は次のようになります。
$`\quad \cat{M}^\mrm{co} \longleftrightarrow (\cat{M}[1])^{\op(10)}\\
\quad \cat{M}^\mrm{op} \longleftrightarrow (\cat{M}[1])^{\op(01)}\\
\quad \cat{M}^\mrm{coop} \longleftrightarrow (\cat{M}[1])^{\op(11)}
`$
モノイド圏は、単対象の2-圏として扱うと何かと便利です。
反変関手をそのまま扱う
「反対圏/反変関手と、2-圏のストリング図」において、我々が通常「反変関手」と呼んでいるものは、実際は共変関手であると言いました。
反変関手 $`F:\cat{C} \overset{-}{\to} \cat{D}`$ の代わりに、反対圏からの関手を使います。そして、代理である反対圏からの関手を「反変関手」と呼んでしまうのです。
小さい圏の2-圏 $`{\bf Cat}`$ や、大きい(小さいとは限らない)圏の2-圏 $`{\bf CAT}`$ のなかには、反変関手は存在しません。反変関手の代理となる共変関手が存在するだけです。通常は、これでも問題はないし、むしろ便利ですが、ときに“ほんとの反変関手”を考えたほうがいいこともあります。
関手 $`F:\cat{C} \to \cat{D}`$ を、ひとつの対象パート〈object part〉$`F_\mrm{obj}`$ とたくさんのホムパート〈hom part〉$`F_{\mrm{hom}(A, B)}`$ に分けます。記述を簡潔にするために:
- 対象パート $`F_\mrm{obj}`$ は、$`F_0`$ とも書く。
- ホムパート $`F_{\mrm{hom}(A, B)}`$ は、$`F_{(A, B)}`$ あるいは $`F_{A, B}`$ とも書く。
この記法で、ほんとの反変関手 $`G`$ を定義すると、素材となる写像達は:
- $`G_0 : |\cat{C}|_0 \to |\cat{D}|_0 \In {\bf SET}`$
- $`\For A, B\in |\cat{C}|\quad G_{A, B} : \cat{C}(A, B) \to \cat{D}(G_0(B), G_0(A)) \In {\bf Set}`$
ここでは、局所小圏〈locally small category〉だけを考えています。$`G_0(A), G_0(B)`$ の順番が入れ替わっているところが共変関手との違いです。反変関手が射の結合を保存する条件は次のように書けます。
$`\For f : A\to B, g:B \to C \In \cat{C}\\
\quad G_{A, C}(f;g) = G_{B, C}(g) ; G_{A, B}(f) \; : C \to A \In \cat{D}\\
\text{Where }\\
\quad G_{B, C}(g) \in \cat{D}(C, B),\; G_{A, B}(f) \in \cat{D}(B, A)
`$
「反対圏/反変関手と、2-圏のストリング図」でそうしたように、ほんとの反変関手を1-射として含む圏の2-圏を $`\o{\bf Cat}`$ 、$`\o{\bf CAT}`$ と書くことにします。また、共変・反変の別をプラス記号・マイナス記号で表します。プラス記号は省略可能です。
$`\quad F: \cat{C} \overset{+}{\to} \cat{D} \In \o{\bf CAT}\\
\quad G: \cat{C} \overset{-}{\to} \cat{D} \In \o{\bf CAT}
`$
ここから先、「反変関手」とは「ほんとの反変関手」のことです。反変関手の代理となる共変関手のことではありません。
反変関手を捨てて共変関手(符号プラス)だけを考えると部分2-圏となります。
$`\quad \o{\bf CAT}^{+} = {\bf CAT} \subseteq \o{\bf CAT}`$
しかし、共変関手を捨てて反変関手だけでは部分2-圏にはなりません。反変関手と反変関手の横結合が反変関手になるとは限らないので。それにも関わらず、反変関手(符号マイナス)だけを考えたホム圏は作れます。
$`\quad \o{\bf CAT}^{-}(A, B) \in |{\bf CAT}|`$
ホム圏の対象としての関手は、共変でも反変でもかまいません。対象の横結合は考えないので。ということは、対象の横結合(通常の関手の結合)を考えるケースでは具合が悪くなります。例えば、反変関手だけで自己関手のモノイド圏を作ることは(一般には)できません。
$`\quad \o{\bf CAT}^{-}(A, A) \not\in |{\bf MonCAT}|`$
関手圏の記号 $`[\cat{C}, \cat{D}]`$ の右肩にマイナス記号を付けて、反変関手を対象とする関手圏を表すことにします。
- $`[\cat{C}, \cat{D}]^{+} = [\cat{C}, \cat{D}]`$ : 通常の、共変関手を対象とする関手圏
- $`[\cat{C}, \cat{D}]^{-}`$ : 反変関手を対象とする関手圏
反対圏の対象と射
圏 $`\cat{C}`$ の反対圏 $`\cat{C}^\op`$ において、圏を構成している素材はもとの圏と同じです。
- $`|\cat{C}|_0 = |\cat{C}^\op|_0`$
- $`|\cat{C}|_1 = |\cat{C}^\op|_1`$
同じ集合でも、異なる構造の構成素なら区別したほうがいいだろう、と、「反対圏/反変関手と、2-圏のストリング図」で次のように書きました。
注釈情報を添える意味で次の記法を使ってもいいでしょう。
- $`\cat{C}^\op`$ の対象としての $`A\in \mrm{Obj}(\cat{C}) = \mrm{Obj}(\cat{C}^\op)`$ は $`A^\uparrow`$ と書く。
- $`\cat{C}^\op`$ の射としての $`f\in \mrm{Mor}(\cat{C}) = \mrm{Mor}(\cat{C}^\op)`$ は $`f^\uparrow`$ と書く。
上向き矢印は注釈情報なので、なくてもいいし、取り去っても何も変わりません。それでも、反対圏や反変関手につきまとう混乱を避ける効果はあります。
過去記事では、上向き矢印は「注釈情報」と書いてますが、ホムセットのあいだの写像ともみなせます。
$`\quad \cat{C}(A, B) \ni f \mapsto f^\uparrow \in \cat{C}^\op(B, A)`$
$`\cat{C}(A, B)`$ と $`\cat{C}^\op(B, A)`$ が集合として同じなのは確かですが、その集合の要素(射)には($`\mrm{dom}, \mrm{cod}`$ で与えられる)向きが付いていると考えるので、異なる向きの要素は異なるとも言えます。「同じとも言えるし、異なるとも言える」がややこしいところです。
ここでは、$`f:A \to B \In \cat{C}`$ と $`f^\uparrow : B \to A \In \cat{C}^\op`$ は、互いに対応するが異なるモノだとみなします。$`A\in |\cat{C}|`$ と $`A^\uparrow \in |\cat{C}^\op|`$ を区別するのは、あまり意味があるとは思えませんが、行きがかり上区別するのはかまわないでしょう。
ほんとの反変関手としての裏返し関手
「層化ストリング図 // 裏返し反変関手」において、裏返し関手〈reversing functor〉を導入しました。あまり強調しなかったのですが、裏返し関手はほんとの反変関手です。
$`\mrm{Rev} = \mrm{Rev}_\cat{C}`$ の対象パートとホムパートを書いてみると:
$`\mrm{Rev}_0 : |\cat{C}|_0 \to |\cat{C}^\op|_0 \In {\bf SET}\\
\For A \in |\cat{C}|_0\\
\quad \mrm{Rev}_0(A) = A \;\in |\cat{C}^\op|_0\\
\For A, B\in |\cat{C}|_0\\
\quad \mrm{Rev}_{A, B} : \cat{C}(A, B) \to \cat{C}^\op(\mrm{Rev}_0(B), \mrm{Rev}_0(A)) \In {\bf Set}\\
\quad \For f \in \cat{C}(A, B)\\
\qquad \mrm{Rev}_{A, B}(f) := f^\uparrow \;\in \cat{C}^\op(B, A)
`$
射の結合が反変に保存されることは:
$`\For f : A\to B, g:B \to C \In \cat{C}\\
\quad \mrm{Rev}_{A, C}(f;g) = \mrm{Rev}_{B, C}(g) ; \mrm{Rev}_{A, B}(f) \; : C \to A \In \cat{C}^\op\\
\text{Where }\\
\quad \mrm{Rev}_{B, C}(g) \in \cat{C}^\op(C, B),\; \mrm{Rev}_{A, B}(f) \in \cat{C}^\op(B, A)
`$
裏返し関手はほんとの反変関手なので、$`{\bf CAT}`$ のなかには居ません。つまり、通常お目にかかることはありません。
$`\quad \mrm{Rev}_\cat{C} : \cat{C} \overset{-}{\to} \cat{C}^\op \In \o{\bf CAT}^{-}`$
あるいは、
$`\quad \mrm{Rev}_\cat{C} \in |\o{\bf CAT}^{-}(\cat{C}, \cat{C}^\op)|`$
もっとも、反変関手の世界の住人が、共変関手の世界 $`\o{\bf CAT}^{+}(\cat{C}, \cat{C}^\op)`$ に絶対に現れないわけでもありません。例えば、可換モノイドを圏とみなした単対象小圏を $`\cat{A}`$ とすると、
$`\quad \cat{A}^\op = \cat{A}\\
\quad \mrm{Rev}_\cat{A} = \mrm{Id}_\cat{A} : \cat{A} \to \cat{A} \In {\bf Cat}
`$
反変でもあり共変でもあるヤツも少しいます。が、すべての裏返し関手を扱うには、反変関手も含む圏の2-圏 $`\o{\bf CAT}`$ で考える必要があります。
反変関手の共変化
反変関手を共変化するには、裏返し関手をプレ結合またはポスト結合します。この二種の共変化の操作を、2つの圏でインデックスされた関手の族として定義します。
- $`\bs{\Phi}_{\cat{C}, \cat{D}} : [\cat{C}, \cat{D}]^- \overset{+}{\to} [\cat{C}^\op, \cat{D}] \In \o{\bf CAT}`$
- $`\bs{\Psi}_{\cat{C}, \cat{D}} : [\cat{C}, \cat{D}]^- \overset{-}{\to} [\cat{C}, \cat{D}^\op] \In \o{\bf CAT}`$
以下、関手圏が局所小圏となる前提で考えます。$`\bs{\Phi}`$ の定義は:
$`\bs{\Phi} = \bs{\Phi}_{\cat{C}, \cat{D}} : [\cat{C}, \cat{D}]^- \overset{+}{\to} [\cat{C}^\op, \cat{D}] \In \o{\bf CAT}\\
%
\underline{\text{object part}}\\
\bs{\Phi}_0 : |[\cat{C}, \cat{D}]^-| {\to} |[\cat{C}^\op, \cat{D}]| \In {\bf SET}\\
\For G \in |[\cat{C}, \cat{D}]^-|\\
\quad \bs{\Phi}_0(G ) := \mrm{Rev}_{\cat{C}^\op} * G \;\in |[\cat{C}^\op, \cat{D}]|\\
%
\underline{\text{hom part} }\\
\For G, H \in |[\cat{C}, \cat{D}]^-|\\
\quad \bs{\Phi}_{G, H} : [\cat{C}, \cat{D}]^-(G, H) \to [\cat{C}^\op, \cat{D}](\bs{\Phi}_0(G), \bs{\Phi}_0(H) ) \In {\bf Set}\\
%
\quad \For \alpha \in [\cat{C}, \cat{D}]^-(G , H )\\
\qquad \bs{\Phi}_{G, H}(\alpha) := \mrm{Rev}_{\cat{C}^\op} * \alpha \; \in [\cat{C}^\op, \cat{D}](\mrm{Rev}_{\cat{C}^\op} * G , \mrm{Rev}_{\cat{C}^\op} * H)
`$
最後の行の $`*`$ は、2-圏 $`\o{\bf CAT}`$ における、関手と自然変換のヒゲ結合〈whiskering〉です。$`\bs{\Phi}_{G, H}`$ を省略なしで書くと、次のように4つのインデックスが付きます。
$`\quad (\bs{\Phi}_{\cat{C}, \cat{D}})_{G, H} : [\cat{C}, \cat{D}]^-(G, H) \to [\cat{C}^\op, \cat{D}](\bs{\Phi}_0(G), \bs{\Phi}_0(H) ) \In {\bf Set}`$
$`\bs{\Phi}`$ が共変関手であることは、次の形で結合が保存されることです。
$`\For \alpha : G\to H, \beta:H \to K \In [\cat{C}, \cat{D}]^-\\
\quad \bs{\Phi}_{G, K}(\alpha;\beta) = \bs{\Phi}_{G, H}(\alpha) ; \bs{\Phi}_{H, K}(\beta) \; : \mrm{Rev} * H \to \mrm{Rev}* K \In [\cat{C}^\op, \cat{D}]\\
\text{Where }\\
\quad \bs{\Phi}_{G, H}(\alpha) \in [\cat{C}^\op, \cat{D}] (G, H),\;
\bs{\Phi}_{H, K}(\beta) \in [\cat{C}^\op, \cat{D}](H, K)
`$
一方の $`\bs{\Psi}`$ は反変関手になります。$`\alpha : G \to H`$ が $`\bs{\Psi}(\alpha) : H \to G`$ に移ります。なぜかというと; 自然変換 $`\alpha`$ の成分は次の形です。
$`\quad \alpha_A : G(A) \to H(A) \In \cat{D}`$
各成分が $`G`$ から $`H`$ の方向に向いているので2-射〈自然変換〉も $`G \to H`$ の方向です。この成分達に裏返し関手 $`\mrm{Rev} = \mrm{Rev}_{\cat{D}}`$ を適用すると:
$`\quad \mrm{Rev}(\alpha_A) : \mrm{Rev}_0(H(A)) \to \mrm{Rev}_0(G(A)) \In \cat{D}^\op`$
裏返し関手は反変関手だったのでこうなります。対象パート $`\mrm{Rev}_0`$ は恒等だったので、
$`\quad \mrm{Rev}(\alpha_A) = {\alpha_A}^\uparrow : H(A) \to G(A) \In \cat{D}^\op`$
成分 $`\mrm{Rev}(\alpha_A)`$ 達は $`H`$ から $`G`$ の方向に向いているので、これらを成分に持つ自然変換の方向も $`H \to G`$ となります。成分 $`\mrm{Rev}(\alpha_A)`$ 達で形成される自然変換とは、ヒゲ結合 $`\alpha * \mrm{Rev}`$ です。
以上のことを踏まえて、$`\bs{\Psi}`$ の定義を書き出すと:
$`\bs{\Psi} = \bs{\Psi}_{\cat{C}, \cat{D}} : [\cat{C}, \cat{D}]^- \overset{-}{\to} [\cat{C}, \cat{D}^\op] \In \o{\bf CAT}\\
%
\underline{\text{object part}}\\
\bs{\Psi}_0 : |[\cat{C}, \cat{D}]^-| {\to} |[\cat{C}, \cat{D}^\op]| \In {\bf SET}\\
\For G \in |[\cat{C}, \cat{D}]^-|\\
\quad \bs{\Psi}_0(G ) := G* \mrm{Rev}_{\cat{D}} \;\in |[\cat{C}, \cat{D}^\op]|\\
%
\underline{\text{hom part} }\\
\For G, H \in |[\cat{C}, \cat{D}]^-|\\
\quad \bs{\Psi}_{G, H} : [\cat{C}, \cat{D}]^-(G, H) \to [\cat{C}, \cat{D}^\op]( \bs{\Psi}_0(H) , \bs{\Psi}_0(G)) \In {\bf Set}\\
%
\quad \For \alpha \in [\cat{C}, \cat{D}]^-(G , H )\\
\qquad \bs{\Psi}_{G, H}(\alpha) := \alpha * \mrm{Rev}_{\cat{D}} \; \in [\cat{C}, \cat{D}^\op](H * \mrm{Rev}_{\cat{D}}, G * \mrm{Rev}_{\cat{D}} )
`$
$`\bs{\Psi}`$ が反変関手であることは、次の形で結合が保存されることです。
$`\For \alpha : G\to H, \beta:H \to K \In [\cat{C}, \cat{D}]^-\\
\quad \bs{\Psi}_{G, K}(\alpha;\beta) = \bs{\Psi}_{H, K}(\beta) ; \bs{\Psi}_{G, H}(\alpha) ; \; : K * \mrm{Rev} \to G * \mrm{Rev} \In [\cat{C}, \cat{D}^\op]\\
\text{Where }\\
\quad \bs{\Psi}_{H, K}(\beta) \in [\cat{C}, \cat{D}^\op](K, H),\;
\bs{\Psi}_{G, H}(\alpha) \in [\cat{C}, \cat{D}^\op] (H, G)
`$
おわりに
ウーン、ややこしい、面倒くさい。しかも、これで話が終わりというわけではありません。「反対圏/反変関手と、2-圏のストリング図 // 反変関手」より:
扱いに困るのは $`{^\mrm{rev} F^{\mrm{rev}}}`$ です。内容的には $`F`$ とまったく同じですが、関手の域と余域は違うと言えば違うのです。「大域米田の補題」では、臨時に $`\widetilde{F}`$ という書き方をしてました。
共変関手を共変関手に移す変換 $`F \mapsto \widetilde{F}`$ もあります。通常、$`F`$ と $`\widetilde{F}`$ は同一視しますが、イズベル共役〈Isbell conjugacy〉や淡中双対性〈Tannaka duality〉を考えるときは、区別したほうが事情がハッキリします。
射の向きは、何次元の射であっても互いに反対になる二種類しかありません。二種類のどちらかにするか決めたり判断したりするだけのことです。なのに、ややこしい、面倒くさい。単純そうに見えても実は単純じゃない事はあるんですね。