すべての小さい2-圏(厳密2-圏とは限らない)達を対象とする3-圏 $`{\bf 2Cat}`$ があります。$`\mathcal{K}, \mathcal{L} \in |{\bf 2Cat}|`$ のとき、ホム2-圏 $`{\bf 2Cat}(\mathcal{K}, \mathcal{L})`$ が構成できます。ホム2-圏のk-射を(2, k)-変換手〈(2, k)-transfor〉と呼びます。ホム2-圏は変換手2-圏〈transfor 2-category〉とも呼べます。
ホム2-圏=変換手2-圏は、非常に豊かな構造を持ちます。そのため、定義や記述は複雑となり、近寄りがたい印象をいだきます。しかし、記法・図法を整理すれば、直感的にアクセス可能となります。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\pipe}{\mid }
%\newcommand{\msf}[1]{\mathsf{#1}}
\newcommand{\twoto}{\Rightarrow }
\newcommand{\In}{\text{ in } }
%\newcommand{\Imp}{ \Rightarrow }
%\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\hyp}{\text{-} }
\newcommand{\op}{\mathrm{op} }
%\newcommand{\id}{\mathrm{id} }
%\newcommand{\pto}{ \supseteq\!\to }
\newcommand{\u}[1]{\underline{#1}}
%\newcommand{\msc}[1]{\mathscr{#1}}
`$
内容:
はじめに
この記事を書き上げて読み直してみたら、“生の2-関手”と“生の2-自然変換”という言葉が気にかかりました。いくらなんでも唐突だろう、と。そこで、この記事を公開する前に次の記事を投稿しました。
その冒頭部分を引用すると:
一応書き終わってはいるのですがまだ投稿してないブログ記事があります。そのなかで、ちゃんと定義するのがめんどうなので雰囲気的な説明だけした上で、“生〈なま〉の2-関手”と“生〈なま〉の2-自然変換”という言葉を使っています。
「まだ投稿してないブログ記事」がこの記事です。“生の2-関手”と“生の2-自然変換”の問題は、先行した補足記事でだいたい解決したのではないかと思います。
「生の2-関手と生の2-自然変換」では、絵の描き方も少しだけ解説しています。ストライプ図を潰して(幅や広がりをゼロにして)ストリング図にする技法も紹介しています。昨日の記事とこの記事では、描き方が多少違うところもあります。以下はその例です。
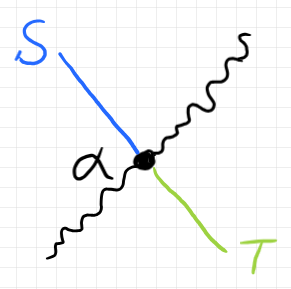
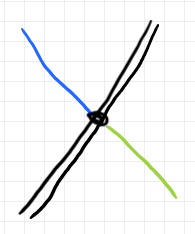
波線+ノードも二重線+ノードも、どちらも生の2-自然変換です。
この記事は最初に書いた時点からほとんど変更していません。そのため、後から追加した「生の2-関手と生の2-自然変換」との連携があまりとれてません。あしからず。
射と変換手
通常の圏〈1-圏〉は対象と射を持ちます。圏のあいだに関手があり、関手のあいだに自然変換があります。圏の次元が、2-圏、3-圏、‥‥ と上がっていくと、圏の構成素やそのあいだの対応付け、対応付けのあいだの対応付けなどに別々な個性的な名前を付けることは無理になってきます。番号〈次元〉で呼ぶことにします
| 従来の呼び名 | 番号による呼び名 |
|---|---|
| 圏の対象 | (1,0)-射 |
| 圏の射 | (1, 1)-射 |
| 圏の射のあいだの等式 | (1, 2)-射 |
| 関手 | (1, 0)-変換手 |
| 自然変換 | (1, 1)-変換手 |
| 自然変換のあいだの等式 | (1, 2)-変換手 |
番号による命名方式だと、2-圏の場合もスッキリと(あるいは味気なく)命名できます。
| 従来の呼び名 | 番号による呼び名 |
|---|---|
| 2-圏の対象 | (2, 0)-射 |
| 2-圏の射 | (2, 1)-射 |
| 2-圏の2-射 | (2, 2)-射 |
| 2-圏の2-射のあいだの等式 | (2, 3)-射 |
| 2-関手 | (2, 0)-変換手 |
| 2-自然変換 | (2, 1)-変換手 |
| 変更〈modification〉 | (2, 2)-変換手 |
| 変更のあいだの等式 | (2, 3)-変換手 |
一般に2-圏には(2, k)-射がありますが、特に(適当な $`\cat{K}, \cat{L}`$ に対する)ホム2-圏 $`{\bf 2Cat}(\cat{K}, \cat{L})`$ の(2, k)-射が(2, k)-変換手〈(2, k)-transfor〉です。同じことを別言すれば、(2, k)-変換手達で構成される2-圏がホム2-圏です。
ホム2-圏=変換手2-圏の構成素である変換手達を、次元だけで分類するのは大雑把過ぎます。変換手は代数的な特性を持っているからです。代数的特性も考慮すると、次の10種に分類するのがよいと思います。分類の方法はこの記事の最後に述べます。
- ラックス(2, 0)-変換手〈lax (2, 0)-transfor〉
- 反ラックス(2, 0)-変換手〈oplax (2, 0)-transfor〉
- 前方ラックス(2, 1)-変換手〈forward lax (2, 1)-transfor〉
- 前方反ラックス(2, 1)-変換手〈forward oplax (2, 1)-transfor〉
- 後方ラックス(2, 1)-変換手〈backward lax (2, 1)-transfor〉
- 後方反ラックス(2, 1)-変換手〈backward oplax (2, 1)-transfor〉
- 前方ラックス(2, 2)-変換手〈forward lax (2, 1)-transfor〉
- 前方反ラックス(2, 2)-変換手〈forward oplax (2, 1)-transfor〉
- 後方ラックス(2, 2)-変換手〈backward lax (2, 2)-transfor〉
- 後方反ラックス(2, 2)-変換手〈backward oplax (2, 2)-transfor〉
反ラックス〈oplax〉は余ラックス〈colax | コラックス〉ともいいます。「ラックスかつ反ラックス」の意味の形容詞はタイト〈tight〉を使います。多くの場合、「タイト」を「強」〈strong〉といいますが、用語のコンフリクト〈かち合い〉が起きてとてもイヤなので、僕は「強」を使いません。
この記事で説明するのは、次の(2, k)-変換手です。その他は「以下同様」で大丈夫だと思いますので。
- ラックス(2, 0)-変換手〈lax (2, 0)-transfor〉
- 前方ラックス(2, 1)-変換手〈forward lax (2, 1)-transfor〉
- 前方ラックス(2, 2)-変換手〈forward lax (2, 2)-transfor〉
使用する名前・文字・記号
$`\cat{K}, \cat{L}\in |{\bf 2Cat}|`$ とします。単に (2-k)-射といった場合、選ばれた2-圏 $`\cat{K}, \cat{L}`$ の(2, k)-射のことだとします。(2, k)-変換手は、ホム2-圏 $`{\bf 2Cat}(\cat{K}, \cat{L})`$ の(2, k)-射のことです。ホム2-圏に属する射は、必ず「変換手」と呼びます(ここでのお約束)。
(2, k)-変換手は、単なる写像のようなものではなくて、それ自体が代数構造を持ちます。
- ラックス(2, 0)-変換手は、モノイドと類似している。
- 前方ラックス(2, 1)-変換手は、2つのモノイドが左斜め作用する斜め加群(後述)と類似している。
- 前方ラックス(2, 2)-変換手は、2つのモノイドが左斜め作用する斜め加群のあいだの準同型射と類似している。
以上の類似性を強調して、次の呼び名も使います。
- ラックス(2, 0)-変換手を、変換手的モノイド〈transforial monoid〉とも呼ぶ。
- 前方ラックス(2, 1)-変換手を、変換手的左斜め加群〈transforial left oblique module〉とも呼ぶ。
- 前方ラックス(2, 2)-変換手を、変換手的左斜め加群射〈transforial left oblique module morphism〉とも呼ぶ。
したがって、上記3種類の(2, k)-変換手で構成される2-圏は次のように記述できます。
- 変換手的モノイドを0-射〈対象〉として、変換手的左斜め加群を1-射として、変換手的左斜め加群射を2-射とする2-圏
変換手2-圏を理解するための1つ目のポイントは、この代数構造に着目することです。上記の変換手2-圏は、次のような代数構造の2-圏と類似しているのです。
- モノイドを0-射〈対象〉として、左斜め加群を1-射として、左斜め加群射を2-射とする2-圏
2-圏のk-射と、ホム2-圏のk-射〈(2, k)-変換手〉を見てすぐ区別できるように、(2, k)-射と(2, k)-変換手を表す変数名〈文字〉の種別を約束しておきましょう。まず原則として:
- 2-圏内の(2, k)-射は小文字で表す。
- ホム2-圏内の(2, k)-変換手は大文字で表す。
次元 k ごとの文字種別は:
- (2, 0)-射は、ラテン小文字 $`a, b`$ などで表す。
- (2, 1)-射は、ラテン小文字 $`f, g`$ などで表す。
- (2, 2)-射は、ギリシャ小文字 $`\varphi, \psi`$ などで表す。
- (2, 0)-変換手は、ラテン大文字 $`A, B`$ などで表す。
- (2, 1)-変換手は、ラテン大文字 $`F, G`$ などで表す。
- (2, 2)-変換手は、ギリシャ大文字 $`\Phi, \Psi`$ などで表す。
多くの人が違和感をいだくのは、(2, 0)-変換手と(2, 1)-変換手でしょう。
- ラテン大文字 $`A, B`$ は、(2, 0)-変換手ではなくて(2, 0)-射〈対象〉のように思える。
- ラテン大文字 $`F, G`$ は、(2, 1)-変換手ではなくて(2, 0)-変換手〈2-関手〉のように思える。
まー、それはそうでしょう。が、違和感は単に“気分”の問題です。上記のような一律なルールを決めてそれに従えば、煩雑さや混乱を避けられます。
変換手2-圏を理解するための2つ目のポイントは、一律なルールを決めて従うことです。一律なルールが今述べたルールと違ってもかまいませんが、出来るだけ単純で例外のないルールにします。
2-圏(ここでは $`\cat{K}, \cat{L}`$)と、変換手2-圏($`{\bf 2Cat}(\cat{K}, \cat{L})`$)における演算子記号も決めておきます。
- (2, 1)-射どうし、または(2, 2)-射どうし、または(2, 1)-射と(2, 2)-射の横結合は、図式順二項演算子記号 '$`\ast`$'(アスタリスク)を使う。
- (2, 2)-射どうしの縦結合は、図式順二項演算子記号 '$`;`$'(セミコロン)を使う。
- (2, 1)-変換手どうし、または(2, 1)-変換手どうし、または(2, 2)-変換手と(2, 2)-変換手の横結合は、図式順二項演算子記号 '$`\star`$'(黒星印)を使う。
- (2, 2)-変換手どうしの縦結合は、図式順二項演算子記号 '$`\pipe`$'(パイプ記号)を使う。
(2, k)-射のプロファイル(域と余域の仕様)は次のように書きます。
$`\quad a \In \cat{K} \text{ または } a \in |\cat{K}|\\
\quad f:a \to b \In \cat{K} \text{ または } f \in |\cat{K}(a, b)|\\
\quad \varphi :: f\twoto g :a \to b \In \cat{K} \text{ または } \varphi \in \cat{K}(a, b)(f, g)
`$
(2, k)-変換手のプロファイルは次のように書きます。
$`\quad A: \cat{K} \to \cat{L} \In {\bf 2Cat}\\
\quad \text{ または } A \In {\bf 2Cat}(\cat{K}, \cat{L}) \text{ または } A \in |{\bf 2Cat}(\cat{K}, \cat{L})|\\
\quad F:: A \twoto B : \cat{K} \to \cat{L} \In {\bf 2Cat}\\
\quad \text{ または } F:A \to B \In {\bf 2Cat}(\cat{K}, \cat{L}) \\
\quad \text{ または } F \in |{\bf 2Cat}(\cat{K}, \cat{L})(A, B)|\\
\quad \Phi ::: F \Rrightarrow G :: A \twoto B : \cat{K} \to \cat{L} \In {\bf 2Cat}\\
\quad \text{ または } \Phi :: F \twoto G :A \to B \In {\bf 2Cat}(\cat{K}, \cat{L}) \\
\quad \text{ または } \Phi \in {\bf 2Cat}(\cat{K}, \cat{L})(A, B)(F, G)
`$
と、色々と書き方の約束を決めましたが、この記事内ではあまり約束を使わなかったですね。ラベルがない絵で表しているからです。絵からテキストへの翻訳をするときは、書き方の約束は必須です。約束ごとを決めることで概念の整理にもなります。
変換手の構成素達
ひとつの(2, k)-変換手は、多くの構成素から成り立ちます。それらの構成素を正確にしかし効率的に記述する必要があります。このときの指針(変換手2-圏を理解するための3つ目のポイントですが)は、記号の乱用をほどよく使い、使いすぎないことです。
とはいえ、記号の乱用の“良いあんばい”とはどのようなものでしょう。既に使っている事例から学ぶことにします。1つ目のポイントを思い出すと、「代数構造に着目する」でした。その代数構造は、モノイド/加群/加群射に類似しているのでした。よって、モノイド/加群/加群射に関する“良いあんばい”の記号の乱用を真似すればよいことになります。
いま(一時的に)、$`A`$ をモノイドとしましょう。モノイドは、台集合に乗法〈二項演算〉と単位が載ったものですから、次のように書くべきでしょう。
$`\quad A = (\u{A}, m^A, e^A)`$
ここで、$`\u{A}`$ はモノイド $`A`$ の台集合〈underlying set〉です。$`m^A`$ はモノイド $`A`$ の乗法、$`e^A`$ はモノイド $`A`$ の単位です。モノイドと呼んだ時点で、結合律と左単位律/右単位律は仮定します。
モノイド $`A`$ を簡潔に書きたいなら、次のような記号の乱用は許されるでしょう。
$`\quad A = (A, m, e)`$
さて、(また一時的に)$`F`$ をモノイド $`A`$ が左から作用する加群としましょう。$`A`$-左加群は、台集合に(モノイドの)左作用が載ったものですから、次のように書くべきでしょう。
$`\quad F = (\u{F}, l^F)`$
ここで、$`\u{F}`$ は$`A`$-左加群 $`F`$ の台集合です。$`l^F`$ はモノイド $`A`$ による左作用です。左加群と呼んだ時点で、左作用の結合律と単位律は仮定します。
$`A`$-左加群 $`F`$ を簡潔に書きたいなら、次のような記号の乱用は許されるでしょう。
$`\quad F = (F, l)`$
(また一時的に)$`\Phi`$ を$`A`$-左加群 $`F`$ から $`G`$ への左加群射としましょう。$`\Phi`$ は台集合のあいだの写像ですから、次のように書けます。
$`\quad \Phi : \u{F} \to \u{G}`$
左加群射と呼んだ時点で、左作用が保存されることは仮定します。
左加群とその台集合をオーバロードする記号の乱用を使っているなら、$`\Phi`$ を次のように書くことも許されるでしょう。
$`\quad \Phi : F \to G`$
以上に述べたほどよい記号の乱用を、(2, k)-変換手に対しても適用します。
今度は、$`A`$ を変換手的モノイド=ラックス(2, 0)-変換手とします。変換手的モノイドは、台〈underlying thing〉に乗法と単位が載ったものなので、次のように書きます。
$`\quad A = (\u{A}, \nu^A, \iota^A) \\
\quad A = (A, \nu, \iota) \:(\text{記号の乱用})
`$
台 $`\u{A}`$ は“生の2-関手”〈raw 2-functor〉です。$`\nu^A`$ はラックス2-関手 $`A`$ の乗法ラクセイター*1、$`\iota^A`$ はラックス2-関手 $`A`$ の単位ラクセイターです。変換手的モノイドと呼んだ時点で、結合律と左単位律/右単位律は仮定します。“生の2-関手”とは何であるか? ラクセイターとは何であるか? 結合律/左単位律/右単位律とは何であるか? は、次節以降で述べます。
次に、$`F`$ を変換手的モノイド $`A`$ から変換手的モノイド $`B`$ への変換手的左斜め加群とします。$`(A, B)`$-変換手的左斜め加群は、台に(変換手的モノイドから変換手的モノイドへの)変換手的左斜め作用が載ったものですから、次のように書きます。
$`\quad F = (\u{F}, \lambda^F) \\
\quad F = (F, \lambda) \:(\text{記号の乱用})
`$
$`F = (\u{F},\lambda^F)`$ の実体は“生の2-自然変換”(raw 2-natural transformation)です。$`\lambda^F`$ は変換手的モノイド $`A`$ から変換手的的モノイド $`B`$ への変換手的左斜め作用です。変換手的左斜め加群と呼んだ時点で、変換手的左斜め作用の左斜め結合律と左斜め単位律は仮定します。“生の2-自然変換”とは何であるか? 変換手的左斜め加群/変換手的左斜め作用とは何であるか? 左斜め結合律/左斜め単位律とは何であるか? は、次節以降で述べます。
$`\Phi`$ を$`(A, B)`$-変換手的左斜め加群 $`F`$ から $`G`$ への変換手的左斜め加群射とします。$`\Phi`$ は台のあいだの準同型射ですから、次のように書きます。次元の都合で二重矢印を使います。
$`\quad \Phi :: \u{F} \twoto \u{G}\\
\quad \Phi :: F \twoto G \:(\text{記号の乱用})
`$
変換手的左斜め加群射と呼んだ時点で、変換手的左斜め作用が保存されることは仮定します。台のあいだの準同型射とは何であるか? 変換手的左斜め作用が保存されるとは何であるか? は次節以降で述べます。
変換手的モノイドと描画法
変換手2-圏を理解するための4つ目のポイントは、ストリング図/ストライプ図を活用することです。ストリング図/ストライプ図を活用することにより、(2, k)-変換手そのものと(2, k)-変換手が満たすべき法則の記述が劇的に簡単かつ直感的になります。しかし、ストリング図/ストライプ図に慣れている人があまりいないので、現実的には一番難しいポイントかも知れません。
(2, k)-変換手の説明と並行して、それを描くためのストリング図/ストライプ図の説明をするのが望ましいでしょうが、それをやると長大な記事になってしまうので、ストリング図/ストライプ図の説明はしません。ブログ内検索を手がかりに、過去記事の説明を探してみてください。(「生の2-関手と生の2-自然変換」に少し描画法の説明があります。)
2-圏 $`{\bf 2Cat}(\cat{K}, \cat{L})`$ 内の変換手的モノイド $`A`$ を描くときは次のようにします。
- $`A`$ の台 $`\u{A}`$ は、ワイヤー〈ストリング〉で描く。ワイヤーは生の2-関手です。
- $`A`$ の乗法ラクセイター $`\nu^A`$ は、黒丸〈ドット | まるいボックス〉で描く。黒丸は生の2-自然変換です。
- $`A`$ の単位ラクセイター $`\iota^A`$ は黒三角〈上にとがったボックス〉で描く。黒三角は特殊な生の2-自然変換です。
ワイヤーとボックス(黒丸、黒三角のボックス)の内部構造を描くときはストライプ図を使います。ストライプの内部には $`\cat{K}`$ の様子を、ストライプの外部(キャンバスの地の部分)には $`\cat{L}`$ の様子を描きます。ストリング図の絵図要素〈pictorial element〉達と、その内部構造を描いたストライプ図達は次のようです。
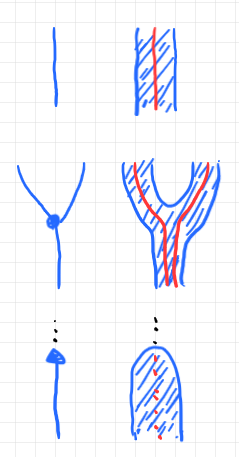
キャンバスの描画方向は、縦結合の方向が上から下、横結合の方向が左から右です。僕は、この描画方向が一番自然だと思っています。
上から順に、$`A`$ の台 $`\u{A}`$ 、$`A`$ の乗法ラクセイター $`\nu^A`$ 、$`A`$ の単位ラクセイター $`\iota^A`$ です。赤いワイヤーは $`\cat{K}`$ の射〈1-射〉です。赤い点線は $`\cat{K}`$ の単位射(横結合の恒等)で、黒い点線は $`\cat{L}`$ の単位射です。ストライプの内部のエリアが $`\cat{K}`$ の対象〈0-射〉、ストライプの外部のエリアが $`\cat{L}`$ の対象〈0-射〉を表します。
(2, k)-変換手に関する法則は、だいたいストリング図で描けますが、ストライプ図で内部構造を描かないと表せない法則もあります。例えば次の図がそうです。
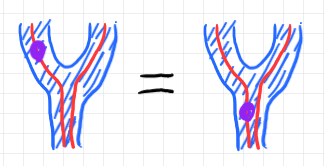
紫のオダンゴが $`\cat{K}`$ の2-射で、それが、$`A`$ の乗法ラクセイターを通過して下にスライドしています。このような法則は、幅(面積)を持たないワイヤーだけではうまく描けません
変換手的モノイド〈ラックス(2, 0)-変換手〉は、モノイドと同様に結合律と左単位律/右単位律を満たします。それらの法則は次のように描けます。
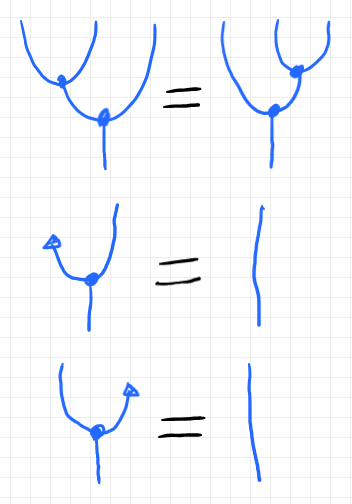
青いワイヤー、またはそれに幅を付けたストライプが表すものは“生の2-関手” $`\u{A}`$ です。$`\u{A}`$ は、2-圏 $`\cat{K}`$ の0-射/1-射/2-射をそれぞれ、$`\cat{L}`$ の0-射/1-射/2-射へと移す写像で、k-射のあいだの(図形的な)境界関係を(等式的に)保ち、2-射の縦結合も(等式的に)保つものです。
ストリング図の黒丸や黒三角(いや、ブルーの丸や三角だ)のボックス〈ノード〉は、“生の2-自然変換” です。“生の2-自然変換”は(“生の2-関手”も)「生の2-関手と生の2-自然変換」に説明があります。
これらの絵が表すことを、テキストとして書き下すには、すべてのエリア、ワイヤー〈ストリング〉、ボックス(黒丸と黒三角)、さらにストライプで内部構造を描いた場合の内部エリア、内部ワイヤーに対して名前を付けて、様々な記号と組み合わせて、等式または可換図式に翻訳する必要があります。今日はその翻訳作業については述べません。面倒くさくていつもウンザリするのですが、いつかそこもシッカリやらないとなー、とは思っています。
変換手的左斜め加群と描画法
「斜め加群」という言葉は過去に何度か使っています。
初出の説明は次の過去記事ですね。
通常、モノイドが左から作用する左加群というと、モノイド作用が“右側”に影響することはないのですが、左斜め加群では、左モノイド作用は加群の台と共に右に居るモノイドにも影響します。このような(って、どのようだ?)左斜め加群の概念を、“生の2-関手”のワイヤーと“生の2-自然変換”のボックスで描くと、変換手的左斜め加群〈前方ラックス(2, 1)-変換手〉になります。
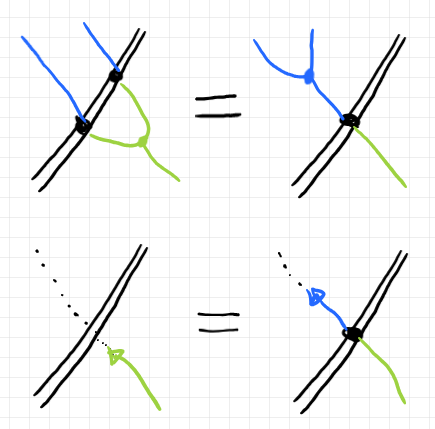
次の図が、変換手的モノイド $`A`$ から変換手的モノイド $`B`$ への変換手的左斜め加群 $`F`$ を表します。

- 青いワイヤーは、変換手的モノイド $`A`$ の台 $`\u{A}`$ 。
- 緑のワイヤーは、変換手的モノイド $`B`$ の台 $`\u{B}`$ 。
- 黒二重線のワイヤーは、変換手的左斜め加群 $`F`$ の台 $`\u{F}`$ 。
- 黒二重線上の黒丸は、変換手的左斜め加群 $`F`$ の左斜め作用 $`\lambda^F`$ 。
変換手的左斜め加群の左斜め作用 $`\lambda^F`$ が満たすべき法則〈公理〉は、$`A`$ の乗法・単位、$`B`$ の乗法・単位と整合することです。絵で見ると、モノイド乗法ボックス(青と緑のマル)とモノイド単位ボックス(青と緑の三角)が、左斜め加群の台(二重線)を通り抜けることができます。
変換手的左斜め加群射と描画法
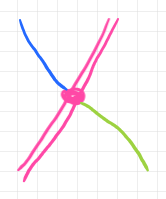
前節の変換手的左斜め加群 $`F`$ と、もうひとつ変換手的左斜め加群 $`G`$ があるとします。どちらも、変換手的モノイド $`A`$ から $`B`$ へ向かう変換手的左斜め加群です。$`G`$ は次の図で表すことにします。
変換手的左斜め加群 $`F`$ から $`G`$ への変換手的左斜め加群射〈前方ラックス(2, 2)-変換手〉 $`\Phi`$ とは、$`F`$ の台 $`\u{F}`$(黒の二重線)から $`G`$ の台 $`\u{G}`$(ピンクの二重線)へのボックス(白抜きのマル、“生の2-自然変換”の変種)です。以下がそうです。
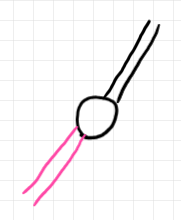
$`\Phi :: \u{F} \twoto \u{G}`$ が満たすべき法則はひとつだけです。それは、$`\Phi`$ が、変換手的左斜め加群の左斜め作用を保つことです。絵で見ると、$`F`$ の左斜め作用を $`\Phi`$ を通り抜けてスライドして、$`G`$ の左斜め作用まで移動することができます。
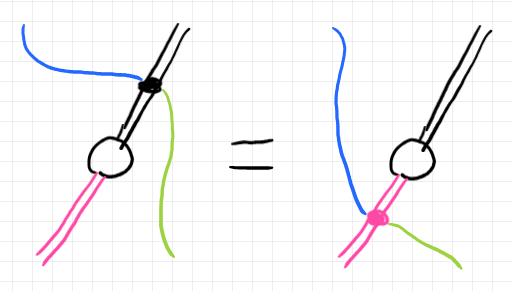
(2, k)-変換手の分類
ラックス(2, 0)-変換手は、変換手的モノイドでした。反ラックス(2, 0)-変換手は、変換手的コモノイドになります。モノイド演算とモノイド法則をすべて逆向きにすると、コモノイド演算とコモノイド法則になります。この記事の描画法なら、上下をひっくり返します。
前方ラックス(2, 1)-変換手は、変換手的左斜め加群でした。「左」はこの記事の描画法において、左作用になるからです。描画方向を変えると「左右」は変わってしまいます。それで、形容詞「前方」を使いました。この記事の描画法において右作用にすると、後方ラックス(2, 1)-変換手になります。モノイドの代わりにコモノイド余作用を考えると、前方反ラックス(2, 1)-変換手と後方反ラックス(2, 1)-変換手が出てきます。
(2, 2)-変換手の分類は、どのような(2, 1)-変換手のあいだの斜め加群射であるかのよって分類しています。よって、(2, 1)-変換手と同じだけの種類があります。
おわりに
ストリング図/ストライプ図を使うと、(2, k)-変換手とその法則の記述が簡単に直感的に行なえます。しかし、絵の描き方を知らない人から見ると、「それは何なの? 何を描いているの? 何を意味しているの?」となり、結局意味不明です。
「「コミュニケーションの多次元化」という革命に立ち会っているのだと思う」に書いたように、2次元以上の空間次元を駆使する絵図言語〈{pictorial | graphical | diagrammatic} language〉が、30年、50年あるいは100年のスパンでは台頭すると思いますが、現状では、絵の描き方を学ぶのも伝えるのも極めてコストリーで、なかなかうまくいきません(ため息)。
*1:乗法ラクセイターを compositor と呼ぶこともあります。可逆なラクセイターを strongator と呼んでいる例もあります。