バエズ/ドーラン・ツリー〈Baez-Dolan tree〉は、オフィシャルには組み合わせ的構造です、視覚化のために3次元または2次元の空間のなかに描き出し〈レンダリングし〉ます。3次元空間内に、幹や枝がパイプになっているツリーとして描くことが標準的描画法です*1。が、標準表示には問題点があります。
- 描くのに手間がかかり過ぎる。
- 情報の一部が隠れて見えなくなってしまう。
この欠点を補う描画法が円板表示と要約ツリーです。
バエズ/ドーラン・ツリーの要約ツリーは、要約の仕方によって色々と変わります。要約の仕方は、ツリーの分解の仕方、あるいは合成の仕方に対応します。分解・合成の仕方を端的に描いたツリーがシームツリーです。
この記事では、次の描画法を紹介します。
- バエズ/ドーラン・ツリーの標準表示(3次元空間内に)
- バエズ/ドーラン・ツリーの円板表示(2次元平面内に)
- バエズ/ドーラン・ツリーの要約ツリー
- シーム付きバエズ/ドーラン・ツリーのシームツリー
また、穴、シーム、スポットという概念についても述べます。
内容:
標準表示と円板表示
「穴」という言葉が大変に紛らわしいので、「バエズ/ドーラン植物 // 曲面の穴ってなに?」を参照して、「穴」の用法を確認してください。本記事では、種数〈genus〉を決定する穴ではないほうの穴を、紛らわしい場合は「穴〈空洞〉」と書くことにします。
まずは、バエズ/ドーラン・ツリーを標準表示〈standard presentation〉した例を挙げます。
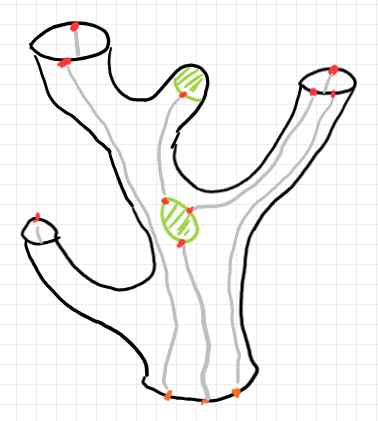
バエズ/ドーラン・ツリーは、通常の3次元空間($`{\bf R}^3`$)内に描かれており、現実世界の木と同じように下側に根〈ルート〉があり上に向かって枝葉が繁るとします。幹や枝は中空のパイプです。ツリーのルート〈根〉とリーフ〈葉〉の部分は穴〈空洞〉があいています。バエズ/ドーラン・ツリーの形状は穴〈空洞〉があいた曲面です。
曲面の境界は幾つかの円周で、それぞれを境界円周〈boundary circle〉、または単に円周〈circle〉と呼びます。ルートの位置の円周はルート円周〈root circle〉、リーフの位置の円周はリーフ円周〈leaf circle〉です。穴〈空洞〉には実体がありませんが、穴〈空洞〉と一対一対応する境界円周は図形的な実体(3次元空間内の円周)を持ちます。したがって、穴〈hole〉は境界円周の同義語だと解釈します。
境界円周上の赤い点はポート点〈port point〉または単にポート〈port〉と呼びます。ポートとポートはワイヤー〈wire〉(絵ではグレーの線)で結ばれます。同一ポートに戻るワイヤーは認めません(ワイヤーは異なる2つのポートを結ぶ)。どのポートにも接続しない例外ループ〈exceptional loop〉(「バエズ/ドーラン植物 // 例外ループ」参照)となるワイヤーを認める場合もあります。
ポートには色(と呼ばれる値)が付きますが、この記事では色については言及しません。ワイヤーには向きが付く場合と向き無しの場合があります。この記事では、ワイヤーには向きがないとします。向き無しの例外ループはあるかも知れません。
緑に塗ってある小さな領域はスポット〈spot〉と呼びます。スポットは穴〈空洞〉ではありません。スポットの縁〈ふち〉も円周の形はしていてポートが載っています。しかし、スポットの縁を境界円周とは呼びません。曲面の境界〈boundary〉ではないからです。スポットの縁はボーダーとは呼べます(ボーダーの定義は後述)。スポットについては後で詳しく述べます。
3次元空間内のバエズ/ドーラン・ツリーは、ルート円周を広げて上から押しつぶすことにより、2次元平面内の穴あき円板として描けます。それがバエズ/ドーラン・ツリーの円板表示〈{disc | disk } presentation〉で、以下のようになります。
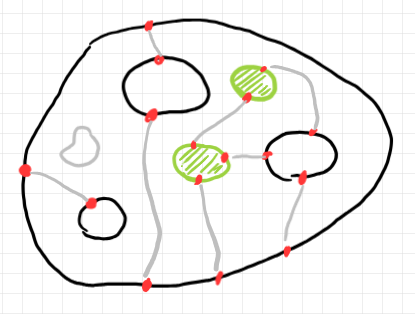
円板表示は、標準表示に比べて描画の手間がかかりません。また、すべての情報を描けます。ポートの個数とワイヤーの本数を勘定してみましょう。
| ポートの個数 | ワイヤーの本数 | |
|---|---|---|
| 標準表示 | 13個 | 8本(3本は接続先不明) |
| 円板表示 | 16個 | 9本(例外ループ含む) |
標準表示では隠れていたポート/ワイヤーがあったわけです。
要約ツリーとシームツリー
バエズ/ドーラン・ツリーの概要を簡単な形状のツリーとして表しましょう。以下で、$`A`$ と呼ばれるバエズ/ドーラン・ツリー(の標準表示)とその要約ツリー〈summary tree〉、円板表示を示します。
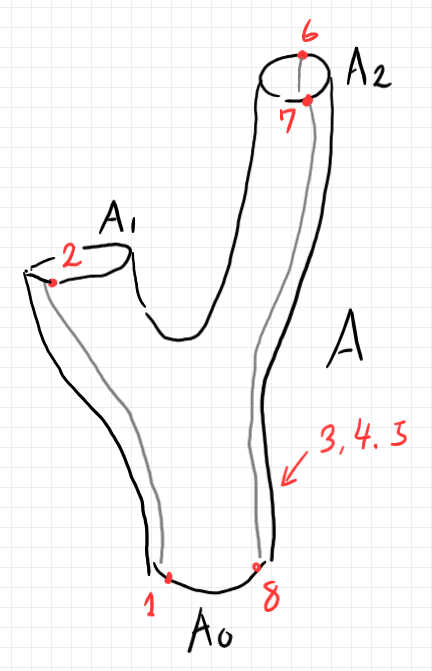
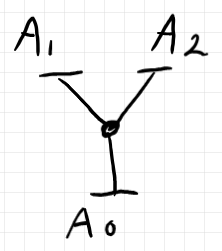
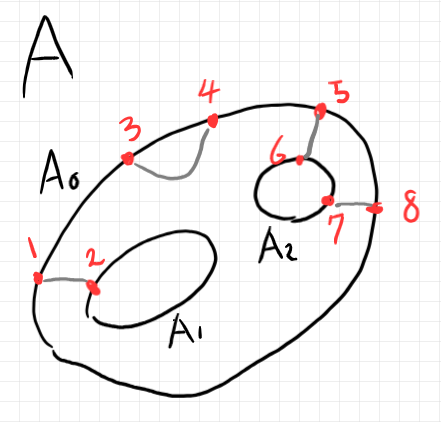
要約ツリーに描かれるのは次の情報だけです。
- 境界円周を横棒で描く。ルート円周が下の横棒。リーフ円周が上の二本の横棒。
- 黒丸はワイヤリングを象徴的に表す。黒丸からは何の情報も読み取れない。
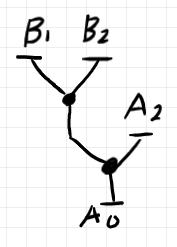
以下は、$`B`$ と呼ばれるバエズ/ドーラン・ツリー(の標準表示)とその要約ツリー、円板表示です。ポート番号が (2) と書いてあるのは、後で $`A`$ の2番ポートと接続する心づもりがあるからです。
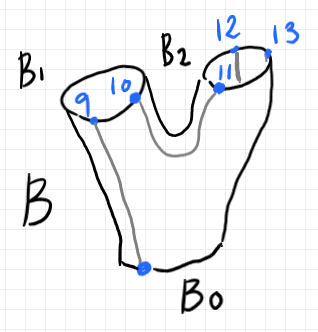
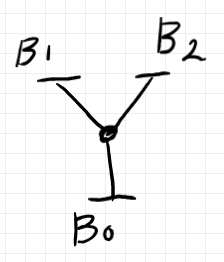
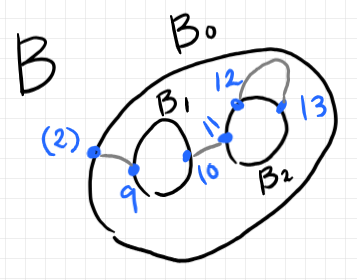
以上の2つのバエズ/ドーラン・ツリー $`A`$ と $`B`$ を繋ぎます。円周 $`B_0`$ と円周 $`A_1`$ が重なるようにして、赤い2番ポートと青の2番ポートが一致するようにします。
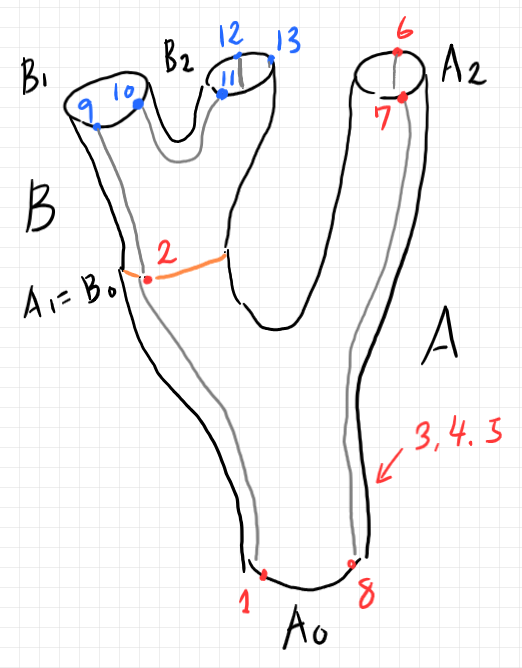
オレンジで描いている繋ぎ目をシーム〈seam | 縫い目〉と呼びます。シームは、図形としては円周でポートを載せています。シームが描かれた状態のバエズ/ドーラン・ツリーをシーム付きバエズ/ドーラン・ツリー〈seamed Baez-Dolan tree〉、あるいは単にシーム付きツリー〈seamed tree〉と呼びます。
シーム付きツリーの要約ツリーは以下のように描きます。シームはオレンジ色のエッジです。
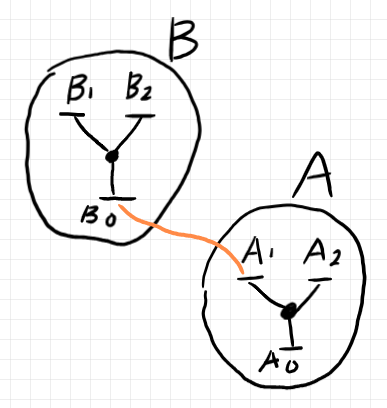
シームがエッジとして描かれたツリーをシームツリー〈seam tree〉と呼びます。上の例では、要約ツリーも描いていますが、要約ツリーも省略してシームだけを描くと下のようになります。
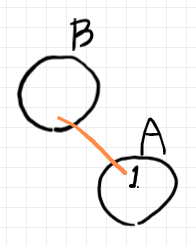
これから分かることは、$`B`$ というバエズ/ドーラン・ツリーのルート円周が、$`A`$ というバエズ/ドーラン・ツリーの1番のリーフ円周と重なるということだけです。シームは、接ぎ木〈grafting〉とか溶接〈welding〉とか裁縫〈sewing〉と呼ばれる演算(総称的・一般的にオペラッド結合〈operadic composition〉)の様子だけを知りたいときは有効です。何段階かのシームがあるときは、シームツリーにより接ぎ木/溶接/裁縫の様子がわかります(下図)。
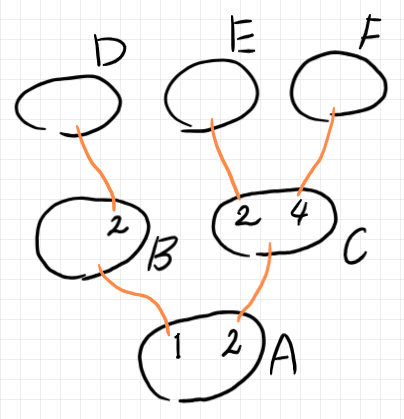
シーム付きバエズ/ドーラン・ツリー
シーム付きバエズ/ドーラン・ツリーは、複数のバエズ/ドーラン・ツリーの繋ぎ合わせ方の情報を一本のバエズ/ドーラン・ツリーのなかに描き込んだものです。
次の絵は、スピヴァックの論文 [Spi13] からの画像コピーです。
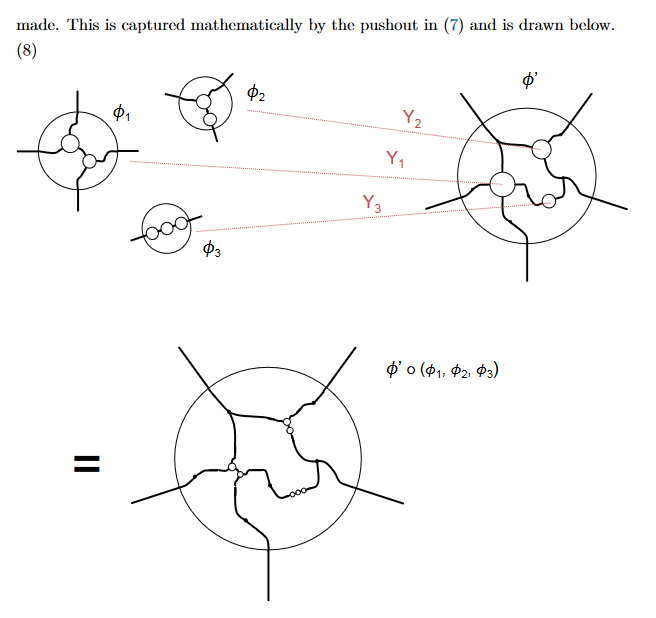
- [Spi13]
- Title: The operad of wiring diagrams: formalizing a graphical language for databases, recursion, and plug-and-play circuits
- Author: David I. Spivak
- Submitted: 1 May 2013
- Pages: 28p
- URL: https://arxiv.org/abs/1305.0297
$`\phi_1, \phi_2, \phi_3, \phi'`$ はバエズ/ドーラン・ツリー(の円板表示)だと思ってかまいません。$`\phi'`$ の3つの穴に、$`\phi_1, \phi_2, \phi_3`$ をはめ込んで新しいバエズ/ドーラン・ツリーを作り出している絵です。この絵のなかの $`Y_1, Y_2, Y_3`$ がはめ込み方を指示する写像ですが、これらの写像はシームと同じことです。
ポートとワイヤーは無視して、スピヴァックの $`Y_1, Y_2, Y_3`$ を含む絵を、シーム付きバエズ/ドーラン・ツリー(の標準表示)として描くと次のようになります。
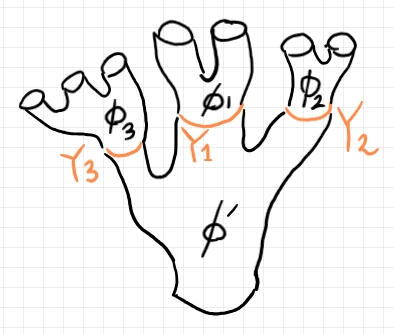
スピヴァックの絵の等式の右辺($`\phi'\circ (\phi_1, \phi_2, \phi_3)`$)では、シーム(繋ぎ目)の情報は消えています。そのことを表すと次のようになります。波線矢印は、シームを消す操作です。
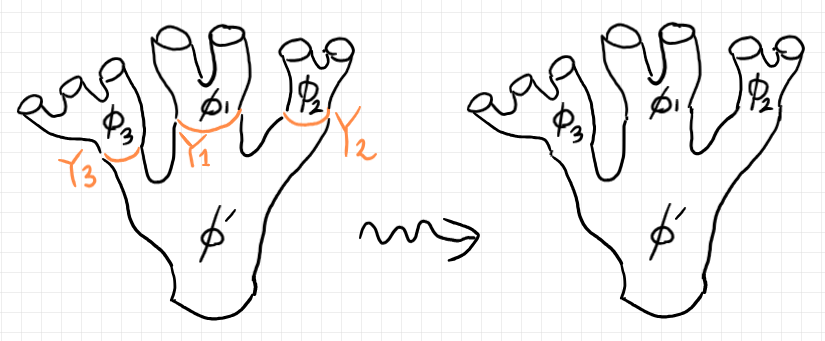
ちなみに、シームを消してしまうと、バエズ/ドーラン・ツリーは7本指の指出し手袋のような形に変形できて、それは (7 + 1) = 8 つ穴あき球面と同相です。
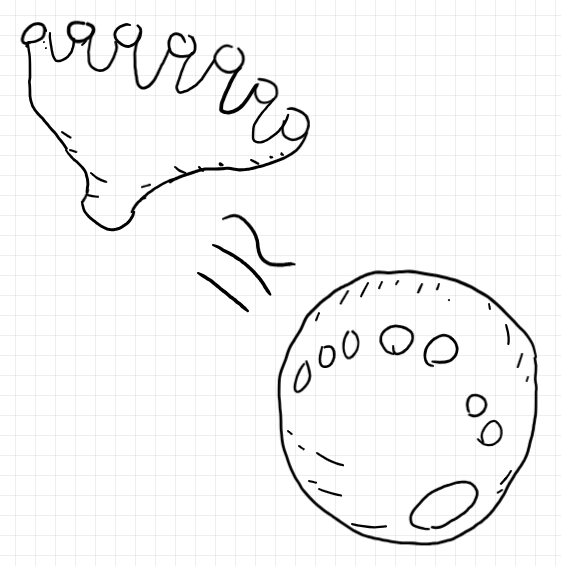
シームを消し去る操作を円板表示で表すなら次のようです。
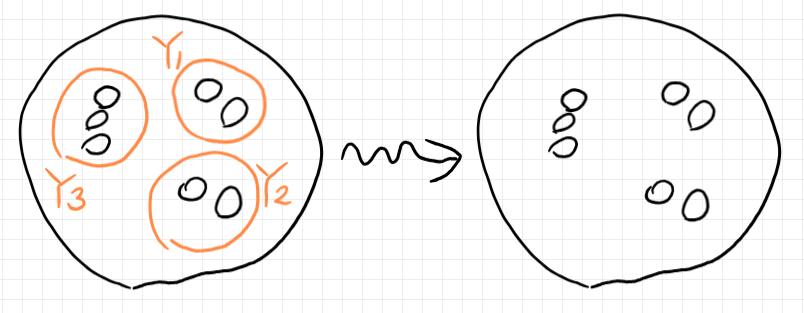
内側の小さいサークルのグルーピングに使っていた中間サークル〈middle circle〉を消していることになります。あるいは、入れ子を平坦化〈flatten〉しています*2。
スポットとボーダー
バエズ/ドーラン・ツリーを平面内に押し込めて表示するために円板表示を使ってますが、矩形〈方形〉表示でもかまいません。マルか四角かは本質的ではありません。「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」では四角い板をキャンバスに使っていました。例えば以下のように。
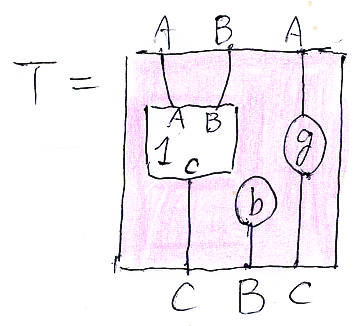
板の部分をピンクに塗って、穴は白抜きにしています。この絵のなかで $`g, b`$ などとラベルされているノードは穴ではなくて中身が詰まっています。穴ではないが、ワイヤリングで接続される対象物となるモノはスポット〈spot〉と呼びます。
先に出したバエズ/ドーラン・ツリー $`A`$ の穴のひとつを埋めてスポットにした $`A'`$ は次のように円板表示できます。$`G`$ とラベルされた緑に塗った部分がスポットです。
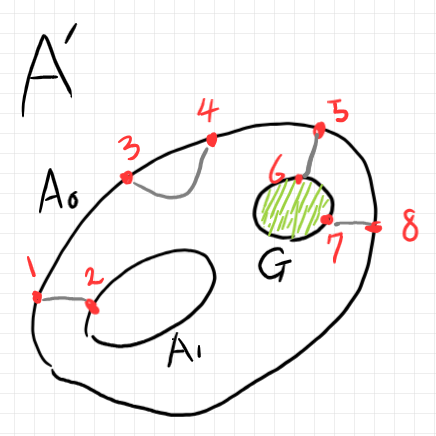
標準表示なら次のように描けます。
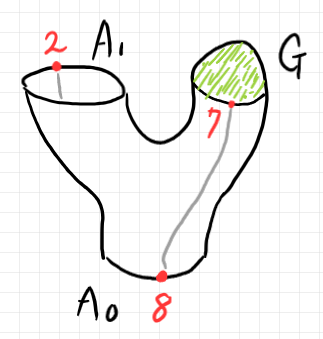
位相的な性質は変えない変形で次のような形にも描けます。円筒形ですね。スポットは円筒の側面の模様として描かれています。
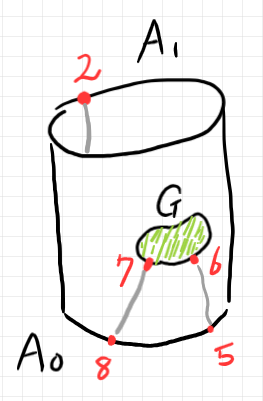
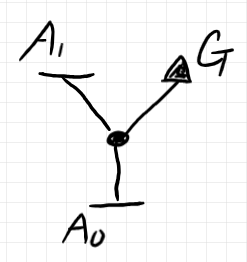
要約ツリーでは、スポットは黒三角で描くことにします。$`A'`$ の要約ツリーは次のようになります。
「入れ子の半グラフとバエズ/ドーラン・ツリー」では、ボーダーの定義を次のように書きました。
境界上のポート達とその修飾(型や極性)を含めた情報を(ボックスの)ボーダー〈border〉と呼ぶことにします。ボーダーは境界の幾何的形状ではなくて、組み合わせ的情報です。
図形としての円周よりはポートに注目して「ボーダー」と呼んだのですが、ポートを載せている図形とポート達を含めた概念としてボーダー〈border〉を使うことにします。その意味で、スポットを囲む円周とポート達もボーダーです。結局、ボーダーはニ種類あることになります。
- 境界円周とポート達
- スポットの縁とポート達
円板内部の穴が代入可能な変数に相当し、スポットは代入できない定数に相当します。どちらもボーダー情報としてのプロファイル〈インターフェイス | タイプ〉を持ちます。
バエズ/ドーラン・ツリーの高さ
バエズ/ドーラン・ツリーの高さ〈height〉は原則的に 1 です。高さだけを考えたいなら、要約ツリーを見たほうが(余計なモノがないので)分かりやすいでしょう。例えば、次の要約ツリー:
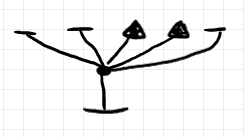
このツリーは、3つのリーフ円周、2つのスポットがワイヤリングされてルート円周に至ることを示しています。この形状のツリーを高さ 1 とします。
高さ 0 のツリーもあります。次は、リーフ円周が存在しないバエズ/ドーラン・ツリーの円板表示とその要約ツリーです。要約ツリーに、ワイヤリング(黒丸)とルート(横棒)しかないので高さは 0 です。
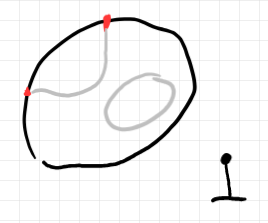
しかしときに、次のような要約ツリーを描くことがあります。これは高さ 3 です。
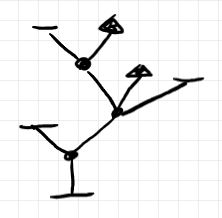
高さが 2 以上の要約ツリーを見たら、それはシームが省略されていると解釈します。シームをオレンジ色の棒として描き足すと次のようになります。
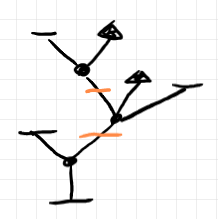
要約ではない標準表示だと、例えば以下のようです。
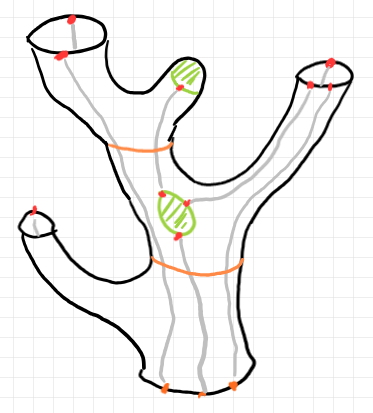
以前の例を再度出すと、以下のような高さ 2 の要約ツリーは、その下のシームツリーと同じことです。

注意点のまとめ
- バエズ/ドーラン・ツリーの標準表示の形状〈輪郭〉は、位相的には、(n + 1)個の穴あき球面と同型である。
- 穴の実体はないが、穴と境界円周は一対一対応するので、穴を境界円周と同一視してよい。
- 穴〈境界円周〉とスポットは別物である。スポットは穴ではなくて中身が詰まっている。
- スポットもポート(ワイヤーの接続点)を持つ。(必ず持つとは言ってない。)
- ポートが載っている1次元図形(とポートの情報)を総称的にボーダーと呼ぶので、穴〈境界円周〉もスポットもボーダーを持つ。
- 複数のバエズ/ドーラン・ツリーを、シーム〈縫い目〉により繋ぎ合わせることができる。
- シーム付きツリーとシームレスツリー〈seamless tree〉(通常の単一のツリー)は別物である。シーム付きツリーからシームレスツリーを得るには、シームを消し去る操作が必要。
- 通常のバエズ/ドーラン・ツリー、つまりシームレスツリーの高さは 1 か 0 である。高さ 2 以上のツリーはシーム付きツリーである。
- 要約ツリーでは、明示的にシームを描かないかも知れないが、高さ 2 以上ならシーム付きツリーと解釈する。
用語法
バエズ/ドーラン・ツリーを3次元のパイプ・ツリーで描くか、円板・円周で描くか、四角形・四辺形で描くかで、若干用語の違いがあります。
| ツリー | 円板 | 四角 |
|---|---|---|
| 境界円周 | 境界円周〈サークル〉 | ボックス |
| ルート境界円周 | 外部サークル | キャンバスボックス |
| リーフ境界円周 | 内部サークル | 内部ボックス |
| スポット | ソリッドディスク | (これもボックスか?) |
| ボーダー | ? | ? |
| シーム | 中間サークル | 中間ボックス |
| シーム付きツリー | 星座図 | 入れ子ワイヤリング図 |
我々は、「スポット」「ボーダー」を、円板や四角で描くときにも使います。
次の用語は描画法によらず共通です。
- ワイヤー
- ポート
- 穴
余談
ツリーや円板により何かを表すことは、十数年前からよく話題にしていたんですよね。2009年のセミナーのときのホワイトボードの写真が「モニャドセミナー2の資料やら補足やらナニヤラ」にあります。
豚さんやムンクの「叫び」をよく例題にしていました。
