2ヶ月半ほど前に「半グラフからシステムの記述へ」という記事を書きました。半グラフ(関連記事へのリンクは「スケマティック系のハブ記事 // 半グラフ」)は、ワイヤーに向きがないワイヤリング図/ストリング図だと思ってかまいません。無向ワイヤリング図/ストリング図はソフトウェアシステム(特にデータベースシステム)の記述に使えます。
昨日の記事「亜群をベースとする圏類似構造: コステロの事例」で、ケビン・コステロ〈Kevin Costello〉が定義した“グラフの圏”を紹介しました。コステロの“グラフ”とは半グラフのことです。“グラフの圏”は、半グラフが射になっている圏です。ほんとに圏になっているかは怪しいのですが、実用上そこを気にする必要はありません。
コステロの定義した“半グラフを射とする圏”は、システム記述にとても都合がよく使いやすそうです。システム記述の観点から、コステロの半グラフ圏を見てみます。$`\newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\In}{\text{ in } }`$
内容:
半グラフ
次は半グラフの例です。
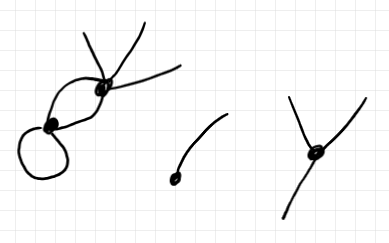
3つの半グラフではなくて、ひとつの半グラフです。3つの連結成分〈connected component〉を持ちます。辺〈無向辺〉は、外部辺〈external edge〉と内部辺〈internal edge〉に分けられます。内部辺は2本の半辺〈half-edge〉が一緒になったものだとみなします。それに対して、外部辺は1本の半辺だけでできています。
ここで扱う半グラフは、有限の頂点と辺(外部辺または内部辺)を持ち、多重辺(2つの頂点のあいだに複数の辺)も自己ループ辺も認めます。空な半グラフや単一の頂点だけの半グラフもあります。コステロの定義では、無頂点辺と無頂点ループは認めていません。半グラフは連結である必要はありません。どんな半グラフも、幾つかの連結成分に一意的に分解できます。
ひとつの半グラフや幾つかの半グラフについて語るとき、半グラフそのものと頂点・半辺・連結成分にラベルを付ける必要があります。上の半グラフにラベルを付けたものが以下です。
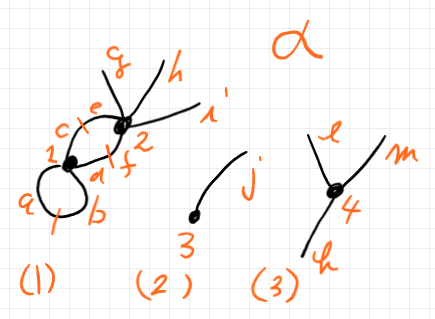
ここでのラベル付けのルールは:
- 半グラフはギリシャ文字小文字でラベルする。上の例では α 。
- 頂点は番号でラベルする。番号は単なる識別子で、頂点のあいだに順序はない。上の例では 1, 2, 3, 4 。
- 半辺はラテン文字小文字でラベルする。ひとつの内部辺は2つの半辺となる。上の例では a, b, ‥‥, m 。
- 連結成分は丸括弧で囲まれた番号でラベルする。上の例では (1), (2), (3) 。
ここで使ったラベルは、半グラフ・頂点・半辺・連結成分を識別する目的の名前で、型や色ではありません。今回扱う半グラフには、型・色などの修飾は一切ありません。単に形状を持つだけです。実際のシステム記述に使うときは、形状以外の情報が必要になりますが、それは別に考えます。
半グラフ圏
コステロは半グラフを単に「グラフ」と呼び、半グラフを射とする圏を $`{\bf Graphs}`$ としています。しかし、通常単に「グラフ」というと有向グラフのことで、$`{\bf Graph}`$ は有向グラフを対象とする圏です。紛らわしいので、コステロの半グラフ圏を $`{\bf CSemiGraph}`$ とします。
集合圏は集合を対象とする圏ですが、関係圏は関係を射とする圏です。なので、半グラフを射とする圏を半グラフ圏と呼ぶのはまーいいでしょう*1。しかし、半グラフを対象とする圏もあるし、半グラフの定義が色々あります(「半グラフの様々な定義」参照)。よって、先頭にコステロ〈Costello〉の"C"を付けておきます。
「亜群をベースとする圏類似構造: コステロの事例」で述べたように、素朴な定義だと、$`{\bf CSemiGraph}`$ は圏にはなりません。圏類似構造として定義するか、あるいは、半グラフの集合(大きい集合=類)に同値関係を入れて商集合を作って圏にする方法があります。今回は、そこは気にしないことにします。$`{\bf CSemiGraph}`$ は圏のように扱って問題ありません。
コステロのもとの定義では、射としての半グラフの域・余域($`{\bf CSemiGraph}`$ の対象)は有限バンドル(「亜群をベースとする圏類似構造: コステロの事例」参照)ですが、ここでは絵に描きやすいように、半グラフの域・余域もまた半グラフだとします。ただし、特別な形の半グラフです。
頂点がひとつだけで内部辺(自己ループ辺)を持たない半グラフをカローラ〈corolla〉と呼びます。連結成分がすべてカローラである(同じことだが、カローラを寄せ集めた)半グラフはカローラ林〈corolla forest〉です。単一のカローラも連結成分が1つのカローラ林とみなせます。
射としての半グラフの域・余域はカローラ林になります。つまり、圏 $`{\bf CSemiGraph}`$ の対象はカローラ林です。
- $`\mrm{Mor}({\bf CSemiGraph})`$ : すべての半グラフの集合(大きい集合)
- $`\mrm{Obj}({\bf CSemiGraph}) = |{\bf CSemiGraph}|`$ : すべてのカローラ林の集合(大きい集合)
圏の構造を与える、域・余域・結合・恒等に関しては、この後で、システム記述と関連させながら述べます。
システム設計図
半グラフを、システム記述の観点からシステム設計図〈system blueprint〉とも呼ぶことにします。実際、データベースの概念的仕様であるER図などは、半グラフの形状をしています(形状以外の情報を含みますが)。
半グラフの構成素は、システム記述における対応物を持ちます。
| 半グラフ | システムの設計図 |
| 頂点 | ソフトウェアコンポネント・ノード |
| 内部辺 | ソフトウェアコンポネント間の接続 |
| 外部辺 | システムの外部インターフェイス |
| 連結成分部分半グラフ | 独立サブシステムの設計図 |
| 連結成分 | ブラックボックス化した独立サブシステム・ノード |
半グラフの連結成分は、独立サブシステムとみなします。異なる独立サブシステムどうしは、切り離されているので互いに無関係です。連結成分は、部分半グラフ(サブシステム設計図)とみなすときと、中身が見えないノードとみなすときがあります。この2つの見方は、半グラフ〈システム設計図〉の結合のときに重要な役割を演じます。
「インターフェイス」、「仕様」、「指標〈シグネチャー〉」、「プロトタイプ」、「プロファイル」などの言葉はほぼ同じ意味です。完全な同義語として使う場合もあれば、微妙な差を付けることもあります。ここでは、インターフェイス、指標、プロファイルを次のように使います。
| 半グラフの外部辺の集合 | システムの外部インターフェイス |
| 連結成分部分半グラフの外部辺の集合 | 独立サブシステムのインターフェイス |
| 頂点の半辺の集合 | コンポネントのインターフェイス |
インターフェイスは半辺(外部辺も半辺とみなせる)の集まりを意味します。
| カローラ林 | 指標 |
| 連結成分達のカローラ林 | 外部指標 |
| 頂点達のカローラ林 | 内部指標 |
| 頂点のカローラ | コンポネントのプロファイル |
指標はカローラ林の意味です。カローラ林はカローラから構成されますが、ひとつのカローラは特にプロファイルと呼びます。カローラ林はカローラの集合なので、指標はプロファイルの集合です。一方で、単一のカローラもカローラ林なので、プロファイルも(シングルトンの)指標とみなせます。
半グラフ〈システム設計図〉の域・余域はどちらもカローラ林(圏 $`{\bf CSemiGraph}`$ の対象)ですが、域は内部指標、余域が外部指標となります。この事情を次節で詳しく見ましょう。
システム設計図の外部指標と内部指標
システム設計図〈半グラフ〉の外部指標〈余域〉とは、システム内の独立サブシステムの内部構造(それがあれば)をブラックボックス化〈blackboxing〉して隠蔽し、外部インターフェイスだけを提供した略式の設計図〈カローラ林〉です。先に出した半グラフ〈システム設計図〉α を再掲します。α の外部指標を考えましょう。

独立サブシステム〈連結成分部分半グラフ〉 (2), (3) は、単一のコンポネント〈頂点〉だけからなるので、隠蔽すべき内部構造はありません。独立サブシステム〈連結成分部分半グラフ〉 (1) は内部構造を持ちます。(1) 複数コンポネントを持ち、それらのあいだに接続関係があります。この内部構造を潰して単一のブラックボックス・ノード〈頂点〉にします。すると次のようになります。
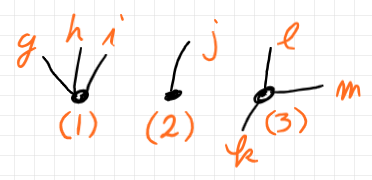
外部インターフェイス(外部辺の集合)はもとと変わりませんが、独立サブシステム (1) の構造は見えなくなっています。独立サブシステムが内部構造を持っていた((1) のように)か、単なるコンポネントだった((2), (3) のように)かはもう分かりません。
システム設計図〈半グラフ〉の内部指標〈域〉はというと、コンポネント〈頂点〉をすべて開示しますが、コンポネントの接続情報は捨ててしまった(漏らさない)略式の設計図〈カローラ林〉です。接続情報(内部辺の情報)が無いので、コンポネント〈頂点〉をパランパランに列挙しただけになります。次のように。
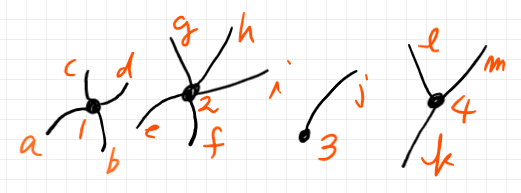
今説明したように、システム設計図〈半グラフ〉 α が当該の内部指標〈域のカローラ林〉と外部指標〈余域のカローラ林〉を持つことを、圏論の記法では次のように書きます。
$`\quad \alpha : \mrm{dom}(\alpha) \to \mrm{cod}(\alpha) \In {\bf CSemiGraph}`$
内部指標(素材)と外部指標(目的)が前もって与えられて、システム設計図〈半グラフ〉を構成することは、内部指標に列挙されているコンポネント達をうまく組み合わせて、外部指標に合致するように独立サブシステム(の設計図)達を作り上げる作業になります。
システム設計図の結合と恒等
前節で述べたことを一枚の絵にまとめると次のようになります。
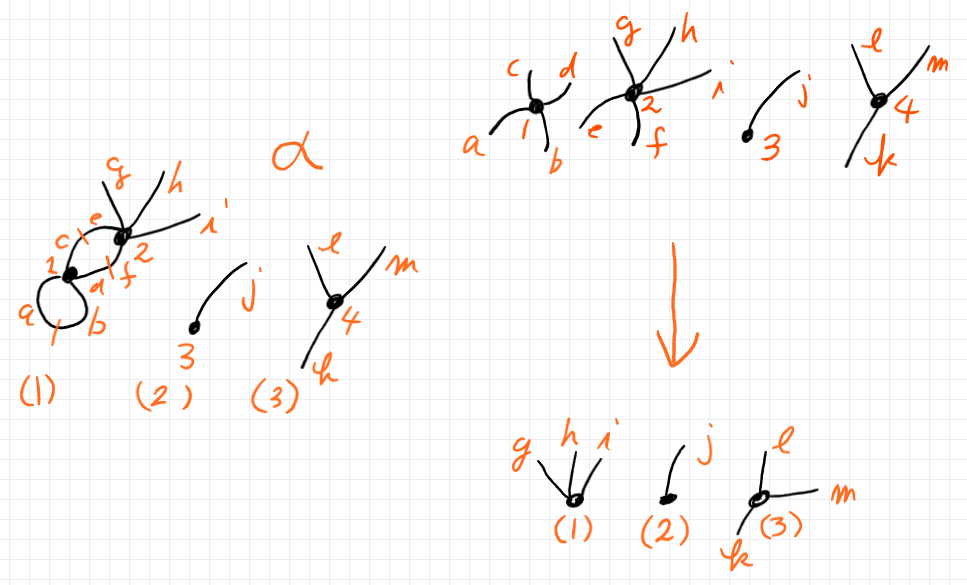
左側の半グラフ〈システム設計図〉 α は圏 $`{\bf CSemiGraph}`$ の射であり、上段のカローラ林〈内部指標〉が域で、下段のカローラ林〈外部指標〉が余域です。
ここで、もうひとつの半グラフ〈システム設計図〉 β を登場させます。
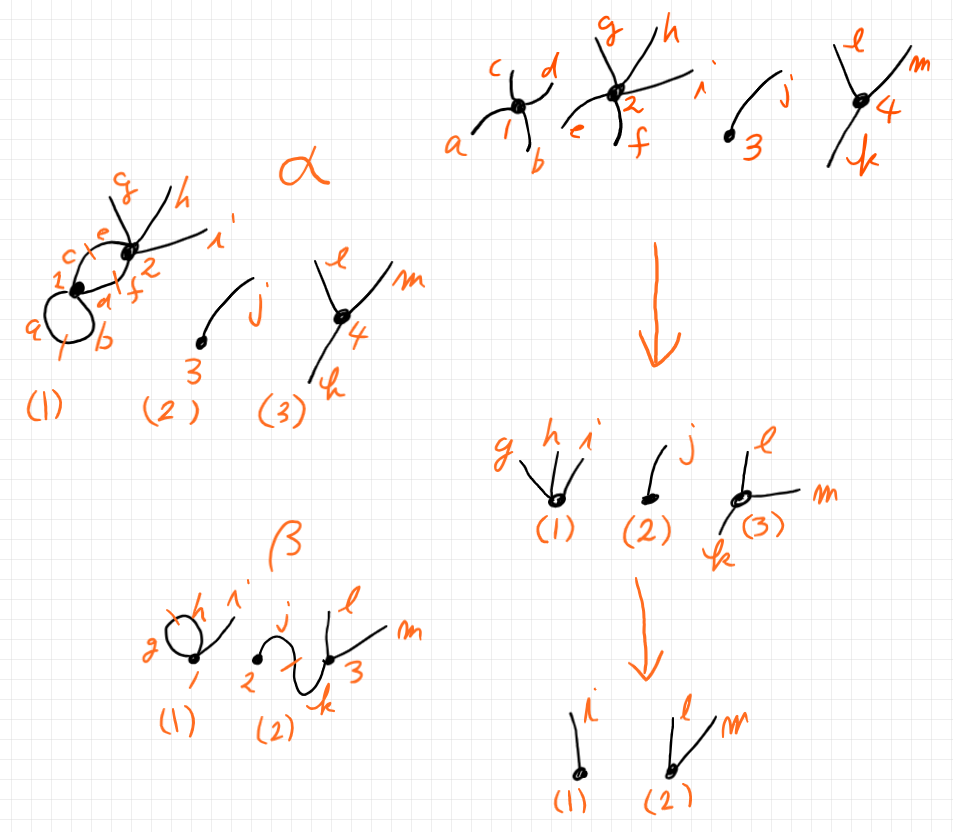
半グラフ β の域であるカローラ林は、半グラフ α の余域と“一致する”とします。ここで注意すべきは、α の連結成分を潰した頂点(ブラックボックス・ノード)と β の頂点を同一視することです。絵で言えば、β の頂点 1, 2, 3 と α の余域の頂点 (1), (2), (3) を同一視します。そうすると、圏における結合可能性〈composability〉の条件(下)を満たします。
$`\quad \mrm{cod}(\alpha) = \mrm{dom}(\beta)`$
α と β のこの順での結合の結果を γ と置きましょう。
$`\quad \gamma := \alpha \,; \beta \In {\bf CSemiGraph}`$
γ を作るには次の手順を実行します。
- β の頂点 1, 2, 3 を、α の連結成分部分半グラフ〈独立サブシステム設計図〉(1), (2), (3) で置き換える。
この操作はグラフ置換〈graph substitution〉とも呼ばれます。実際に頂点 1, 2, 3 を部分半グラフ (1), (2), (3) で置き換えると次のようになります。この例では、頂点 2, 3 の置き換えは何もしないのと一緒です。
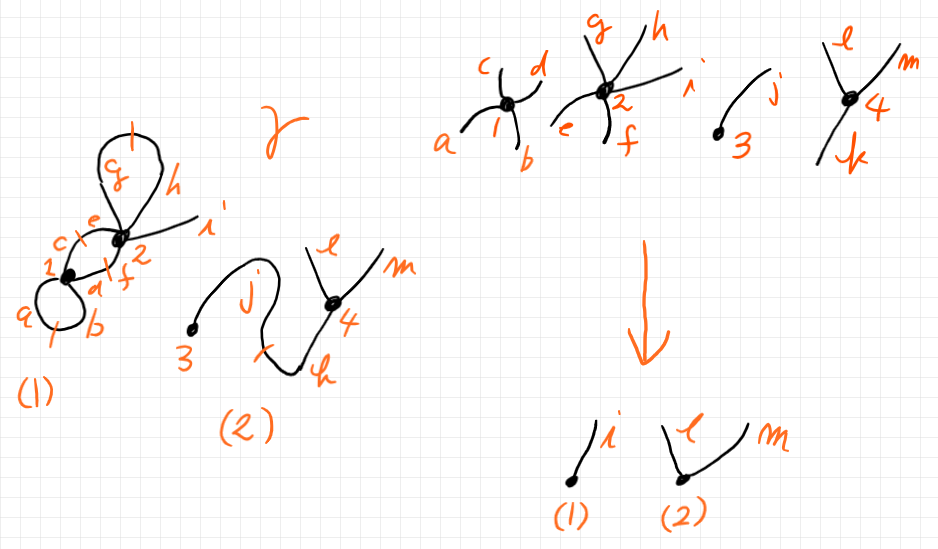
γ の域は α の域で、γ の余域は β の余域になっています。
$`\quad \gamma : \mrm{dom}(\alpha) \to \mrm{cod}(\beta) \In {\bf CSemiGraph}`$
圏 $`{\bf CSemiGraph}`$ の対象はカローラ林でした。カローラ林は半グラフでもあるので、そのまま 圏 $`{\bf CSemiGraph}`$ の射ともみなせます。対象であるカローラ林 $`\varphi`$ の恒等射は、射とみなした $`\varphi`$ です。次が成立します。
$`\quad \mrm{id}_\varphi = \varphi : \varphi \to \varphi \In {\bf CSemiGraph}`$
おわりに
ここで出した半グラフは、頂点と辺からなる形状だけで、修飾(付加的情報)はまったく持ってませんでした。実際のシステム記述ではもちろん、様々な修飾をほどこします。それにともない構造は複雑になります。その場合でも、複雑な構造を載せる下部構造・土台である形状の操作が $`{\bf CSemiGraph}`$ でキチンと定義されていれば安心感があります。
コステロが $`{\bf CSemiGraph}`$ (彼の記法では $`{\bf Graphs}`$)を定義したのは、オペラッド、巡回オペラッド、モジュラーオペラッドを統一的に扱う道具としてです。対称モノイド構造を与えた $`{\bf CSemiGraph}`$ から適当な対称モノイド圏への対称モノイド関手がモジュラーオペラッドになります。この発想は、ローヴェアの関手意味論であり、半グラフ圏 $`{\bf CSemiGraph}`$ がローヴェア・セオリーの役割を担っています(「ローヴェア・セオリーとその周辺」参照)。このことから、システム記述をローヴェア・セオリーのフレームワークに載せる道筋も見えてきます。
*1:「ナントカ圏」というネーミングに一貫性はありません。例えば、ハイパーグラフ圏(「ハイパーグラフ圏 一瞥」参照))は、ハイパーグラフを対象とする圏でもないし、ハイパーグラフを射とする圏でもありません。