念のため、「* -- toward 量子と古典の物理と幾何@名古屋」シリーズの目的を確認しておきます; これらの記事は事前の予備知識という意味はまったくありません。むしろ逆で、事後の参考情報として書いています。
限られた時間内のチュートリアルだと、最初から割愛せざるを得ない内容や、時間の都合(あるいは段取りの悪さ)からしゃべれない事項がたくさん出てきます。そういった背景や周辺に関する情報が後々参照できればいいと思います。しかし、実際に事後になってそういうことを書くのはモチベーション的に困難です。そこで、事前に事後情報を書き溜めておこう、ということです。
今回は、ストリング図の描画法をある程度標準化しようという話です。平面内にストリング図を描くとき、ノードの位置(x座標, y座標)を決める基準を定めます。またこれは、ストリング図のテキスト・エンコーディングの標準化手法にもなります。
図を入れてないので、後で図を入れるかも知れません。[追記]図を入れました。[/追記]ちなみに、ストーリーを組み立てるためのピースはあと2つ; とある代数系の話と高次関手の構成法です。
内容:
ストリング図と簡易ストリンググラフ
圏論的な絵算(categorical pictorial/graphical/diagrammatic calculation)ではストリング図(string diagram)と呼ばれる図を使います。ストリング図はほぼ有向グラフですが、グラフ理論におけるグラフとは微妙に異なります。ストリング図をグラフ理論の言葉で定式化した概念として、ディクソン/ダンカン/キッシンジャー(Lucas Dixon, Ross Duncan, Aleks Kissinger)のストリンググラフ(string graph)があります。
ここでは、ストリンググラフの定義を簡易化した簡易ストリンググラフを使います。オリジナルのストリンググラフについて知っている必要はありませんが、興味があれば次の記事をどうぞ。
簡易ストリンググラフはグラフ理論的(あるいは組み合わせ的)な概念です。圏論的なストリング図は、簡易ストリンググラフに、描画(rendering)とラベリング(labeling)を付加した概念です。
単なる有向グラフ(箙〈えびら〉)は、2つの集合V, Eと2つの写像 src:E→V, trg:E→V で決まる組(V, E, src, trg)です。Vは頂点(vertex)の集合、Eは辺(edge)の集合で、srcとtrgは辺にそれぞれ始点(source vertex, 始頂点)と終点(target vertex, 終頂点)を対応させる写像です。これから考える(有向)グラフは、VもEも有限集合と仮定します。
G = (V, E, src, trg) をグラフ(箙)として、v∈V に対して、OutG(v), InG(v) を次のように定義します。
- OutG(v) := {e∈E | src(e) = v}
- InG(v) := {e∈E | trg(e) = v}
Out/Inどちらも辺の集合です。Out/Inを使って、出次数(out-degree)と入次数(out-degree)を定義します。
- out-degG(v) := card(OutG(v))
- in-degG(v) := card(InG(v))
card(-)は、集合の基数(cardinality、濃度)を取る写像とします。グラフが有限なので、出次数/入次数ともに有限(自然数)です。下付きのGは、それが明らかなら省略します。
簡易ストリンググラフ(reduced string graph)とは、頂点の集合Vを2種類に分けたグラフです。V = NodeV + WireV ('+'は集合の直和)。NodeVに所属する頂点をノード頂点(node vertex)、WireVに属する頂点をワイヤー頂点(wire vertex)といいます。簡易ストリンググラフが満たすべき条件は次です。
- ワイヤー頂点の(in-deg, out-deg)の組み合わせは、(0, 1), (1, 1), (1, 0)のいずれかに限る。
- ノード頂点vのIn(v), Out(v)に、全順序(線形順序)構造が入っている。
以上の簡易ストリンググラフの定義は、オリジナルのストリンググラフの定義とは異なります。非対称モノイド圏(対称性を仮定しないモノイド圏)で使うストリング図だけに用途を限定して、オリジナルの定義を簡略化したものです。この定義では、多重辺、自己ループ辺などを許してます(オリジナルの定義では多重辺/自己ループ辺を許しません)。
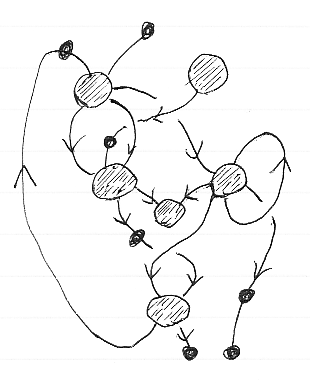
図の説明
オダンゴがノード頂点、小さな黒丸がワイヤー頂点です。多重辺、自己ループ辺、サイクルを許します。ワイヤー頂点を持たない辺(両端がノード頂点)も許します。この例で辺が交差しているのは、グラフが平面に埋め込めないことがある事を示唆します。平面に埋め込むには交差をノードに変えます。交差を表すノードはブレイド(braiding)や対称(symmetry)に対応するので、ブレイド付きモノイド圏、対称モノイド圏のストリング図が得られます。サイクル(自己ループ辺はサイクルの一種)は、圏のトレースに対応します。
ここから先では、簡易ストリンググラフを単にストリンググラフと呼びます。オリジナルの(ディクソン/ダンカン/キッシンジャーの)ストリンググラフとは定義が少し違うので注意してください。
ストリンググラフに関する基本事項
G = (NodeV, WireV, E, src, trg) をストリンググラフとします。ワイヤー頂点(WireVの要素)は、3種類に分類できますが、それらを次のように呼びます。
- (in-deg, out-deg) = (0, 1) であるワイヤー頂点を、進入境界頂点(incoming boundary vertex)、または入口頂点(entrance vertex)、または入力頂点(input vertex)と呼ぶ。
- (in-deg, out-deg) = (1, 1) であるワイヤー頂点を、内部ワイヤー頂点(interior wire vertex)と呼ぶ。
- (in-deg, out-deg) = (1, 0) であるワイヤー頂点を、退出境界頂点(outgoing boundary vertex)、または出口頂点(exit vertex)、または出力頂点(output vertex)と呼ぶ。
この記事では、「入口頂点、出口頂点」を使います。また、ストリンググラフのノード頂点は単にノードとも呼びます。ノードではない頂点(=ワイヤー頂点)もあることに注意!
Gの頂点(ワイヤー頂点またはノード頂点)と辺を互い違いに並べたシーケンス [v0, e1, v1, ..., en, vn] で、src(ei) = vi-1, trg(ei) = vi となっているものをGのパス(経路、道)といいます。v0をパスの始点、vnを終点、nをパスの長さとよびます。
パス [v0, e1, v1, ..., en, vn] であって、v0がノードか入口頂点、vnがノードか出口頂点、v1, ..., vn-1の全てがワイヤー頂点であるものをワイヤーと呼びます。どのワイヤー頂点も、唯一のワイヤーに所属します*1。
ある頂点から出て同じ頂点に戻るパスが存在しないとき、Gは非循環的(acyclic)といいます。この記事で扱うグラフは非循環的です。
有向グラフにおける最短距離と最長距離
この節の議論は、ストリンググラフでなくて単なる有向グラフでも通用します。G = (V, E, src, trg) は有向グラフとします。
v, w∈V として、vからwに至るパスの全体をPathG(v, w)と書きます。下付きのGは、それが明らかなら省略します。Gが有限でも循環的なら、Path(v, w)は無限集合になり得ます。Path(v, w)が空集合のときもあります。Path(v, v)は、vからvに戻るパスの集合です。Path(v, v)に属するパスをサイクルと呼びます。Gが非循環的なら、任意のvに対してPath(v, v)は空集合です。
グラフ内の2頂点v, wに対して、最短距離と最長距離を定義します。まず、最短距離min-dist(v, w)を定義します。
- min-dist:V×V→N∪{+∞}
- min-dist(v, v) = 0
- v ≠ w のとき、Path(v, w)が空集合なら+∞、そうでないなら min-dist(v, w) = (vからwへ至るパスの長さの最小値)
min-distは距離の公理の対称性を満足しませんが、非対称な距離にはなっています(「移動のコストとしての距離」参照)。
- min-dist(v, w) = 0 ⇔ v = w
- min-dist(u, w) ≦ min-dist(u, v) + min-dist(v, w)
最長距離max-dist(v, w)の定義は次のとおりです。
- max-dist:V×V→N∪{+∞}∪{-∞}
- Path(v, w)が空集合で v = w なら、max-dist(v, w) = 0
- Path(v, w)が空集合で v ≠ w なら、max-dist(v, w) = -∞
- Path(v, w)が空でない有限集合なら、max-dist(v, w) = (vからwへ至るパスの長さの最大値)
- Path(v, w)が空でない無限集合なら、max-dist(v, w) = +∞
最長距離は、逆三角不等式を満たします。
- max-dist(u, w) ≧ max-dist(u, v) + max-dist(v, w)
Gが単なる有向グラフではなくてストリンググラフのとき、min-dist, max-distを少し修正したnode-min-distとnode-max-distを定義します。
- node-min-dist:NodeV×NodeV→N∪{+∞}
- node-max-dist:NodeV×NodeV→N∪{+∞}∪{-∞}
であり、node-* ともとの定義との違いは、パスの長さの測り方だけです。node-* では、パス上に存在するワイヤー頂点は無視して長さを測ります。[v, e, w f, x] がパスで、wだけがワイヤー頂点なら、このパスの長さは2ではなく1とします。
非循環的ストリンググラフにおけるレベル関数
G = (NodeV, WireV, E, src, trg) をストリンググラフで非循環的だと仮定します。V = NodeV + WireV とします。Vはすべての頂点の集合です。この節では、ノード頂点の集合NodeVで定義された関数 level:NodeV→N を定義します。節の最後に図があるので、それを参照しながら読むとよいでしょう。
Top(G) := {v∈(NodeV + WireV) | in-deg(v) = 0} とします。Top(G)は入次数が0の頂点の集合です。Top(G)に入る頂点は、入口頂点(進入境界頂点)か入る辺を持たないノードです。Gが空でない非循環的有向グラフの場合、Top(G)は空ではありません(練習問題)。また、次の性質もあります(これも練習問題)。
- Top(G)に属さないGの任意の頂点vに対して、Top(G)のどれかの頂点からvに至るパスが存在する。
有向グラフ(としての)Gの頂点rがルート頂点(root vertex)であるとは次のことです。
- r以外のGの任意の頂点vに対して、rからvに至るパスが存在する。
一般に、Gにルート頂点があることは保証されません。レベル関数(関数level)の定義にはルート頂点があったほうが便利なので、Gに人為的にルート頂点を付け加えます。付け加える頂点はノード頂点として、仮想ルートノード(virtual root node)と呼ぶことにします。
与えられた非循環的ストリンググラフGに対して、仮想ルートノードを追加した新しいグラフG'を次のように定義します。
- G' = (NodeV', WireV', E', src', trg')
- NodeV' := NodeV + {r} (rはNodeVに含まれない要素)
- WireV' := WireV
- E' := E + {ew | w∈Top(G)} (詳細はすぐ後で)
- e∈E ならば src'(e) = src(e)、src(ew) = r
- e∈E ならば trg'(e) = trg(e)、trg(ew) = w
rが追加した仮想ルートノードです。Gの入次数が0である頂点wごとに、新しい辺ewを追加します。辺ewは、仮想ルートノードrから頂点wに至る辺です。
仮想ルートノードrから出る辺の集合Out(r)には適当な全順序を入れておきます。ストリンググラフの条件として次があったからです。
- ノード頂点vのIn(v), Out(v)に、全順序(線形順序)構造が入っている。
このようにして作ったG'(Out(v)の全順序も含めて)は、非循環的ストリンググラフになります。Out(v)の全順序の入れ方に任意性があるので、GからG'を一意的に作れるわけではありません。なお、Out(v)の全順序は後で使います。
Gから作った仮想ルートノードを持つ非循環的ストリンググラフG'を使って、関数 level:NodeV'→N を次のように定義します*2。
- level(v) := node-max-dist(r, v)
node-max-distは任意のグラフに対して定義可能ですが、+∞, -∞を許しています。しかし、levelには次の性質があります。
- 0≦ level(v) <+∞ (level(v)∈N)
まず、仮想ルートノードrから他の任意のノードvに至るパスが存在するので、node-max-dist(r, v) = -∞ は起こりません。また、任意のr, vに対してPath(r, v)は有限集合なので、node-max-dist(r, v) = +∞ も起こりません。よって、0≦ level(v) <+∞ です。
Path(r, v)が有限集合なのは、次の事実によります。
- Gが非循環的 ⇔ 任意の v, w∈V に対して、Path(v, w)は有限集合(空集合も含む)。
レベル関数の例を以下に示します。
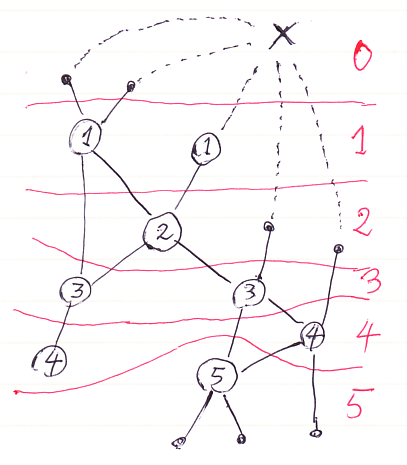
図の説明
バッテンは仮想ルートノードです。ノード内にレベルの値が書き込んであります。同じレベルのノードを1つの“層”として、赤線で層分けしています。レベル0の層は仮想ルートノードだけです。
ノード頂点の全順序
Gが非循環的ストリンググラフのとき、Gに含まれるノードを列挙したいことがあります。列挙には、集合NodeV上の全順序を必要とします。この節では、NodeV上の全順序を構成します。節の最後に図があるので、それを参照しながら読むとよいでしょう。
前節と同様に、仮想ルートノードrを追加した非循環的ストリンググラフG'で考えます。関数 genel:NodeV'→N を次のように定義します。
- genel(v) := node-min-dist(r, v)
仮想ルートノードrからvへのパスは存在するので、0≦ genel(v) <+∞ であり、genel:NodeV'→N はwell-definedです。genel(v)をノードvの世代番号と呼びます。仮想ルートノードから何代目の子孫かを表す非負整数です。関数genelの逆像を世代集合と呼びましょう。第k世代の世代集合GenelG'(k) は:
- GenelG'(k) := genel-1(k)
世代集合に関して次が成立します。
- GenelG'(0) = {r}
- GenelG'(1) = Top(G)
これから、GenelG'(0), GenelG'(1), GenelG'(2), ... のそれぞれに全順序を入れます。全順序の構成は数学的帰納法によります。以下に述べる構成で、G'お内部ワイヤー頂点は邪魔なので、(ストリング図のトポロジーを変えないように)内部ワイヤー頂点を取り除いておきます。内部ワイヤー頂点は、議論の本質に影響しません。
GenelG'(0)は単元集合なので、全順序は自明です。GenelG'(1)はTop(G)です。G'の作り方から、Top(G)とOut(r)は1:1対応します。Out(r)には全順序が入っているので、その順序をTop(G)に写してGenelG'(1)の全順序を定義します。
GenelG'(k)(k≧1)まで全順序が入ったと仮定します。GenelG'(k+1)が空集合ならやるべきことはありません。v, w∈GenelG'(k+1) とします。
- Parents(v) := {w∈NodeV' | src(e) = w, trg(e) = v となる辺eが存在する}
と定義すると、Parents(v)は空ではなく Parents(v)⊆GenelG'(k) となります。GenelG'(k)は帰納法の仮定より有限全順序集合なので、Parents(v)から最初の要素を取り出せます。その最初の要素を firstParent(v) とします。
- firstParent(v) < firstParent(w) なら、v < w と定義する。
- firstParent(w) < firstParent(v) なら、w < w と定義する。
firstParent(v) = firstParent(w) = u なら、さらに比較を続けます。uはv, wの共通の親ですから、PathG'(u, v), PathG'(u, w) は共に空ではありません。また、PathG'(u, v)⊆Out(u), PathG'(u, w)⊆Out(u) とみなせるので、Out(u)の全順序からPathG'(u, v), PathG'(u, w) も有限全順序集合となります。
PathG'(u, v), PathG'(u, w) の最初の要素をそれぞれ firstEdge(u, v), firstEdge(u, w) とします。
- firstEdge(u, v) < firstEdge(u, w) なら、v < w と定義する。
- firstEdge(u, w) < firstEdge(u, v) なら、w < v と定義する。
最後に、firstEdge(u, v) = firstEdge(u, w) のケースがありますが、このときは v = w です。
以上により、GenelG'(k+1)に全順序が入りました。結果としてに、任意の世代集合に全順序が入ることが分かりました。
世代番号の通常の順序と、各世代集合内の全順序を組み合わせると、ノード集合NodeV'に全順序が入ります。当然に、NodeV'の部分集合NodeV(Gのノード集合)にも全順序が誘導されます。
今までの構成法から次が言えます。
- 非循環的ストリンググラフGのTop(G)に全順序を入れれば、NodeVに全順序を入れることができる。
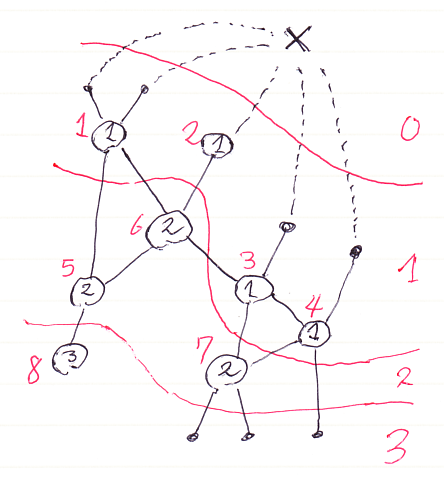
図の説明
バッテンは仮想ルートノードです。ノード内に世代番号の値が書き込んであります。同じ世代番号のノードを1つの“層”(世代集合)として、赤線で層分けしています。世代0の層は仮想ルートノードだけです。ノードの横に赤で書き込んである番号は全順序による通し番号です。世代番号が小さいノードが先に現れます。
レベル関数と全順序の利用
ストリンググラフはストリング図のグラフ理論的な表現です。ストリング図が与えられたとき、対応するストリンググラフを作り、それが非循環的なら上記の方法でレベル関数と全順序を構成できます。
平面上でのストリング図のレイアウトを標準化する際に、ノードのy座標をレベル関数の値にして、同じy座標のノード達のx座標をノード間全順序に従って設定することができます。
このように調整した平面ストリング図は、目視が楽なだけでなくて、モノイド圏の式としてのテキスト・エンコーディングも決まった手順でできます。
- レベルごとに、左から右の順で、ノード(射)またはワイヤー(恒等)のモノイド積を作る。
- すべてのレベルの項をレベルの大小の順序で結合する。