このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

述語論理： 様々な多圏達の分類整理

雑記／備忘

「自然演繹の再構築への道」という記事を書いたのは6年前です。それから折に触れて“自然演繹の再構築”について考えてはいますが、細部まで詰めているわけじゃないです。んで、また最近ちょっと考えている次第。

上記過去記事では、「モノイド圏から多圏を作って、その多圏をベースに形式的体系〈formal system〉を作るんだ」と言っています。この方針は今でも変わっていません。ここで問題は、多圏があまりポピュラーな概念ではなくて、テキスト〈教科書／参考文献〉も少ないことです。そもそも、「多圏」という言葉の定義が人により違い、コミュニケーションも困難です。

この記事では、様々な多圏を分類整理します。$`\newcommand{\cat}[1]{\mathcal{#1} }
\newcommand{\In}{\text{ in } }
\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\id}{\mathrm{id} }
%`$

内容：

ハブ記事：

複圏、余複圏、多圏

まず、複圏〈multicategory〉、余複圏〈comaulticategory〉、多圏〈polycategory〉についてすごく大雑把に説明します。n, m は任意の自然数（0 も許す）とします。

  • 圏 ： 圏の射は単一の入力（域の対象）と単一の出力（余域の対象）を持つ。
  • 複圏 ： 複圏の射はn個の入力と単一の出力を持つ。
  • 余複圏 ： 余複圏の射は単一の入力とn個の出力を持つ。
  • 多圏 ： 多圏の射はn個の入力とm個の出力を持つ。

射をストリング図で表すとき、入力は上側のワイヤー、出力を下側のワイヤーとして描くことにします。n入力-m出力の多圏の射は次のように描きます。

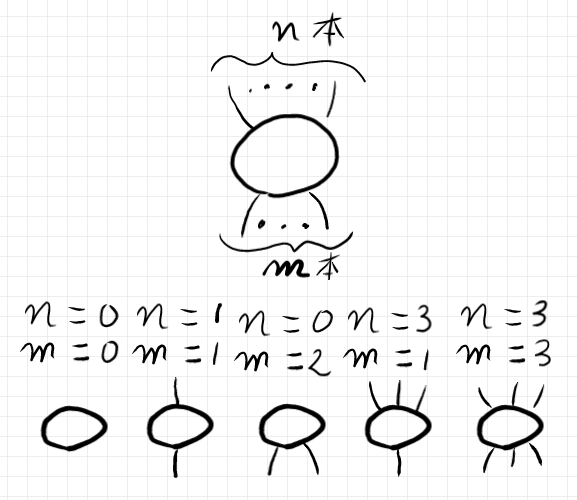
多圏の射は多射〈polymorphism | polyarrow〉と呼びます。（絵で描くと）入力のワイヤーがn本、出力のワイヤーがm本である多射を (n→m)-多射〈(n→m)-{polymorphism | polyarrow〉と呼ぶことにします。

かつて僕は、(n→m)-多射を描いた図をスパイダーと呼んでいました。が、用語「スパイダー」は特別な意味を持つ脚付きノードの意味で用いられるので、一般的な(n→m)-多射の図をスパイダーと呼ぶのはやめました -- ノードまたはボックスと呼んでます。

[補足]

The ZX-calculus では、ストリング図のZノード〈緑ノード〉とXノード〈赤ノード〉をスパイダーと呼んでいます。例えば次の論文参照。

  • Title : Interacting Quantum Observables: Categorical Algebra and Diagrammatics
  • Authors: Bob Coecke, Ross Duncan
  • Submitted: 25 Jun 2009 (v1), 21 Apr 2011 (v3)
  • Pages: 81p
  • URL: https://arxiv.org/abs/0906.4725

次に、「スパイダー付き圏」で紹介したモートンの論文を見てみましょう。

  • Title: Belief propagation in monoidal categories
  • Author: Jason Morton
  • Submitted: 12 May 2014 (v1), 30 Dec 2014 (v2)
  • Pages: 8p
  • URL: https://arxiv.org/abs/1405.2618

モートンのスパイダー圏〈spidered category〉の定義は、厳密対称モノイド圏であって、各対象 $`A`$ ごとに特殊可換フロベニウス構造 $`(A, m, u, \delta, \varepsilon, \sigma^F)`$ を備えたものです。ここで：

  • $`m`$ は可換乗法
  • $`u`$ は単位
  • $`\delta`$ は余可換余乗法
  • $`\varepsilon`$ は余単位
  • $`\sigma^F`$ は可換性の定義に使う対称射 $`A\otimes A \to A\otimes A`$

$`\sigma^F`$ が、圏がもともと持っている対称射と違ってもいいという定義です。しかし、すぐに $`\sigma^F = \sigma`$ の条件を付け加えて、さらにコンパクト閉構造も入れたダンジョン圏を定義しています。

ダンジョン圏におけるスパイダーとは、次の射達の（結合とモノイド積による）組み合わせである射です。

  1. 恒等射
  2. 対称射
  3. フロベニウス射（特殊可換フロベニウス構造を構成する射）
  4. コンパクト閉圏の双対構造を与えるカップ射とキャップ射

もうひとつ、パヴロヴィックの論文。

  • Title: Lambek pregroups are Frobenius spiders in preorders
  • Author: Dusko Pavlovic
  • Submitted: 7 May 2021 (v1), 6 Apr 2022 (v4)
  • Pages: 21p
  • URL: https://arxiv.org/abs/2105.03038

ここでもやはり、各対象ごとに特殊フロベニウス構造が載ったモノイド圏を考えます。スパイダーはフロベニウス射（特殊フロベニウス構造を構成する射）か、それらの組み合わせのことです。特に典型的な〈狭義の〉スパイダーは、フロベニウス構造の乗法から作られるn本のワイヤーの合流の後に、フロベニウス構造の余乗法から作られるm本のワイヤーへの分岐を繋いだ形のものです。

何をスパイダーと呼ぶかはケースバイケースですが、生成射〈generating morphisms〉の集合と組み合わせ方を決めて、生成射の組み合わせをスパイダーと呼ぶことになります。

[/補足]

用語に関する注意

圏に関して、射、域、余域、結合〈合成〉などの用語の意味はハッキリしています。通常の圏を単純圏〈simple category〉とも呼び、単純圏の対象を単純対象〈simple object〉と呼ぶことにします*1。次のような用語法なら整合的で覚えやすいですよね。現実は違うんですが。

射 域 余域 結合
単純圏 単純射 単一単純対象 単一単純対象 単純結合
複圏 複射 単純対象のリスト 単一単純対象 複結合
余複圏 余複射 単一単純対象 単純対象のリスト 余複結合
多圏 多射 単純対象のリスト 単純対象のリスト 多結合

現実的事情とここでの方針は：

  1. 単純圏という言葉は実際には使われていない。ここで概念の整理のために出しただけで、それほど使う機会はない。圏＝単純圏。
  2. 単純対象を色〈color〉と呼ぶことが多い。ここでも色は使う。
  3. 複圏はオペラッド〈operad〉と呼ぶことが多い。が、ここでは複圏と呼ぶ。
  4. 複射はオペレーター〈operator〉と呼ぶことが多い。が、オペレーターは別な意味や一般的な語として使われることがあるので、ここでは複射〈multimorphism | multiarrow〉と呼ぶ。
  5. 複結合はオペラッド結合〈{operadic | operad} composition〉と呼ぶことが多い。がここでは複結合〈multicomposition〉と呼ぶ。
  6. 余複圏は話題になることが少ない。
  7. 多圏には幾つかの変種〈バリアント〉があり、プロペラッド〈properad〉、プロップ〈PROP〉、両オペラッド〈dioperad〉などの呼び名がある。これについては後で分類する。総称としては多圏を使う。
  8. 多射を意味する "polymorphism" が「多相」とかぶるので、"polyarrow", "polymap" などが使われる。が、日本語で「多射」と「多相」はかぶらないので、ここでは多射を使う。
  9. 多結合は後でナロー多結合とワイド多結合に分ける。総称は多結合〈polycomposition〉を使う。

ワイヤリング規律による分類

ガーナー／フーショウィッツの次の論文で、多圏と関連する構造が扱われています。

  • Title: Shapely monads and analytic functors
  • Authors: Richard Garner, Tom Hirschowitz
  • Submitted: 18 Dec 2015 (v1), 10 Oct 2017 (v3)
  • Pages: 52p
  • URL: https://arxiv.org/abs/1512.05980

多圏の多射をストリング図で表すとして、ワイヤーに対する操作を基準に多圏を分類しています。視覚的・図形的直感に訴えるので、分かりやすい分類基準になります。分類基準は次の3つです。

  1. 対称 vs. 非対称 ： ワイヤーの入れ替え（置換群による作用）を許すか？ 許すなら対称〈symmetric〉、許さないなら非対称〈non-symmetric〉。
  2. モノイド vs. 非モノイド ： 2つのノードを横に並べる配置〈juxtaposition〉を許すか？ 許すならモノイド〈monoidal〉、許さないなら非モノイド〈non-monoidal〉。
  3. ワイド vs. ナロー ： 2つのノードのワイヤーを繋ぐ（多結合する）とき、任意の本数のワイヤーの接続を許すか？（それとも1本だけに限定するか？） 許すならワイド〈wide〉、許さないならナロー〈narrow〉。

以上のような、ワイヤリングと配置に関する「許す／許さない」の規則・基準をワイヤリング規律〈wiring discipline〉といいます。絵で簡単に説明すると：

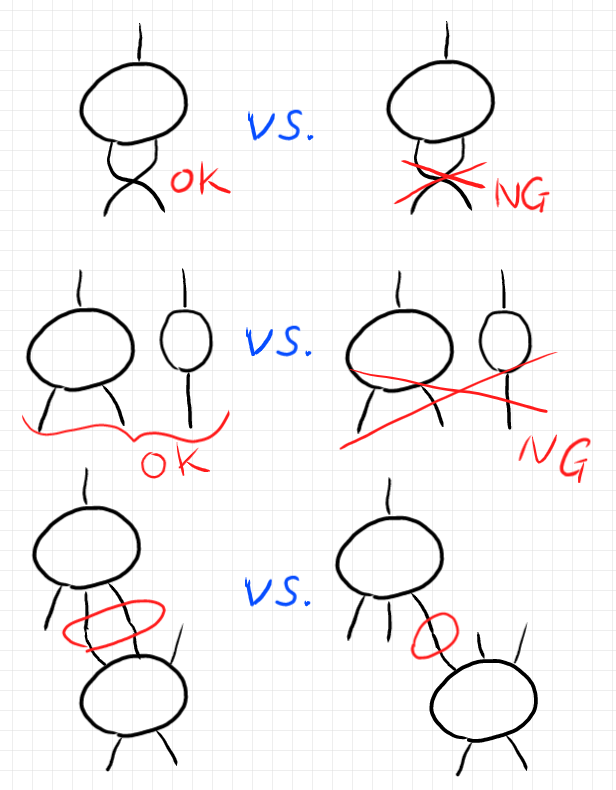
多圏が対称なら、n本のワイヤーの並びに、n次対称群〈置換群〉の要素を作用させてよいので、任意の並べ替えができます。非対称ではそれが許されません。

多圏がモノイド〈monoidal〉なら、2つのノードを横に並べたものをひとつのノードとして扱えます。このときワイヤーのリストは連接されます。非モノイド〈non-monoidal〉多圏ではノードを横に並べる操作はできません。別な言い方をすると、非モノイド多圏の多射をあらわすストリング図は、図形として連結でなくてはなりません。

同じ色のワイヤーを繋ぐことが多結合ですが、多圏がワイド（ワイド多結合を許す）なら、任意本数のワイヤーの束をまとめて繋ぐことができます。ナローな多圏では1本のワイヤーしか繋ぐことができません。

多圏の基本概念

多圏の記述に際して、通常の圏〈単純圏〉となるべく同じく記法を使います。$`\cat{P}`$ を多圏としたとき、色〈単純対象〉の集合を $`|\cat{P}|`$ とします。色のリストの集合を $`|\cat{P}|^*`$ とします。右肩の星はクリーネスターです。

$`A, B\in |\cat{P}|^*`$ に対して、ホムセットは $`\cat{P}(A, B)`$ と書きます。多圏のホムセットであることを強調したいときは多ホムセット〈polyhomset〉といいます。もちろん、多ホムセットは多射の集まりです。$`f\in \cat{P}(A, B)`$ であることを、圏の場合と同じく次のように書きます。

$`\quad f:A \to B \In \cat{P}\\
\quad \mrm{dom}(f) = A, \; \mrm{cod}(f) = B
%`$

リストを成分で書くなら：

$`\quad f\in \cat{P}( (A_1, \cdots, A_n), (B_1, \cdots, B_m) )\\
\quad f:(A_1, \cdots, A_n) \to (B_1, \cdots, B_m) \In \cat{P}\\
\quad \mrm{dom}(f) = (A_1, \cdots, A_n), \; \mrm{cod}(f) = (B_1, \cdots, B_m)
%`$

$`X\in |\cat{C}|`$ に対して、恒等射 $`\id_X \in \cat{P}( (X), (X) )`$ が定義されます。ここで注意すべきは、$`A\in |\cat{C}|^*`$ に対して $`\id_A`$ が定義できるとは限らないことです。多圏 $`\cat{P}`$ が非モノイド〈non-monoidal〉なら、図形として連結でない多射は禁止されるので、複数のワイヤーを離して並べた形状の $`\id_A`$ は作れません。

次のような多射があるとします。

$`\quad f:(A_1, \cdots, A_n) \to (B_1, \cdots, B_m) \In \cat{P}\\
\quad g:(C_1, \cdots, C_p) \to (D_1, \cdots, D_q) \In \cat{P}
%`$

多結合がナロー多結合〈narrow polycomposition〉、つまり1本のワイヤーしか繋げないとして、$`f, g`$ の順で多結合可能なケースが2つあります。

  1. $`B_1 = C_p`$ ： $`f`$ の最初の出力ワイヤーと、$`g`$ の最後の入力ワイヤーの色が一致
  2. $`B_m = C_1`$ ： $`f`$ の最後の出力ワイヤーと、$`g`$ の最初の入力ワイヤーの色が一致

これ以外でも繋げるケースはありますが、繋げるかどうかはワイヤーの本数に依存してしまいます。上記のそれぞれの場合のナロー多結合を次のように書くことにします。

  1. $`f \mathop{_1;_p} g`$
  2. $`f \mathop{_m;_1} g`$

ワイヤーの束を多結合できるときがワイド多結合〈wide polycomposition〉です。ワイヤーのk本の束を表すために、次の記号を使います。

$`\quad 1..k := \{ x\in {\bf N}\mid 1\le x \le k\}`$

この記法を使ってワイド多結合を次のように書くことにします。繋ぐワイヤー達の色は揃っている必要があります。

  1. $`f \mathop{_{1..k};_{(p - k + 1)..p}} g`$
  2. $`f \mathop{_{(m-k + 1)..m};_{1..k}} g`$

これ以外の多結合可能パターンについては省略します。多結合に関する計算法則はかなり煩雑な形になるので、これも割愛します。述語論理のために使う多圏は、対称モノイド圏から構成したもので、それ自体が対称モノイド圏になるので、煩雑な計算法則は実は不要です。

ここまで、色と色リスト〈list of colors〉を表す文字を区別しませんでしたが、色をラテン文字、色リストをギリシャ文字 $`\Gamma, \Delta`$ などで表すこと（シーケント計算風記法）が多いようです。

色々な多圏の呼び名

ワイヤリング規律による分類をそのまま形容詞にすると、2×2×2 = 8 種類の多圏が生じます。

  1. 非対称・非モノイド・ナロー多圏
  2. 非対称・非モノイド・ワイド多圏
  3. 非対称・モノイド・ナロー多圏
  4. 非対称・モノイド・ワイド多圏
  5. 対称・非モノイド・ナロー多圏
  6. 対称・非モノイド・ワイド多圏
  7. 対称・モノイド・ナロー多圏
  8. 対称・モノイド・ワイド多圏

長たらしいので省略しようとすると問題が生じます。例えば、「非モノイド・ワイド多圏」と言うと、対称性に関して次の可能性があります。

  1. 非対称・非モノイド・ワイド多圏
  2. 対称・非モノイド・ワイド多圏
  3. 非対称・非モノイド・ワイド多圏と対称・非モノイド・ワイド多圏の総称

短縮して呼びたいときは、その場その場で短縮のルールを決めることにしましょう。（ルールや定義が明示されないで単に「多圏」と言われても意味不明で困ります。）

色〈単純対象〉の集合が単元かどうかで、色なし〈uncolored〉／色付き〈colored〉という形容詞を使うことがありますが、ここでは使いません。色の集合が単元集合なら、単一色〈single colored | 単色〉を付けるだけです。

特定の種類の多圏には別名があります。

  1. 両オペラッド〈dioperad〉 ＝ 対称・非モノイド・ナロー多圏
  2. プロペラッド〈properad〉 ＝ 対称・非モノイド・ワイド多圏
  3. プロップ〈PROP〉 ＝ 対称・モノイド・ワイド多圏

述語論理のために使う多圏はモノイド構造があるので、次の4種です。

  1. 非対称・モノイド・ナロー多圏
  2. 非対称・モノイド・ワイド多圏
  3. 対称・モノイド・ナロー多圏
  4. 対称・モノイド・ワイド多圏

これらについては、呼び名の短縮のルール（形容詞のデフォルト・ルール）を決めておきます。

  1. 非対象／対称 の省略時〈デフォルト〉は非対称
  2. ワイド／ナローの省略時〈デフォルト〉はワイド

したがって、

  1. モノイド多圏〈monoidal polycategory〉 ＝ 非対称・モノイド・ワイド多圏
  2. 対称モノイド多圏〈symmetric monoidal polycategory〉 ＝ 対称・モノイド・ワイド多圏 ＝ プロップ

後で述語論理で使う多圏は対称モノイド多圏であり、対称モノイド圏から構成されたものに限ります。

まとめ

述語論理の道具として使う多圏は、モノイド多圏／対称モノイド多圏だけです。一般的（構造・性質が少ない場合の）煩雑な計算法則は必要ありません。モノイド圏に加えて次の用語・概念があれば十分です。

  1. 色 ＝ 単純対象
  2. 色リスト
  3. 多射
  4. (n→m)-多射
  5. 多ホムセット
  6. 多結合（ナロー多結合、ワイド多結合）
  7. 多圏の対称構造（対称群によるワイヤー入れ替え）
  8. 多圏のモノイド構造（横に並べる操作）

*1:「対称モノイド多圏（簡約版）」では、単純対象を分子〈molecule〉と呼んでました。