ボックス&ワイヤー図、あるいはストリング図において、ワイヤー(ストリング)の並置はモノイド積を表します。モノイド積が2種類、例えば×と+があると、単に並置するだけではどっちの積か分かりません。そこで、ワイヤー間の帯状領域に色を塗って区別することにします。例えば、×が赤、+が青とか、3色ペンの出番ですぜ。
また、A, B, C 3本のワイヤーがあるとき、「AとB」、「BとC」のどちらを先に演算するかを示すために、束ね糸を使うことにします。このお絵描き方式で分配律を描くと次のようです。
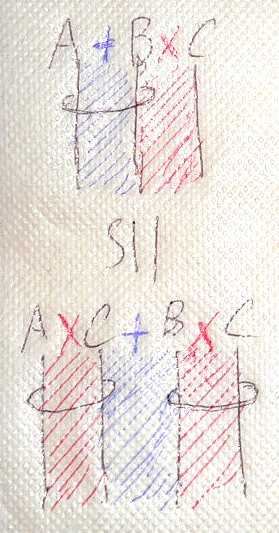
分配律は、形状を完全に描き換える必要があって、絵算的には厄介なことになってしまいます。残念ながら、分配律を含む計算は平面絵算には向きません。しかし、次ならどうでしょう。これなら、形状の変化がないので、絵算的には何の操作も要らなくて大変にありがたい。
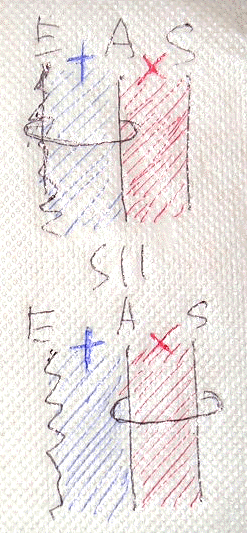
このありがたい法則が分合律*1 (E+A)×S = E+(A×S) です*2。Eのワイヤーを波線で描いたのは、Eは例外のデータ型(例外クラス)だからです。演算+は、例外データ型を左に、通常データ型を右に置く足し算で、普通の足し算(直和)と完全に同じではありませんが、ほとんど普通の足し算として扱えます。
色と分合律を使って、状態参照と例外を含む計算のクライスリ結合を描いてみると次のようです。モノイド積の種類は色で区別できますが、センター(メインストリーム入出力)より右側が直積、左側が直和になるように描いてあります。
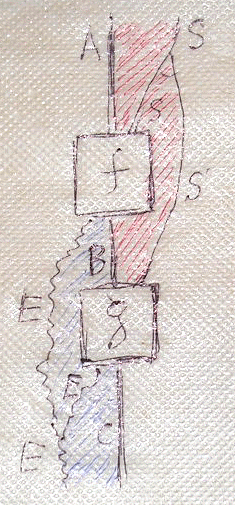
対称性を持ったきれいな図形です(僕の絵はキタネーけど)。この対称性は、「直和⇔直積」の双対性と、「対角コモノイド⇔余対角モノイド」の双対性に起因します。つまり、この絵は状態参照と例外生成の双対性を如実にかつ印象的に表しているのです。
上で、「クライスリ結合」と書きましたが、実際は一般化されたクライスリ結合です。この結合に対する恒等を定義して、一般化されたクライスリ圏(一般化クライスリ圏)がほんとに圏になるのを確かめるのは良い練習問題です。
僕は、クライスリ結合とその周辺をもっと一般化して、もっと不純な計算まで扱えるようにしたいのですよ。大域脱出とか、自分を書き換えるコードとか。