「交替律と分合律」にて:
ストレージIOを含む例外付き計算の一般化クライスリ圏が、イミュータブルな場合の自然な拡張として作れるはずです。作れたらいいな … 。
たぶん出来たような気がする。一番簡単な場合のクライスリ射は次のような感じ。
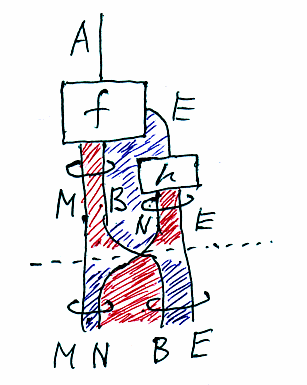
A, B, E は集合圏Setの対象で、M, Nはモノイドの圏(モノイド圏ではない)Monの対象。ほんとは、SetとMonを分離して扱わないとマズイですが、面倒なのでMonがSetの部分圏のような言い方をします。
E, M, N は一時的に固定します。E, M, N をインデックス付き圏のベースとして動かせば、任意の E, M, N を扱えますが、とりあえずは局所的な話(つまり、ひとつのファイバーだけを見る)。
f: A → (M:×B) +: E と書いたら、「:×」は直積で「+:」は直和ですが、「:×」の左は作用を表現するモノイド、「+:」の右側は例外の型だと解釈します。ですが、こんな記号は覚えにくいので、自然言語風の次の記法も使います。
f requires A as input (returns B as output and posts M as effect ) or throws E as exception
上の図のhは例外ハンドラーで、例外時の処理として型Nのデータを作用キューにポストしてから例外を再スローするとします。この例外ハンドラーhはプログラマが書くのではなくて勝手に付加されるものです。fとhをまとめた処理をgとすると、その仕様(プロファイル)は次のように書けます。
g requires A as input (returns B as output and posts M as effect ) or (throws E as exception and posts N as effect )
さらに、交替律を使って and と or を入れ替えると次のようになります。
k requires A as input (returns B as output or throws E as exception ) and posts (M or N) as effect
kは、fから一意的に決まります。例外のあるなしに関わらず、作用は必ずキューにポストされます。Mが正常時の作用、Nが異常時(例外が起きたとき)の作用です。M or N はモノイドの直和(自由積です)を意味します。Nが単位だけの自明なモノイドなら、M or N はM と同じです。このときは、例外なら何もしないこと(モノイド単位の作用)になります。
以上のようにして作ったkがクライスリ射です。つまり、SetとMonが混じったような圏のなかで、k : A → (M + N)×(B +:E) があると、それはクライス圏Kの射 f: A→B in K を定義します。クライスリ射の結合は少し面倒ですが、普通にやれば定義できます。
今の例は、作用モナドと例外モナドを交替律で組み合わせましたが、実際はとある双モナド*1と例外モナドと組み合わせるのでもう少し複雑になります。が、ややこしくなる以外の困難はないように思われます(交替律の厳密な定式化はけっこう手間がかかりそうですが)。
[追記]
M or N はモノイドの直和(自由積です)を意味します。
直和だというのはオカシイかもしれない。だけど、
Nが単位だけの自明なモノイドなら、M or N はM と同じです。このときは、例外なら何もしないこと(モノイド単位の作用)になります。
この結果は変わらないので、当面の目的には影響しないです。
もともと、「交替律」という言葉は便宜的で、表層的な形が似ているのでそう呼んでましたが、内容的にはだいぶ違うのかもしれません。
(交替律の厳密な定式化はけっこう手間がかかりそうですが)。
試行錯誤の結果として表層的な形はだいたいわかるんですが、メカニズムが完全には分かってないです。
[/追記]
[さらに追記]
表層的な形はだいたいわかるんですが、メカニズムが完全には分かってないです。
実装するには問題ない、うまくいきそうだ、という点では結果オーライだけど、どこかで何かがズレている。
疑わしいのは、例外処理がうまくいく事情が、交替律の類似とは別な事情かもしれないことですね。
[/さらに追記]
*1:双モナドよりもさらに複雑かも。