このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

メイヤー先生からモナド類似構造へ

雑記／備忘 檜山用メモ

「計算モデル： 大域と局所、不純と純粋」において、不純な局所計算モデルには「Command-Query分離された状態遷移系」を採用したいと書きました。Command-Query分離とは、あの偉大なメイヤー先生が提唱している原理です。ストレージIOなどは、メイヤー先生の教えに従ってやりたいのです。

「モノイドから得られるモナドを特徴付けるには？ （よくワカリマセン）」において、モナドFが、モノイドMによる掛け算関手（スタンピング関手）になっていることを判定できたらいいな、と書きました。モノイド閉圏で考えるなら、自己関手Fの随伴関手が内部ホム関手（自己豊饒化）の意味で表現可能なとき、Fが掛け算関手になっているようです。この問題を双対化して、コモナドGがコモノイドVの掛け算関手で表現されるかどうか？ を考えることもできます。

「ストレージの線形代数： 泥臭いデータ操作の洗練された定式化」では、ファイルシステムやデータベースに対する書き込み操作が、モノイドとその上の加群とみなせることを説明しました。

これらの話は実は関連していまして、メイヤー先生の「Command-Query分離された状態遷移系」を作用圏やフレイド圏の枠組みで使えないか、というのが問題意識です。メイヤー先生の「Command-Query分離された状態遷移系」に対応する代数構造を考えることができます*1。その代数構造を、基礎となる圏の自己関手圏に埋め込むことができます。すると、モナド類似物になります。モナド類似物はいっぱいあるので、そのなかで「Command-Query分離された状態遷移系」から作られたものを特定できるといいな、と思うのです。それができないにしても、メイヤー先生の教えを圏論的に考えるのは興味深い話です。

内容：

前提となること

まだなんだか曖昧模糊とした話なんですが、とりあえずは、メイヤー先生の「Command-Query分離された状態遷移系」に対応する代数系をスケッチしておきます。メイヤー代数とかメイヤー構造とか呼ぶことにします*2。

対称モノイド圏内のモノイド、余モノイド（コモノイド）、双モノイドの概念は前提とします。次の過去記事を参照してください。

モナドは自己関手圏のなかのモノイドとなります。この事については：

モノイドと余モノイドは双対な概念ですが、自己関手圏のなかの余モノイド（コモノイド）がコモナドです。もちろん、モナドとコモナドは双対な概念です。モナド／コモナドの双対性については：

一番簡単で一番重要なコモノイドは対角コモノイドです。対角コモノイドの掛け算関手によりコモナドが作れます。対角コモナドですね。メイヤー構造として使うコモノイド／コモナドは対角コモノイド／コモナドです。対角コモノイドは、物理や計算科学における観測の“古典性”を表現しているようです。

対称モノイド圏のなかのメイヤー代数

さて、メイヤー代数の定義をザッと述べましょう。以下、記号の乱用をして、台対象とその上の代数系に同じ記号を使う（意図的混同をしている）ので注意してください。

メイヤー代数は、群やモノイドのような単ソート代数ではなくて、ベクトル空間や加群のような多ソート代数です。背景となる対称モノイド圏Cのなかの2つの対象M, Vを取ります。気持ちとしては、MがCommand（更新操作）のモノイド、VがQuery（観測操作）のコモノイドを表します。MとVは無関係ではなく、ある法則により制約されて整合性を持ちます。

Mは、(M, e, m) というモノイド構造を持ちます。さらにMは、Commandの複製に相当する余モノイド構造を持ち、これは (M, !, Δ) とします。!が余単位、Δが余乗法（余積）です。!, Δ は対角コモノイドを意識した記号ですね。全体として (M, e, m, !, Δ) は双モノイドとなっています。つまり、次の図で表される双代数法則（双モノイド法則）を満たします。（より詳しくは「ホップ代数の法則達の絵」）

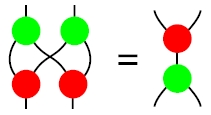
今後Mは双モノイドと考えますが、Mのモノイド部分に注目するときは、Mmon と書くことにします。Mmon は、双モノイドMに、コモノイド構造を忘れる忘却関手を作用させたものです。

もうひとつVという代数系を考えます。こちらは余モノイドです。V = (V, !, Δ) と書きましょう。同じ記号 !, Δ を使ってますが、これはV上の余単位と余乗法です。余モノイドVの余モノイド構造を忘れてCの対象とみなしたものを Vobj と書きます。

双モノイドMと余モノイドVの組み合わせがメイヤー代数となるには、さらに次の構造と法則が追加されます。

  1. VobjがMmon上の加群となるように、スカラー乗法 a:V×M→V in C が与えられている。
  2. スカラー乗法aに関する双代数法則が成立する。

aが右乗法の形になってますが、左乗法でもかまいません。VがM上の片側加群になっていれば左右は問いません（ただし、どっちかに固定する）。

スカラー乗法aに関する双代数法則とは次の法則です。×はCのモノイド積、Iはモノイド単位対象、σは対称、iは I×I→I の同型とします。

  1. a;Δ = (Δ×Δ);(id×σ×id);(a×a)
  2. a;! = (!×!);i

二番目は、「データを捨ててしまうなら事前に何をやっても関係ない」といった内容で、特に問題なく成立します（たいていは）。一番目はけっこう実現が難しい条件で、Commandによる更新で「Queryによる観測結果」がどう変わるかを事前に予測可能であることを主張しています。「リモートストレージへの変更を、ローカルキャッシュ上で完全にシミュレートできる」ということです。

自己関手上のメイヤー構造

対称モノイド圏C内のメイヤー代数の構成要素は次のようになります。

  1. 対象M
  2. 単位 e:I→M
  3. 乗法 m:M×M→M
  4. 余単位 !:M→I
  5. 余乗法 Δ:M→M×M
  6. 対象V
  7. 余単位 !:V→I
  8. 余乗法 Δ:V→V×V
  9. スカラー乗法（作用） a:V×M→V

同じ記号を使ってますが、余単位、余乗法は2つずつあります。法則性としては、Mが双モノイド、Vが余モノイド（コモノイド）、スカラー乗法aによりVがM右加群、そしてaに関する双代数法則です。これらの法則は圏の可換図式を使って記述できるので、メイヤー代数の概念は任意の対称モノイド圏の上で定義可能です。

では、圏Cの自己関手の圏 E := End(C) の上でメイヤー代数を定義可能でしょうか？ 残念ながらそのままではうまくいきません。圏Eには対称性がないので、双代数法則が記述できないのです。よって、「Mが双モノイドであること」や「aに関する双代数法則」などが意味を持ちません。

モノイド圏の対称性σは、圏全体に渡って大域的に定義された自然変換（同値） σX,Y:X×Y→Y×X です。非対象なモノイド圏では、そのような大域的な自然変換は取れません。しかし、個別のX、Yを取ったとき、XとYをスワップする自然変換 X×Y→Y×X なら選べる可能性があります。つまり、対称性を圏全体の構造として持つのではなくて、個々の代数系ごとの局所的／個別的な対称性として定義します。

局所対称性を定義に含めると、先の構成要素に加えて、M×M→M×M と V×M→M×V というスワップ射が増えて、これを使って双代数法則を記述します。この方法を使って、E内のメイヤー代数＝自己関手上のメイヤー構造を定義できます。その構成要素は次のようになります。

  1. 自己関手 F:C→C
  2. 単位自然変換 η:Id⇒F
  3. 乗法自然変換 μ:FF⇒F
  4. 余単位自然変換 ε:F⇒Id
  5. 余乗法自然変換 δ:F⇒FF
  6. スワップ自然変換 γ：FF⇒FF
  7. 自己関手 G:C→C
  8. 余単位自然変換 ε:G⇒Id
  9. 余乗法自然変換 δ:G⇒GG
  10. スカラー乗法（作用）自然変換 α:GF⇒G
  11. スワップ自然変換 β:GF⇒FG

スワップ自然変換 γ：FF⇒FF を使うことにより、Fが双モナド（圏E内の双モノイド）であることを記述できます。β：GF⇒FG を使うと、αに関する双代数法則を記述できます。γやβは、ベックの法則の公理を満たすことを要求します。

これで、非対称モノイド圏E（= End(C)）内のメイヤー代数が定義できます。複雑そうですか？ ストレージ操作のモデルを作ろうと思うとまーコンナモンですよ、そんなに簡単にはできないんです。

ベースとなる圏C内のメイヤー代数(M, V)があれば、F(X) := X×M、G(X) = X×V として、その他諸々の自然変換を定義すれば、2つの自己関手F, Gを台とするメイヤー構造を構成できます。この構成は、圏C内のメイヤー代数の圏（ちゃんと定義してませんが）から圏E内のメイヤー代数の圏への埋め込みとなるものです。圏CをSetのような具体的な圏に取れば、メイヤー代数と「Command-Query分離された状態遷移系」（のクライアント部分）は事実上同じものなので、自己関手上のメイヤー構造の例はすぐに作れます。

メイヤー代数上の加群とアイレンベルク／ムーア圏

圏C上のモナド F = (F, η, μ) が、圏C内のモノイドMを使って F(X) := X×M と（関手の同値の意味で）書けるとき、モナドFの代数 a:F(A)→A in C は、a: A×M→A なので、M右加群となります。加群の左右は気にしないことにして、単にM加群と呼びましょう。

モナドFに対するF代数の圏 Alg(F) はアイレンベルク／ムーア圏に他なりません。一方で、モノイドMに対する加群の圏 Module(M) は、モナドに言及せずに構成できます。F(X) := X×M のとき、この2つの圏 Alg(F) と Module(M) は圏同値になります。

以上の事実と同じことがメイヤー代数に関しても成立しているように思えます。自己関手の対(F, G)上のメイヤー構造はモナド類似物（monad-like entity）であり、アイレンベルク／ムーア構成と類似の方法が使えそうです。メイヤー代数(M, V)上の加群はハッキリ定義できるので、加群の圏 Module(M, V) を構成できます。メイヤー構造を持つモナド類似物のアイレンベルク／ムーア類似圏は、メイヤー代数上の加群の圏とたぶん圏同値でしょう。

圏C内のメイヤー代数より、非対称モノイド圏E（= End(C)）に持ち上げたメイヤー構造を考えたいのは、モナドの相対化やインデックス付け（パラメトライズ）と似たことをメイヤー構造に対しても行えるとうれしいからです。

ストレージのクライアント／サーバー・モデル

不純な計算のなかで実務上一番よく使うのはおそらく副作用（主作用？）で、副作用のなかで最も重要なのはストレージIOでしょう。

ストレージサービスが、サーバーとクライアントで与えられるとして、キャッシュ付きのクライアントの定式化がメイヤー代数です。クライアントとサーバーを一緒に考えると加群の構造を持ちます（この事情の背景は「ストレージの線形代数： 泥臭いデータ操作の洗練された定式化」参照）。メイヤー代数の定義に含まれる双代数法則は、クライアント側キャッシュの整合性の条件です。

Command-Query分離された状態遷移系、メイヤー代数、自己関手上のメイヤー構造、メイヤー代数上の加群などの関係がハッキリすれば、トランザクションや排他制御の話を含めて*3ストレージの扱い方がもう少しわかるんじゃないかなー、と期待してます。いまのところ、期待に過ぎませんが。

*1:実際は、インターフェースと実装、クライアントとサーバーなどにより、何種類かの代数構造が出現します。

*2:メイヤー代数／メイヤー構造は、状態遷移系のインターフェース部／クライアント部の定式化です。

*3:ひとつのモノイド（多元環）上のたくさんの加群を考えるのは普通ですが、ひとつの加群（の台）にたくさんのモノイドを考えることはあまりしません。せいぜい2つのモノイド作用を持つ両側加群（双加群）くらいです。トランザクションや排他制御の話が代数化しにくいのは、多数のモノイドが作用する加群の議論が不足しているせいかもしれません。