「あわてて両モナドやメイヤー代数を復習する」と「メイヤー代数/メイヤー加群の定義を仕切り直す」において、以前に定義したメイヤー代数/メイヤー加群の定義はキツすぎると言いました。ですが、当時キツい定義を採用したのはそれなりの理由があってのこと。どうも、後になってその状況を忘れてしまったようです。
最初の定義で、双代数の条件を入れておいたのはトランザクションのためでした。トランザクションは、「更新オペレータをローカルでキューイングする」方式を前提とします。Sが状態空間、Mが状態空間に作用するモノイド、Vが状態を観測した値の空間だとして、トランザクションのためには次のような同型が要求されます。
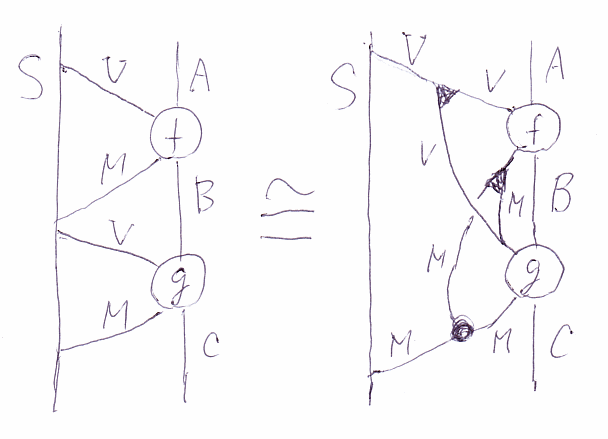
ここで、黒三角はVとMの余モノイド余乗法、黒丸はMのモノイド乗法、他のワイヤー交点は作用と余作用です。
双代数の法則は絵で描けば(バエズによる図示):
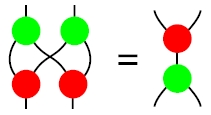
これは対称性がありますが、メイヤー加群では非対称になります。下の図で、(1)から(2)に変形するとき、(1)の赤い点線内を(2)の赤い点線内に置き換えるときに使っているのが双代数の法則の類似物です。これを使えば、冒頭の同型は示せます。
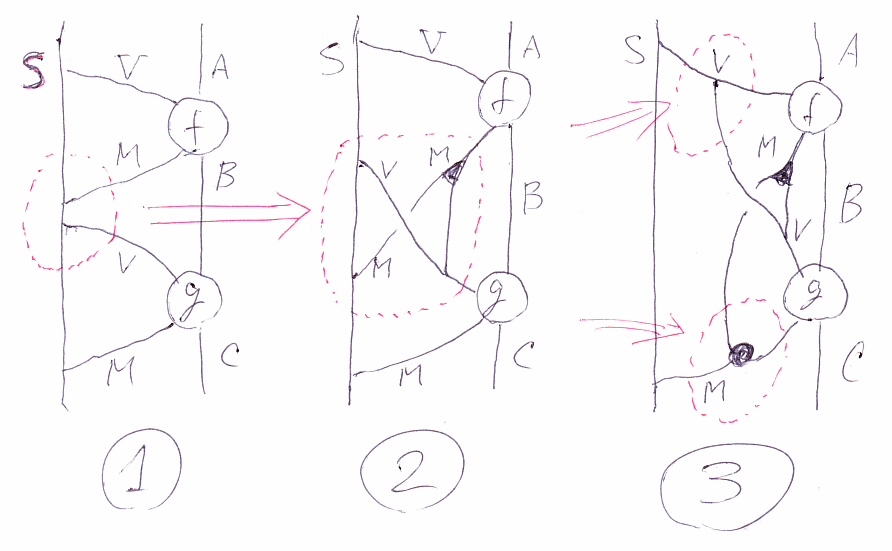
(2)から(3)に行くときは、余モノイドの余結合律とモノイドの結合律を使っています。
トランザクションの文脈では、キツい法則性も必要だったのです。トランザクションが不要なら(あるいは別な方式のトランザクションなら)条件をゆるめることが出来るでしょう。どんな状況で、どんな法則性が必要か、もう少し整理する必要がありますね。