トレースのタイトニングが自然変換であること

以下の絵は、新しいスタイルのトレース付き圏（トレース付きバランス圏とその特殊化）の公理を表しています。（長谷川真人さんの "On Traced Monoidal Closed Categories", 28 November 2007 より、「トレース付きモノイド圏の新しい定義」から再掲。）

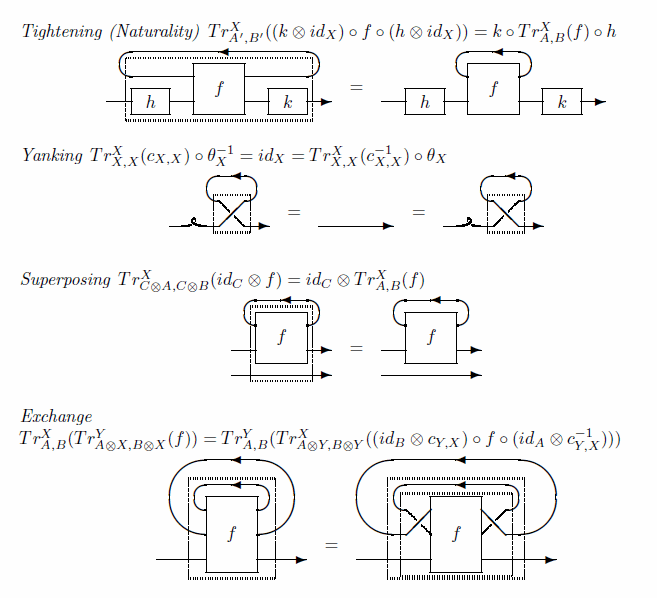
ここで、タイトニング（Tightening）が自然性（Naturality）とも呼ばれています。これは、トレースが自然変換の性質を持つことですが、毎回「どこが自然なんだっけ？」と忘れてしまいます。なので、ここにメモしておきます。

---

子供が小さい頃、世田谷公園は良い遊び場でした。上の子（兄）がある程度大きくなってからは、兄弟で遊んでいるあいだ、僕はベンチに座って本や書類を読んだりしていても大丈夫でした。「タイトニングのどこが自然なんだ？」は、世田谷公園のベンチで考えた記憶があります。

（画像は http://www.asobi-map.com/setagaya.htm より）

---

先の絵だと、左右のタイトニングが一度に表現されていますが、左タイトニングだけだと次のようになります。（図式順記法に変えてあります。）

• Tr_A',B^X((h×X);f) = h;Tr_A,B^X(f)

この等式がなんらかの自然変換の自然性になっているはずです。

A, B, X を圏Cの対象として、トレースは、C(A×X, B×X)→C(A, B) というホムセットのあいだの写像として与えられます。ここで、B, X を固定して、Aだけを動かすとします。
すると、h:A'→A という射に対して、C(A×X, B×X)→C(A'×X, B×X) が、(f:A×X→B×X) |→ (h;f:A'×X→B×X) として定義できます。この定義により、C(-×X, B×X) は C→Set という反変関手となります。反変ホム関手の変形版ですね。

さて、Tr_A,B^X を（自然変換らしく） τ_A と書きましょう。先の左タイトニングの等式は、次のように書き換えることができます。

• τ_A((h×X);f) = h;τ_A(f)

変数fを消して簡略化すると：

• (h×X)^*;τ_A = τ_A;h^* : C(A×X, B×X)→C(A', B)

可換図式にするなら：

C(A×X, B×X) -(τA)--> C(A, B)
   |                      |
  (h×X)*                 h*
   |                      |
   v                      v
C(A'×X, B×X) -(τA')-> C(A', B)

τは、変形版反変ホム関手 C(-×X, B×X) と普通の反変ホム関手 C(-, B) のあいだの自然変換です。

[追記]

Aをパラメータ域とするパラメータ付き不動点演算子は、Fix_A^X:C(A×X, X)→C(A, X) というホムセットのあいだの写像として与えられます。不動点演算子Fixでも、タイトニングとよく似た等式が成立しますが、これも自然性です。

問題の等式は、f:A×X→X、h:A'→A として、Fix_A'^X((h×X);f) = h;Fix_A^X(f) の形です。これは、φ_A = Fix_A^X と置いて、(h×X)^*;φ_A' = φ_A;h^* と書けます。可換図式では：

C(A×X, X) -(φA)--> C(A, X)
   |                    |
  (h×X)*               h*
   |                    |
   v                    v
C(A'×X, X) -(φA')-> C(A', X)

φも、変形版反変ホム関手 C(-×X, X) と普通の反変ホム関手 C(-, X) のあいだの自然変換です。

[/追記]