不動点理論と対角自然性（dinaturality）

土曜日（2013-09-28）に書いた「トレースのタイトニングが自然変換であること」において、トレースのタイトニング公式と不動点に関するタイトニング類似の公式が、ある自然変換の自然性（naturality）の記述であることを示しました。

不動点演算子の公理には、もうひとつ「対角自然性（dinaturality）」と呼ばれる等式があります。自然性が自然変換の定義であるのと同様に、対角自然性は対角自然変換（dinatural transformation）の定義となります。

不動点演算子の対角自然性も、実際に対角自然変換が存在することを主張するのだろう、と思っていました。確認してみると、だいたいそうなっているようです。ところが、いつも「だいたい」で、最後の詰めがうまくいきません。本来の対角自然性から少しズレちゃうんですよね。

結局、バッチリと対角自然変換を作れたタメシがないのですが、自分がなんか勘違いか計算違いをしているのだろう、という程度に考えてウヤムヤに済ませてきました。で、土曜日に再度計算してみたのですが、やっぱりうまくいかない。「ほんとに対角自然変換なのか？」と疑わしくなってきました。そのことについて書きます。

不動点理論の舞台

Cがデカルト圏であるとき、対角 Δ_A:A→A×A と終対象への唯一射 !:A→1 によって、任意の対象Aは、余モノイド構造 (A, Δ, !) を持ちます。余モノイドと考えたAを X→Y の域側に直積スタンピングすると、射は f:A×X→Y の形になります。この操作は余モナド（コモナド）になります。余モノイドAを域側に掛け算する余モナドによる余クライスリ圏を C^A とします*1。定義より、集合としては C^A(X, Y) = C(A×X, Y) です。

射 σ:A→B があると、C^B→C^A という関手が (σ×X)^*:C^B(X, Y)→C^A(X, Y) の形で定義できます。関手性は、Δの性質 σ;Δ = Δ;(σ×σ) から出ます。このことから、A |→ C^A という対応は関手性を持ち、全体として C^op→Cat という関手、つまりインデックス付き圏となります。このインデックス付き圏を C[-] = C^- と書くことにします。

任意のAに対して |C[A]| = |C| であり、σ:A→B に対する関手 C[σ]:C[B]→C[A] は、identity-on-objects な関手です。C[1] は C と同型（同一視可能）で、A→1 の唯一射から誘導される関手 (C = C[1])→C[A] があります。これを、J_A:C→C[A] とすると、フレイド圏 (C, C[A], J_A) がパラメータAによって束になっているような状況となります。

以上にようにしてデカルト圏Cから作られたインデックス付き圏 C[-] が、不動点理論を展開するのにふさわしい舞台なんじゃないかと思います。

自己プロ関手と対角自然変換

一般に、C^op×D→Set という混合変性（反変-共変）の二変項関手をプロ関手（profunctor）と呼びます。distributor、correspondence、bimodule あるいは単に module と呼ばれることもあります。値の圏をSet以外にすることもありますが、ここではSetに固定します。

C = D のときのプロ関手、つまり C^op×C→Set の形の二変項関手を自己プロ関手と呼びます。雰囲気的／感覚的に言えば、自己プロ関手は、集合値の正方行列のようなものです。圏C上の二変項ホム関手は、典型的な自己プロ関手です。FとGが圏C上の自己プロ関手のとき、FからGへの対角自然変換が定義できます。

自己プロ関手FからGへの対角自然変換αは、自然変換と同様に対象で添字付けられた射の族ですが、二変項関手の対角部分でしか定義されていません。つまり、

• α_X:F(X, X)→G(X, X) in Set （X∈|C|）

対角自然変換αは、六角形の可換図式を満たします。その図式は、例えば http://en.wikipedia.org/wiki/Dinatural_transformation に載っています。より詳しくは http://ncatlab.org/nlab/show/dinatural+transformation などを参照してください。

さて、不動点演算子に関わる対角自然変換ですが、対角自然変換というからには次の4つの構成要素が必要です。

1. 定義域となる圏
2. 1つ目のプロ関手
3. 2つ目のプロ関手
4. 圏の対象で添字付けらた写像（集合圏の射）の族

定義域となる圏は、デカルト圏Cに対する余クライスリ圏C^A（Aをいろいろ動かす）で良さそうです。1つ目のプロ関手は、圏C^A 上の二変項ホム関手 (X, Y) |→ C^A(X, Y) が適切です。

問題は2つ目のプロ関手で、これがうまく見つからないのです。毎度ここで行き詰まります。

変形された対角自然変換

ここからの話は、いちおう辻褄は合っていると思いますが、僕が何か勘違いをしている可能性もあります。なかなかうまく行かないので、変換の定義を少し変更してみる話です。

対角自然変換は、2つのプロ関手のあいだの変換ですが、プロ関手と通常の関手のあいだの変換を考えます。次のようなセッティングとなります。CではなくてDと書いているのは、後で使う記号とかち合わないようにです。

1. Dは圏である。
2. F:D^op×D→Setは、D上の自己プロ関手である。
3. G:D→Setは、D上の（普通の）共変関手である。
4. αは、α_X:F(X, X)→G(X) in Set という、Dの対象で添字付けられた写像の族である。

αが満たすべき条件は六角形ではなくて五角形の可換図式（下の図）となります。その五角形図式から得られる等式を、次のように具体化します。

1. Dとして、C^A を取る。
2. 自己プロ関手Fとして、二変項ホム関手 (X, Y) |→ C^A(X, Y) を取る。
3. 関手Gとして、共変一変項ホム関手 X |→ C^A(1, X) を取る。
4. 変換の成分 α_X:F(X, X)→G(X) として、不動点演算子 Fix_A^X:C^A(X, X)→C^A(1, X) を取る。

この具体化を、可換図式と絵を混ぜて描いたのが次です。赤い絵では、Aも描いているので、C^A の射を、Cにおけるイメージで表現していることになります。

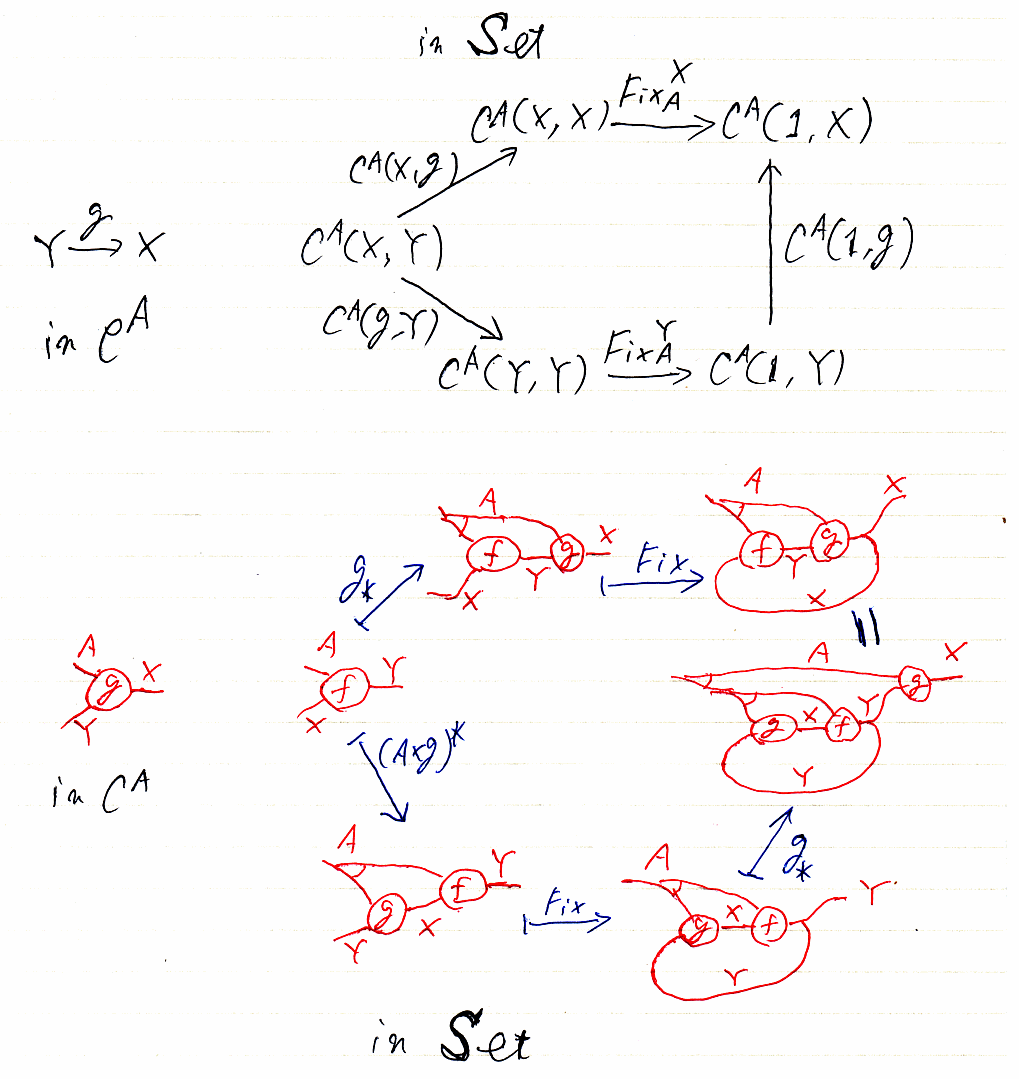
不動点の対角自然性は Composition Identity と呼ぶことがありますが、次のように考えるとこの呼び名はふさわしいと思えます； C^Aは余モナドの余クライスリ圏ですが、そこでの結合を記号「#」表すと f#g = Δ_A;(A×f);g と書けます。不動点演算子を (-)^† と書くと、次の等式が得られます。

• (f#g)^† = (g#f)^†#g

C^A での結合に対する不動点演算子が、逆順の結合を使って書き表せることになります。これは簡単な形をしているので、等式としても使いやすいでしょう。

六角形ではなくて五角形の可換図式で表現される“対角自然変換”が他に出てくるかどうか僕は知りませんが、どうやら余クライスリ圏の上のオペレーターをうまく記述しているようなので、他にも利用価値があるのかも知れません。

*1:クライスリ圏を C_A と書くことがあるので C^A としたのですが、アイレンベルク／ムーア圏も C^A のような書き方をするので、注意が必要ですね。