ずっと気になっていたことなのでメモしておきます、小ネタだけど。
内容:
モノイド閉圏とカリー化
最初に、モノイド閉圏とカリー化の話題を扱った過去記事へのリンクを示します。
絵の描き方については、上記の2つの記事を参照してください。モノイド積や指数の記号法が安定しない事情は次の記事に書いてあります。
さて、(C, , I, α, λ, ρ)をモノイド圏とします。いつもの記号の乱用で、C = (C,
, I, α, λ, ρ) とも書きます。
対象 A∈|C| を固定して、対象のあいだの対応: X|→AX、射のあいだの対応: f|→idA
f で決まる関手 C→C を、(A
-)、あるいは単に(A
)と書きます。(A
)は、モノイド積の意味での左からの掛け算関手です。関手 (A
):C→C に右随伴関手があるとします。(掛け算の左右と随伴の左右は別な話で関係はありません。)
- C(A
X, Y)
C(X, R(Y))
このとき、(A)の右随伴関手Rは対象Aから決まるので、R(-) = (A▷-) とします。つまり、
- R(Y) = (A▷-)(Y) = A▷Y
たまたまうまく選んだAではなくて、Cのすべての対象Aに対して(A)の右随伴があるとしましょう。
- A∈|C| ごとに、C(A
X, Y)
C(X, A▷Y)
- A∈|C| ごとに、(A
) -| (A▷)
(A▷-)を単に(A▷)と書いています。Aを固定して Y|→A▷Y は定義より関手ですが、(A, Y)|→A▷Y は二項関手 Cop×C→C となります。変数Aに関しては反変となることに注意してください。
今述べたような二項関手 (-▷-):Cop×C→C を指数関手〈{exponent | exponential | exponentiation} functor〉、または内部ホム〈internal hom〉と呼びます。
最近まで、指数/内部ホムはモノイド積があるから定義できるのだと僕は思っていたのですが、モノイド積がない状況でも指数/内部ホムは定義(公理化)できるようです。そのことは、次のnLabエントリーを参照。
モノイド圏Cが指数関手(内部ホム)を持つとき、Cをモノイド閉圏〈monoidal closed category〉と呼び、C = (C, , I, α, λ, ρ, ▷, Λ) と書きます。▷は指数関手です。Λは、(A
)と(A▷)の随伴においてホムセットの同型を与える写像です。Λは3つのインデックスを持ちます。
- ΛAX,Y:C(A
X, Y)→C(X, A▷Y)
ラムダ計算の用語法を使って、Λをカリー化〈currying〉と呼びます。Λは、ホムセットのあいだの写像として可逆なので、(ホムセットごとに)逆写像Λ-1を持ちます。Λ-1は反カリー化〈uncurring〉です。
左指数と右指数
前節の定義では、左からの掛け算(A)の右随伴を(A▷)と表しました。では、右からの掛け算(
A)の右随伴はどうでしょう。モノイド積
が対称でないときは、(A
)の右随伴があっても(
A)の右随伴の存在が保証されません。右からの掛け算(
A)の右随伴(それがあるとして)は、(◁A)とします。
- A∈|C| ごとに、C(X
A, B)
C(X, B◁A)
- A∈|C| ごとに、(
A) -| (◁A)
前節の(A▷)は左指数〈left exponentiation〉、(◁A)は右指数〈left exponentiation〉と呼びましょう。カリー化でも左右の区別をします。
- A∈|C| ごとに、lΛAX,Y:C(A
X, Y)→C(X, A▷Y)
- A∈|C| ごとに、rΛAX,Y:C(X
A, Y)→C(X, Y◁A)
lΛが左カリー化〈left currying〉、rΛが右カリー化〈right currying〉です。反カリー化についても同様です。
非対称なモノイド圏では、左指数と左カリー化を持つモノイド閉圏と、右指数と右カリー化を持つモノイド閉圏は区別すべきです。しかし、AB = B
A として新しいモノイド積
を定義すると、掛け算の左右がすっかり入れ替わるので、どちらか一方について考えればいいことにはなります。
対称な場合
モノイド閉圏で一番よく使うのはデカルト閉圏でしょう。デカルト閉圏のデカルト・モノイド積は対称です。対称な場合は、左右の区別に神経質になる必要はありません。そのため、指数やカリー化に関する左右をどうするかの自由度が増えて、むしろ混乱するのではないかと思います。このことが、「ずっと気になっていたこと」です。
対称モノイド圏の対称〈symmetry〉をσとします。
- σA,B:A
B→B
A
対称モノイド圏 C = (C, , I, α, λ, ρ, σ) が左指数▷と右指数◁の両方とも最初から持つとします。もちろん、左カリー化/左反カリー化、右カリー化/右反カリー化も持ちます*1。
- A∈|C| ごとに、lΛAX,Y:C(A
X, Y)→C(X, A▷Y)
- A∈|C| ごとに、rΛAX,Y:C(X
A, Y)→C(X, Y◁A)
これ以外にもカリー化の変種が存在します。次のように定義されるものです。
- rlΛAX,Y(f) := lΛAX,Y(σA,X;f) : C(X
A, Y)→C(X, A▷Y)
- lrΛAX,Y(f) := rΛAX,Y(σX,A;f) : C(A
X, Y)→C(X, Y◁A)
rlΛを絵で描けば次のようになります。
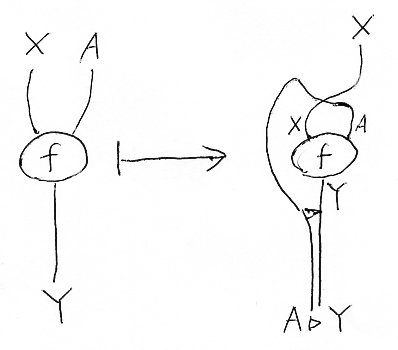
全部並べてみると:
- A∈|C| ごとに、lΛAX,Y:C(A
X, Y)→C(X, A▷Y)
- A∈|C| ごとに、rΛAX,Y:C(X
A, Y)→C(X, Y◁A)
- A∈|C| ごとに、rlΛAX,Y:C(X
A, Y)→C(X, A▷Y)
- A∈|C| ごとに、lrΛAX,Y:C(A
X, Y)→C(X, Y◁A)
2番目か3番目が使われているケースが多いように思います。しかし、左右の指数を区別しない(どちらか一方を単に指数とする)ので、使っている人がどちらを意図しているかは分かりません。複数ある指数とカリー化のどれを使っているかを明示しない/適当に混ぜる習慣は混乱を招くので良いとは思いません。
僕は、対称の場合でも左右の指数を区別する方針ですが、そのための適切な記法がないので苦労します。それが記号法が安定しない事情です。今回は、▷, ◁, lΛ, rΛ, rlΛ, lrΛ で区別しました。
*1:そもそも、カリー化/反カリー化(ホムセットの同型)の存在を前提として「指数」「内部ホム」という言葉を使います。