4月26日の記事「新しい絵算手法:ストリング+ストライプ図」を書いた時点で、例題である“結合律”を証明する絵〈pictorial proof〉は描いていました。翌日の「絵算のテキスト表現(結論:疲れる)」において、行列レイアウトを使って絵の一部をテキストに写し取ってみたのですが、疲れて途中でやめてしまいました。
4月30日の夜と5月1日の朝を使って、残りの写し取り作業を完成させたので、その結果をお見せしましょう。面倒だったよー。たぶん、こんな事はもうやらないと思います。
内容:
はじめに
なんで面倒な作業をやったのかというと; 典型的例題として提示した計算を途中でうっちゃっておく*1のもイカガナモノカ、という理由がひとつ。もうひとつ別な理由もあります。
絵算に関して、次のような印象を持つ人がいるかと思います。
- 人間の素朴な幾何的直感に頼っているので厳密性に欠ける。
- 絵図の操作は、公理化/アルゴリズム化が出来ない。
これらの疑念や不信がナンセンスであることを示すこともこの記事を書いた動機です。実際は、
- 人間の素朴な幾何的直感に頼っているのは事実だが、厳密性に欠けるわけではない。
- 絵図の操作を公理化/アルゴリズム化することは可能である。ただし、容易でないのは事実。
絵をテキストに翻訳してみれば、やっていることは記号的表現の等式的推論〈equational reasoning〉と同等なことだと分かるでしょう。
使ったテキスト表現手法は、「絵算のテキスト表現(結論:疲れる)」で紹介した行列レイアウトを使う方法です。これは、いわば苦肉の策です。苦肉の策でも無策よりはマシですが、いくつか問題があります。
行列レイアウトは、碁盤目状のグリッドレイアウトしか出来ません。絵算の絵は、碁盤目に区切るのが適切とは限りません。次の図は「絵算の威力をお見せしよう」で出したものです。
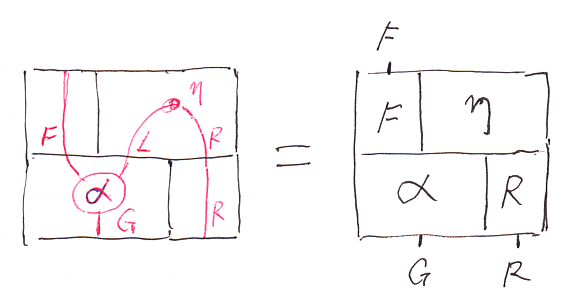
ご覧のように碁盤目ではない分割を使っています。仮に自由なレイアウトが出来ても、ワイヤーの繋がり具合という情報が見えなくなるので、テキスト化は劣化を伴います。
今回の等式的推論過程は、あくまで絵の写しと捉えてください。テキスト表現だけの計算としては無駄なところがあったりします。そもそも、テキスト表現だけで計算が出来るのか? というと、個人的には出来る気がしません。テキスト表現を見ても、どこをどう変形するかの方針が(僕には)立たないからです。しかし、計算過程をチェックする用途にはテキスト表現だけでも十分だと思います。
書き方のお約束
等式的推論とは、項をイコール記号で結んで変形していくことです。
項1 = 項2 : : = 項n
という形です。等式的推論しているんだ、って前提がハッキリしているなら、イコール記号は省略していいとします。
項1 項2 : : 項n
さらに、項の前後やあいだには説明(コメント)を入れます。説明文がどの項を説明しているかをハッキリさせるために次の約束をします。
- 直前の項に関する説明は、「//< 説明」と書く。
- 直後の項に関する説明は、「//> 説明」と書く。
- 直前の項から直後の項への変形を説明するときは、「//= 説明」と書く。
上記の約束でテキスト表現を記述します。絵はこの記事の後のほうに載せます。が、もともとは絵で、実質12ステップの変形で絵証明をしました。レイアウト変更(内容に変化なし)が3回あるので、絵図は16枚、レイアウト変更含めて15ステップです。先に絵を見たほうが分かりやすいかも知れません。
対応する項は全部で24項、計算は23ステップです。項が増えているのは、行列のレイアウト変更があるからです。
| no | 図番号 | 項番号 | no | 図番号 | 項番号 | no | 図番号 | 項番号 |
|---|---|---|---|---|---|---|---|---|
| 1 | 図1 | 項1 | 11 | 図6' | 項6' | 21 | 図11 | 項11 |
| 2 | 図2 | 項2 | 12 | 図6' | 項6'-A | 22 | 図12 | 項12 |
| 3 | 図2 | 項2-A | 13 | 図7 | 項7 | 23 | 図12 | 項12-A |
| 4 | 図2 | 項2-B | 14 | 図7 | 項7-A | 24 | 図13 | 項13 |
| 5 | 図2 | 項2-C | 15 | 図7 | 項7-B | 25 | 図13' | - |
| 6 | 図3 | 項3 | 16 | 図7 | 項7-C | |||
| 7 | 図4 | 項4 | 17 | 図8 | 項8 | |||
| 8 | 図4 | 項4-A | 18 | 図9 | 項9 | |||
| 9 | 図5 | 項5 | 19 | 図9' | 項9' | |||
| 10 | 図6 | 項6 | 20 | 図10 | 項10 |
定義
//< (def1)は明示的等号ノード〈explicit equality node〉として使う。
//< (def2)は置換〈substitution〉ルールとして使う。
ターゲット
//> 次が示すべきターゲットの等式。
項1から項6
//< (trm1)は結合律の左辺。
//= 4行目のmを(def2)により置換する。
//= レイアウト変更。
//= 入れ子をはずす。
//> ここで、マクロT1を定義する。
//= (mac1)を使って、(trm2-B)をマクロ縮約する。
//= テンソル強度を使って、左にあるmをFの内部に押し込む。
//= 右単位律子の作用点を上にズラす。
//> ここで、マクロT2を定義する。
//= (mac2)を使って、マクロ縮約する。
//= 一貫性と結合律子を使って、右単位律子の作用範囲を変更する。
//= テンソル強度をアンバンドルする。
項6'から項9'
//= マクロT2をマクロ展開する。
//> ここで、マクロT3を定義する。
//= (mac3)を使って、マクロ縮約する。
//= 3行目 F(m) のmを、(def2)により置換する。
//= レイアウト変更
//= Fを結合に対して分配する。
//= 入れ子をはずす。
//= 無駄な等号ノードを削除。
//= モナドの結合律により変形。
//= マクロT3をマクロ展開。
項10から項13
//= 右単位律子の作用点を下にさげる。
//= 余分な等号ノードを導入する。
//= N をくくり出す(モノイド積の共通因子)
//= (def2)により縮約する。
//< オシマイ
図の凡例
まず、絵図で使うアイコン(マーカー)を定義します。
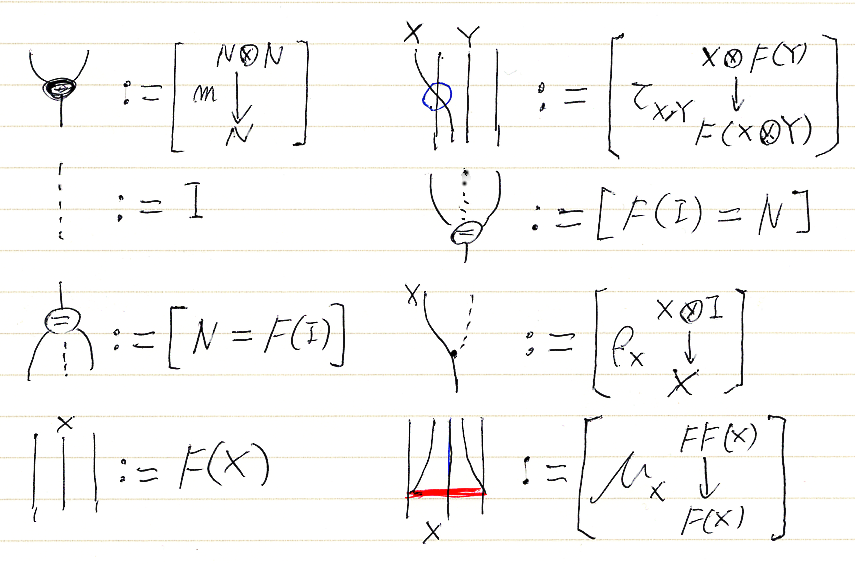
念の為:
- モノイドの乗法 m:N
N→N
- 圏の単位対象 I
- 名前の展開 N = F(I)
- 関手の値 F(X)
- テンソル強度 τX,Y:X
F(Y)→F(X
Y)
- 名前への縮約 F(I) = N
- 右単位律子 ρX:X
I→X
- モナド乗法 μX:FF(X)→F(X)
図1から図6
各変形ステップについては、項1から項6の説明(コメント)を参照してください。P1, P2は、描画を簡略化するために絵の一部に名前を付けたものです。項におけるマクロ定義に対応しています。
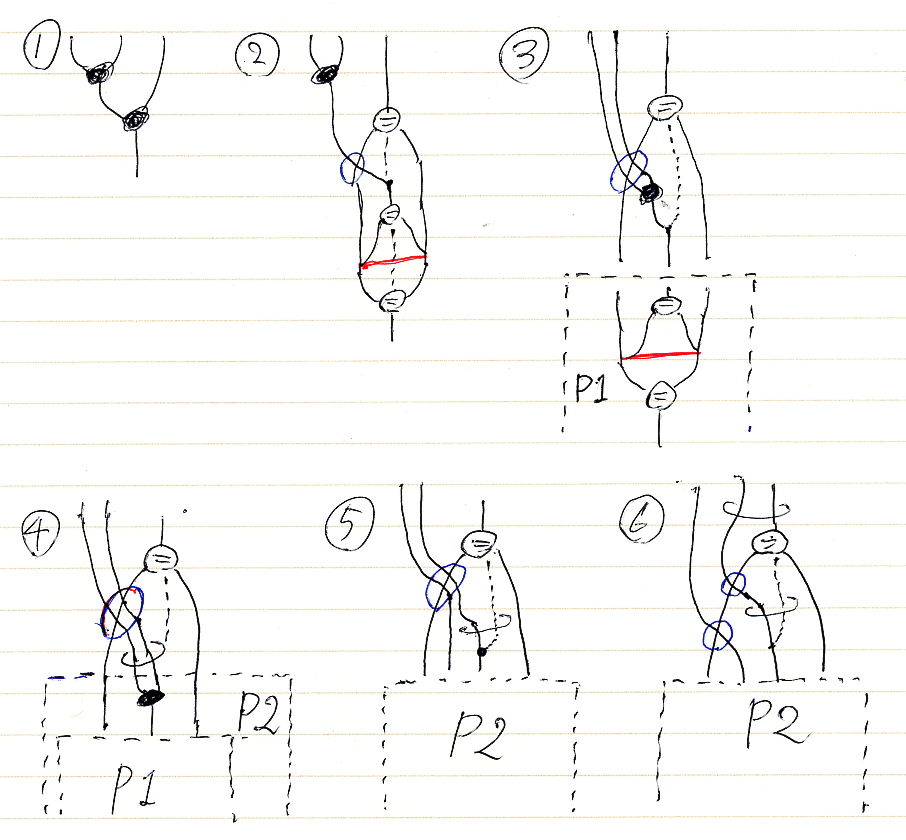
図6'から図9'
各変形ステップについては、項6'から項9'の説明(コメント)を参照してください。P3は、マクロです。
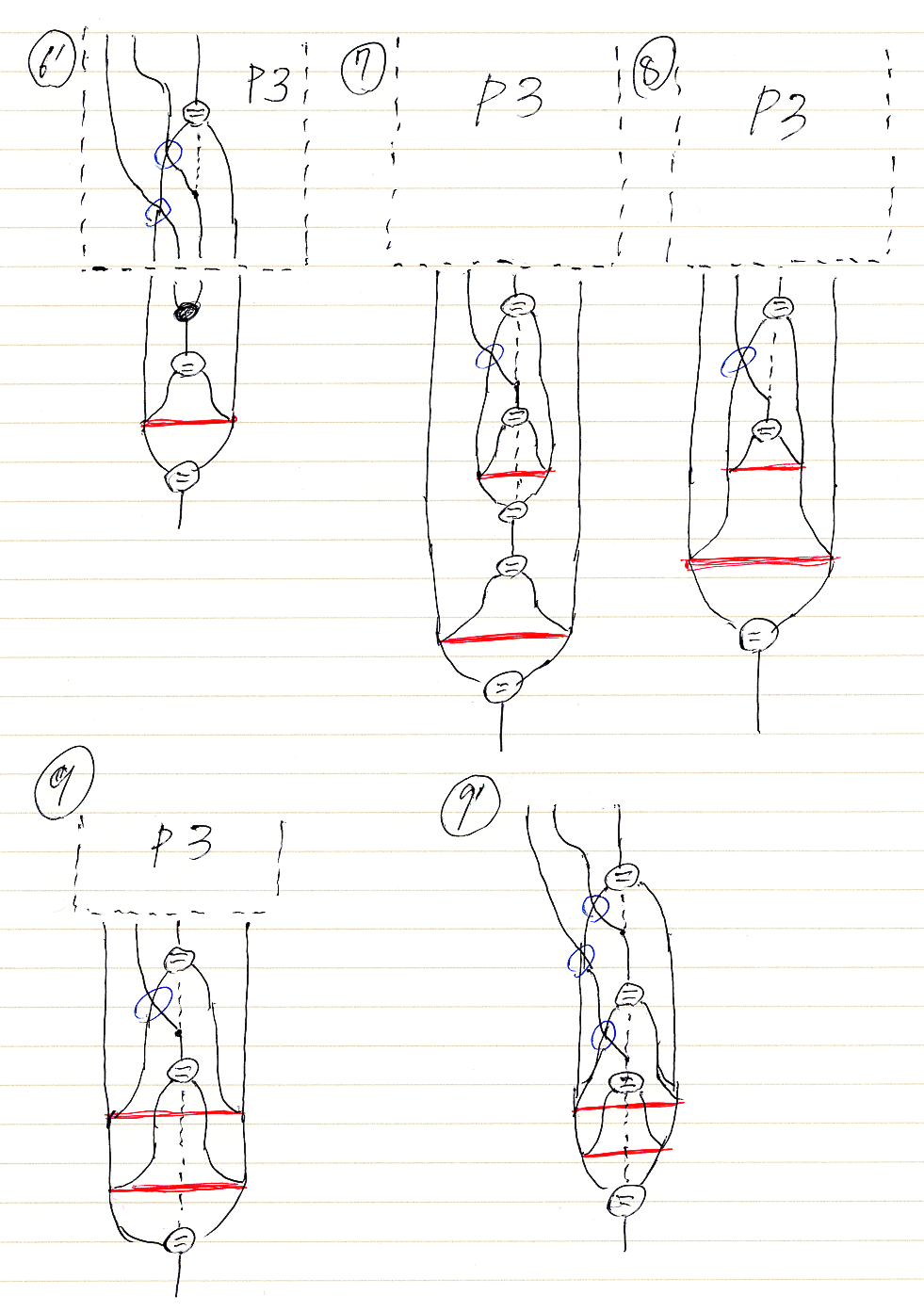
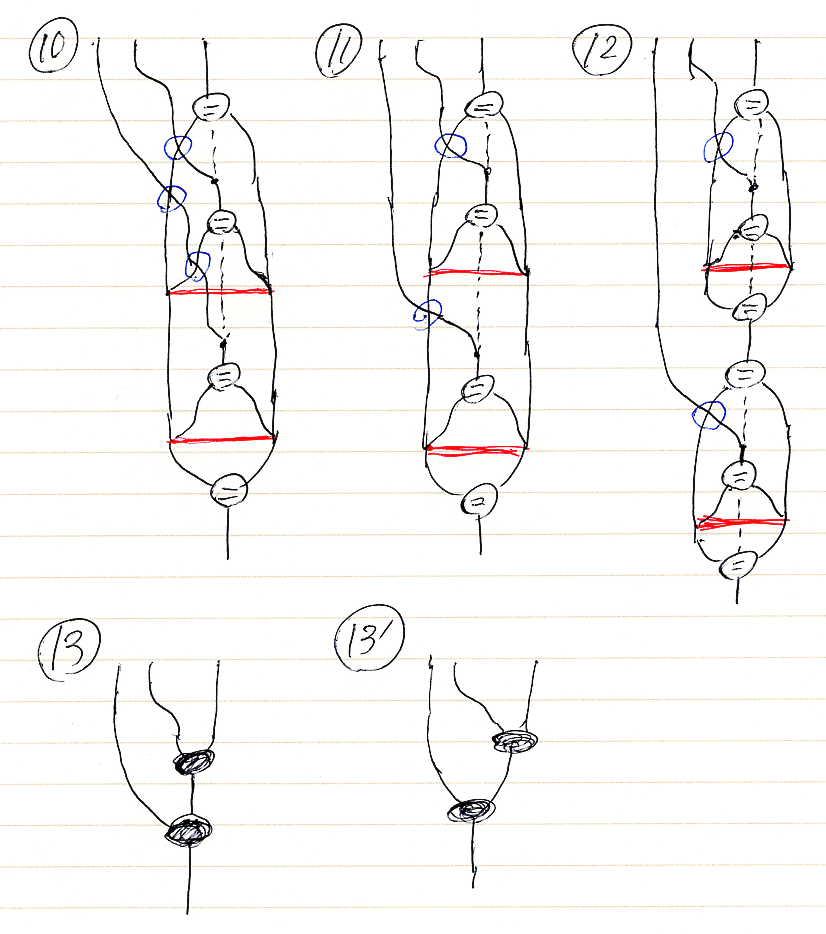
図10から図13'
各変形ステップについては、項10から項13の説明(コメント)を参照してください。図13'は、レイアウトをわずかに変更しただけです。
*1:東日本の地域により(どこの地域かはよく分からない)使われる方言。「放置しておく」「無視して放任する」などの意味。