絵算のテキスト表現（結論：疲れる） - 檜山正幸のキマイラ飼育記 (はてなBlog)

昨日、新しい絵算手法について述べたのですが、絵算の困るところは、適切な描画ツールがない、絵をテキストにシリアライズ／エンコードする方法とデータ交換形式〈data interchange format〉がないことです。“絵”と“絵の変形過程”をテキスト表現できれば、コミュニケーションのコストが劇的に下がります。

そうはいっても、テキスト・エンコード形式を提案したところで普及するような状況ではないので、既存の数式組版（＝TeX）でテキスト表現できないか試してみます。

内容：

ほんとに困っている
例題：モナドから作るモノイド
図式順・反図式順混合記法と行列記法
計算してみる（が、疲れた）

ほんとに困っている

絵算の絵を描く適当なツールはないと思います。Globularは、お絵描きに使えるほどの描画能力は持ってない*1し、ストライプ図をまったくサポートしていません。次のような絵（マースデンとマッカーディ）は、通常の（汎用の）お描きツールで描いていると思われます。

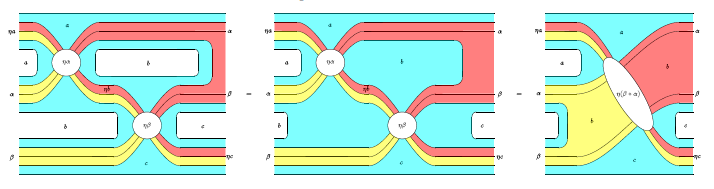
僕は手描きの絵をスキャンしてますが、汚いし、編集して再利用が出来ないのが難点です。

テキスト表現では記述や計算が困難なので絵図を使っているわけで、それをテキストにしても嬉しいことはないのですが、編集と交換の容易性を重視するなら、「なにかしらのテキストで」となるでしょう。また、「どうしても絵図には馴染めない」という人とのコミュニケーション手段としてもテキスト表現が必要です。

こんな困った状況や、妥協的代替手段が必要となるのは、今が過渡期だからだと思います。

例題：モナドから作るモノイド

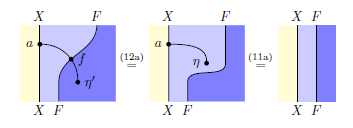
昨日の記事「新しい絵算手法：ストリング＋ストライプ図」で、下のような絵等式〈pictorial equation〉は、「しばらく眺めていると」分かると言いました。実際、数個の変形ルールに慣れれば、等式の絵証明〈pictorial proof〉は難しくはありません。

上記の絵等式の意味は、モノイドの結合律ですが、次の主張の一部となっています。

モノイド圏 C = (C, $\otimes$ , I, α, λ, ρ) 上の強モナド F = (F, μ, η, τ) があると、N = F(I) を台対象とするモノイド N = (N, m, e) を構成可能である。

図式順・反図式順混合記法と行列記法

テキスト表現に際して、図式順・反図式順混合記法を使うので、次の記事の演算子一覧表を見ておいてください。

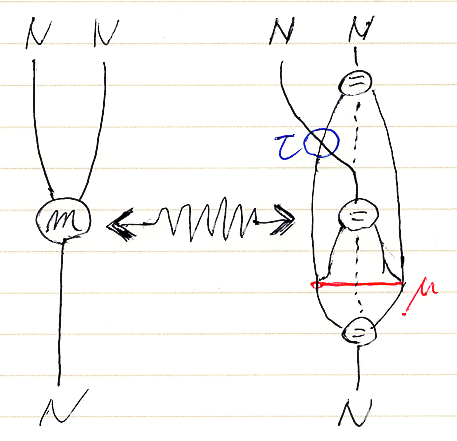
関手と自然変換の計算に出てくる演算子記号とか // 今後使う予定の演算子記号

まず、N = F(I) と置きますが、これは明示的等号ノードで描きます。

関手Fを表すストライプ〈関手シース〉は、色鉛筆で薄く塗りつぶしていたのですが、今日は無色です（面倒だから）。色付きの絵と見比べれば、どこが関手か判断できるでしょう。

モノイドの乗法 m:N $\otimes$ N→N は次のように定義されます。

m := τ_N,I;F(ρ_N);μ_I

これは、図式順・反図式順混合記法です。混合記法が、ストリング＋ストライプ図と相性がいいようです。完全な反図式順記法だと：

m := μ_I $\circ$ F(ρ_N) $\circ$ τ_N,I

完全な図式順記法だと：

m := (N, I).τ ; N.ρ.F ; I.μ

絵算では、この等式を、絵の一部を置換するために使います。

テキスト表現で縦結合（記号は';'または' $\circ$ '）が横並びになるのが辛すぎるので、行列記法で縦（上から下）に並べることにします。

$m \,:=\, \begin{bmatrix} \tau_{N,I} \\ F(\rho_N) \\ \mu_I\end{bmatrix}$

明示的等号ノードも入れて、射のプロファイルも書けば、絵が持っている情報をエンコードできます。

$(m:\,N\otimes N \to N) \,:=\, \begin{bmatrix} N\otimes (N = F(I)):\, N\otimes N \to N\otimes F(I) \\ \tau_{N,I} :\, N\otimes F(I) \to F(N\otimes I) \\ F(\rho_N) :\, F(N\otimes I) \to F(N)\\ F(N = F(I)):\, F(N)\to F(F(I)) \\ \mu_I :\, F(F(I)) \to F(I) \\ F(I) = N :\, F(I)\to N \\ \end{bmatrix}$

レイアウトを工夫すれば、もう少し絵に近くなるかも。

$\begin{bmatrix} & N \otimes N \\ m & \downarrow \\ & N\end{bmatrix}\,:=\,\begin{bmatrix} & N \otimes N \\ N \otimes (N = F(I)) & \downarrow \\ & N \otimes F(I) \\ \tau_{N,I} & \downarrow \\ & F(N \otimes I) \\ F(\rho_N) & \downarrow \\ & F(N) \\ F(N = F(I)) & \downarrow \\ & F(F(I)) \\ \mu_I & \downarrow \\ & F(I) \\ F(I) = N& \downarrow \\ & N \end{bmatrix}$

「写し取ったゾッ！」という達成感はあるものの、疲れますな。この段階でTeXソースは次のよう。

\begin{bmatrix}
 & N \otimes N \\
 m & \downarrow \\
 & N
\end{bmatrix}

\,:=\,

\begin{bmatrix}
 & N \otimes N  \\
 N \otimes (N = F(I)) & \downarrow \\
 & N \otimes F(I) \\
 \tau_{N,I} & \downarrow \\
 & F(N \otimes I) \\
 F(\rho_N) & \downarrow \\
 & F(N) \\
 F(N = F(I)) & \downarrow \\
 & F(F(I)) \\
 \mu_I  & \downarrow \\
 & F(I) \\
 F(I) = N& \downarrow \\
 & N
\end{bmatrix}

誰かが便利パッケージにまとめてくれたりすると楽に書けるかもしれないけど…

計算してみる（が、疲れた）

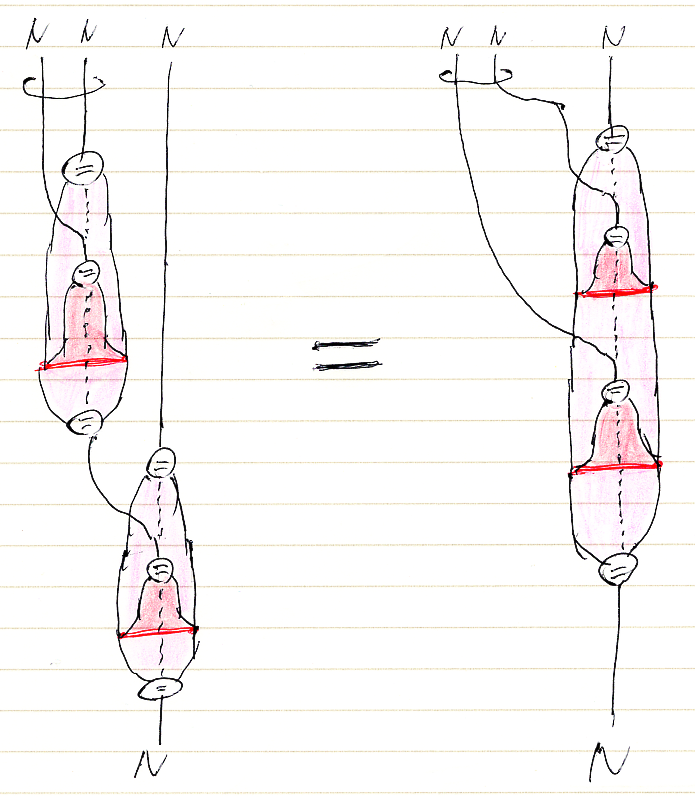
モノイドの結合律を証明する最初のステップは、(m $\otimes$ N);m （Nはid_Nの意味）を図示した初期状態から、左のmをテンソル強度τで関手Fの内部に引っ張り込むことです。絵では次の操作になります。

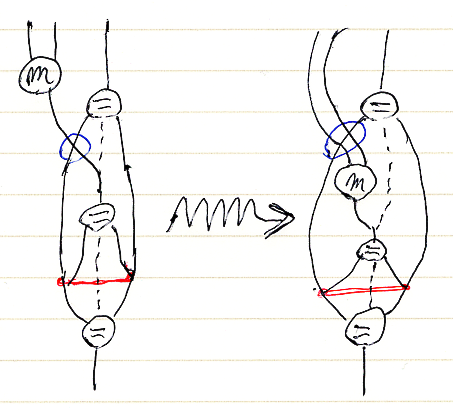
ノードmがストライプ〈関手シース〉内へと貫入〈かんにゅう〉する変形過程ですね。これを行列記法による等式で表しましょう。

$\begin{bmatrix}m\otimes N \\ N\otimes (N = F(I)) \\ \tau_{N,I} \\ F(\rho_N) \\ F(N = F(I)) \\ \mu_I \\F(I) = N \end{bmatrix} \,=\, \begin{bmatrix}(N\otimes N)\otimes (N = F(I)) \\ \tau_{N\otimes N, I} \\ F(m\otimes I)\\ F(\rho_N) \\ F(N = F(I)) \\ \mu_I \\F(I) = N \end{bmatrix}$

実際に変化した部分（上部）と変化してない部分（下部）に分割すると見やすいかも知れません。

$\begin{bmatrix} \begin{bmatrix} m\otimes N \\ N\otimes (N = F(I)) \\ \tau_{N,I} \end{bmatrix} \\ \begin{bmatrix} F(\rho_N) \\ F(N = F(I)) \\ \mu_I \\ F(I) = N \end{bmatrix} \end{bmatrix} \,=\, \begin{bmatrix} \begin{bmatrix} (N\otimes N)\otimes (N = F(I)) \\ \tau_{N\otimes N, I} \\ F(m\otimes I) \end{bmatrix} \\ \begin{bmatrix} F(\rho_N) \\ F(N = F(I)) \\ \mu_I \\F(I) = N \end{bmatrix} \end{bmatrix}$

行列記法を使わないでフラットに書いて、Nをちゃんとid_Nにして、イコール記号による誤解を避けるために、明示的等号ノードをeq_X,Yの形に直して書いてみます。

$( m\otimes id_{N} ; id_{N}\otimes (eq_{N, F(I)}) ; \tau_{N,I} )\,; \\ \:\:\:\: ( F(\rho_N) ; F(eq_{N, F(I)}) ; \mu_I ; eq_{F(I), N} )$
$=$
$( (id_{N}\otimes id_{N})\otimes (eq_{N, F(I)}) ; \tau_{N\otimes N, I} ; F(m\otimes I) )\,; \\ \:\:\:\:( F(\rho_N) ; F(eq_{N, F(I)}) ; \mu_I ; eq_{F(I), N} )$

mを貫入させるだけの操作なんだけど……まったくイメージが湧かない(泣く)

次のステップ -- Fのストライプ内に入ったmを、mの定義に従って展開すると次の絵になります。

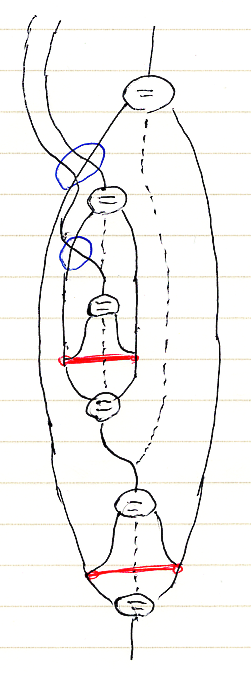
これをテキスト表現すると … …
はぁ、もう気力が続かない。
後で追記で書くかも … しれないけど、
今日はオシマイ。

[追記 date="翌日"]

とりあえず絵を写し取るなら、
$\begin{bmatrix}(N \otimes N)\otimes(N = F(I)) \\\tau_{N\otimes N,I} \\F ( \begin{bmatrix} N \otimes (N = F(I)) \\ \tau_{N, I} \\ F(\rho_{N}) \\ F(N = F(I)) \\ \mu_{I} \\ (F(I) = N) \end{bmatrix} \otimes I ) \\F(\rho_{N}) \\ (N = F(I)) \\\mu_I \\ (F(I) = N)\end{bmatrix}$

これだと情報が少ないので、プロファイルも入れましょう。等号ノードは、横向きの矢印で表すことにします。
$\begin{bmatrix}& (N\otimes N)\otimes N \to (N\otimes N)\otimes F(I) \\\tau_{N\otimes N,I} & \downarrow \\& F( (N\otimes N) \otimes I) \\F ( \begin{bmatrix} & N\otimes N \to N\otimes F(I) \\ \tau_{N, I} & \downarrow \\ & F(N\otimes I) \\ F(\rho_{N}) & \downarrow \\ & F(N) \to F(F(I))\\ \mu_{I} & \downarrow \\ & F(I) \to N \end{bmatrix} \otimes I ) & \downarrow \\& F(N\otimes I) \\F(\rho_{N}) & \downarrow \\& F(N) \to F(F(I)) \\\mu_I & \downarrow \\& F(I) \to N\end{bmatrix}$

左側の入れ子を右に押し込んだほうが見やすいかな。

$\begin{bmatrix}& (N\otimes N)\otimes N \to (N\otimes N)\otimes F(I) \\\tau_{N\otimes N,I} & \downarrow \\& F( (N\otimes N) \otimes I) \\& F ( \begin{bmatrix} & N\otimes N \to N\otimes F(I) \\ \tau_{N, I} & \downarrow \\ & F(N\otimes I) \\ F(\rho_{N}) & \downarrow \\ & F(N) \to F(F(I))\\ \mu_{I} & \downarrow \\ & F(I) \to N \end{bmatrix} \otimes I ) \\& F(N\otimes I) \\F(\rho_{N}) & \downarrow \\& F(N) \to F(F(I)) \\\mu_I & \downarrow \\& F(I) \to N\end{bmatrix}$

最後（三番目）のTeXソースは：

\begin{bmatrix}
& (N\otimes N)\otimes N \to   (N\otimes N)\otimes F(I) \\
\tau_{N\otimes N,I} & \downarrow \\
& F((N\otimes N) \otimes I) \\
& F(
 \begin{bmatrix}
 & N\otimes N \to N\otimes F(I) \\
 \tau_{N, I} & \downarrow \\
 & F(N\otimes I) \\
 F(\rho_{N}) & \downarrow \\
 & F(N) \to F(F(I))\\
 \mu_{I} & \downarrow \\
 & F(I) \to N
 \end{bmatrix}
  \otimes I
)  \\
& F(N\otimes I) \\
F(\rho_{N}) & \downarrow \\
& F(N) \to F(F(I)) \\
\mu_I & \downarrow \\
& F(I) \to N
\end{bmatrix}

[/追記]

*1:Globularはお絵描きツールを意図してません。証明支援系です。使い方の導入は、Globularの使い方 (1)（(1)から(3)まで）などを参照。